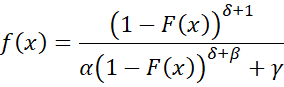Basic Concepts
For 0 ≤ p ≤ 1, the inverse of the Wakeby distribution is defined as
where μ is the location parameter, α, γ are scale parameters and β, δ are shape parameters. These parameters are subject to the following restrictions:
β + δ ≥ 0 α + γ ≥ 0 γ ≥ 0
If β + δ = 0 then β = γ = δ = 0
If γ > 0 then δ > 0
α ≠ 0 or γ≠ 0
The cumulative distribution function (cdf) is the inverse of this function, but it doesn’t have a closed form. The cdf F(x) is defined at x provided
x ≥ μ
Once you have the cdf, you can express the probability density function (pdf) as
Calculating the cdf and pdf
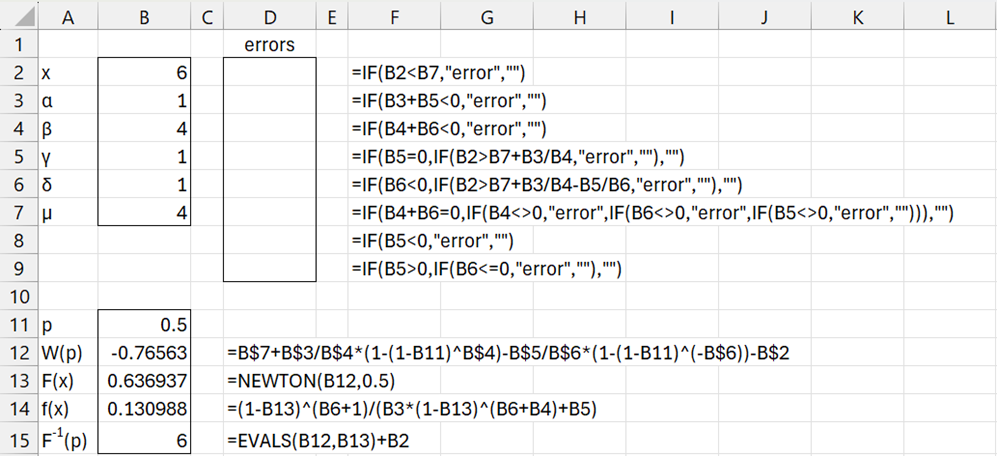
As we observed above, there is no closed form for the cdf. We show how to calculate the cdf at x = 6 for the parameters shown in range B3:B7 of Figure 1.
We do this by finding the value of p that satisfies the equation F-1(p) – x = 0 using Newton’s method (see Root Finding Functions). The left side of this equation is inserted in cell B12 (as shown in cell D12). The Real Statistics formula to estimate p is inserted in cell B13 (as shown in cell D13).
This value of p is F(x). Thus F(6) = .636937, as shown in cell B13. The corresponding pdf value f(6) = .130988, as shown in cell B14. Finally, we check our result by calculating F-1(.636937) = 6, as shown in cell B15.
Figure 1 – Calculating the cdf and pdf
Note that the formulas in range D2:D9 perform error checking based on the restrictions described above.
Worksheet Functions
We can avoid the complicated calculations described above by using Real Statistics capabilities.
Starting with Rel 9.5, the Real Statistics Resource Pack will support the following functions:
WAKEBY_DIST(x, μ, α, β, γ, δ, cum) = the pdf of the Wakeby distribution f(x) when cum = FALSE and the corresponding cumulative distribution function F(x) when cum = TRUE.
WAKEBY_INV(p, μ, α, β, γ, δ) = the inverse of the Wakeby distribution at p
You can obtain the same results as those shown in cells B13, B14, and B15 using the formulas
=WAKEBY_DIST(B2,B7,B3,B4,B5,B6,TRUE)
=WAKEBY_DIST(B2,B7,B3,B4,B5,B6,FALSE)
=WAKEBY_INV(B13,B7,B3,B4,B5,B6)
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Wikipedia (2025) Wakeby distribution
https://en.wikipedia.org/wiki/Wakeby_distribution
Sadiq, N. (2025) Wakeby distribution modelling of rainfall and thunderstorm over northern areas of Pakistan
https://ppaspk.org/index.php/PPAS-B/article/view/320/264