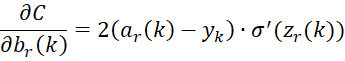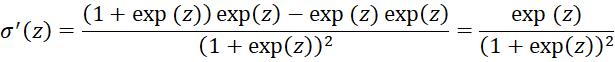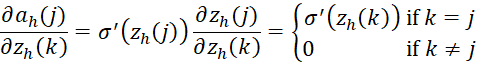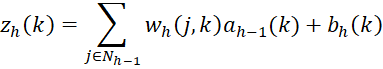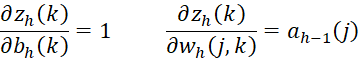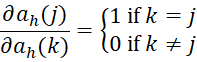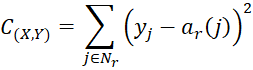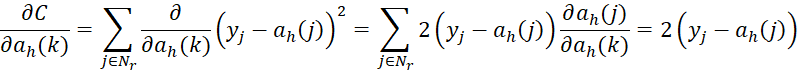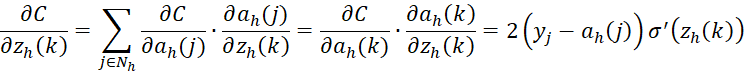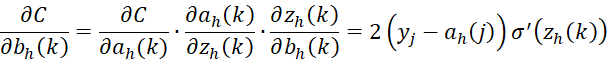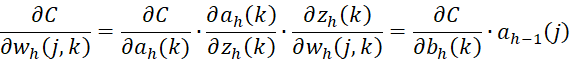Those of you who are familiar with calculus recognize that the backward propagation equalities described in Neural Network Training involve partial derivatives, and so we can actually prove these equalities. For those of you who are not familiar with calculus or don’t care to see the proof, you can skip the following since it is not essential to understanding the functioning of the neural network.
Properties
For r = the Output Layer
For 1 < h < r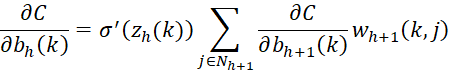
For any h > 1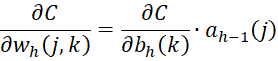
Proof
As we see in Neural Network Basic Concepts
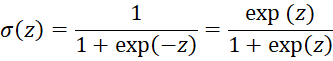
Applying the quotient rule, we get
Since
as we see in Neural Network Basic Concepts, it follows that
Again from Neural Network Basic Concepts, we know that
from which it follows that
Also
Finally, from Neural Network Basic Concepts
from which it follows that (dropping the subscript on C and using h = r)
By the chain rule and using the above observations, we get
Using the chain rule one more time, we get
where h = r. The following also follows for any h > 1.
The equation
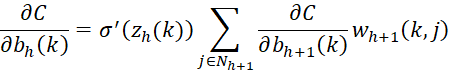
where h < r is proved in a similar manner using the chain rule.