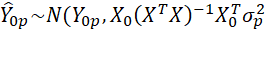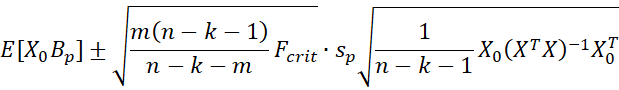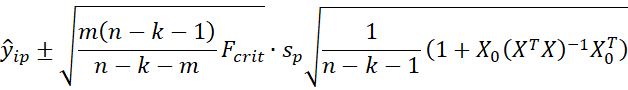Objective
On this webpage we describe how to make predictions based on a multivariate regression model. We also provide properties of these predictions and estimate prediction intervals.
Basic Concepts
Definition 1: Suppose we have a multivariate regression model with coefficients B built from the training data in in the n × k matrix X and n × m matrix Y. Further, suppose we have a 1 × (k+1) row vector X0 = [1, x1, …, xk]. Then the prediction at X0 is the 1 × m vector Ŷ0 where
The columns of the prediction, therefore, satisfy
Property 1:
Proof: By Property 1 of Multivariate Regression Basic Concepts
Property 2:
where dfRes = n – k – 1
Proof: By Property 1
where the last equality results from Property 5 of Multivariate Regression Basic Concepts.
Property 3: If the normality assumption holds for the multivariate regression model, then
Proof: This follows from Properties 1 and 2.
Property 4:
Proof:
where the last equality results from Property 5 of Multivariate Regression Basic Concepts.
Confidence Intervals
Assuming normality, a simultaneous 1-α confidence interval for E[X0Bp] is given by
or equivalently
where
Prediction Intervals
Assuming normality, a simultaneous 1-α prediction interval is given by
Or equivalently
Worksheet Functions
The Real Statistics Resource Pack provides the following two worksheet functions where R0 is a t × k array, Rx is an n × k array, Ry is an n × m array, and Rc is a k × m array.
MRegPred(R0, Rx, Ry): returns a column array with the predictions of the Y values for the X values in R0 using the multivariate regression model based on the data in Rx and Ry
MRegPredC(R0, Rc): returns a column array with the predictions of the Y values for the X values in R0 using the multivariate regression model based on the coefficients in Rc
References
Johnson, R. A., Wichern, D. W. (2007) Applied multivariate statistical analysis. 6th Ed. Pearson
https://mathematics.foi.hr/Applied%20Multivariate%20Statistical%20Analysis%20by%20Johnson%20and%20Wichern.pdf
Rencher, A.C., Christensen, W. F. (2012) Methods of multivariate analysis (3nd Ed). Wiley
Helwig, N. E. (2017) Multivariate linear regression
http://users.stat.umn.edu/~helwig/notes/mvlr-Notes.pdf