Friedman-Rafsky Test

Basic Concepts

The Friedman-Rafsky test is a multivariate version of the Wald-Wolfowitz runs test.

Assume that we have two sets of k-tuples X and Y of sizes n₁ and n₂ drawn from populations with cumulative distribution functions F_X and F_Y. We test the null hypothesis that F_X = F_Y.

Univariate Runs Test

The univariate test (where k = 1) consists of sorting the elements from X combined with Y and counting the number of runs r of either 1’s or 2’s where each element of X is replaced by a 1 and each member of Y is replaced by a 2. The null hypothesis is equivalent to the order of the 1’s and 2’s is random. This can be tested for n = n₁ + n₂ large enough (approximately > 20) based on the null hypothesis H₀  has an approximately normal distribution N(μ, σ²) where

This is equivalent to z has a standard normal distribution where z = (μ–r)/σ.

Multivariate Runs Test

For the multivariate case, we need to replace the notion of a sorted list of elements from X union Y by a minimal spanning tree (MST) as described in Graph Theory. More specifically, we consider the undirected graph whose nodes (vertices) are the n elements in X union Y. The edges are all the C(n,2) pairs of elements from X union Y. We actually consider a weighted graph where the weight for each edge is the Euclidean distance between the nodes in the edge.

Note that MST is a subset of all the edges characterized by: (1) every node is contained in at least one edge in the MST, (2) the MST is a tree, i.e. it is a connected graph (i.e. there is a path in the MST between any two nodes) and there is no cycle (i.e. there is no path that starts and ends with the same node) and (3) the sum of the weights in the MST is minimum.

The number of runs r is equal to the number of disjointed trees that result when any edge in the MST between nodes from different samples is removed. When k = 1 the number of runs r is equivalent to that in the Wald-Wolfowitz test.

The Friedman-Rafsky test statistic is similar to that used for the Wald-Wolfowitz test, namely

where

and c = the number of edge pairs that share a common node, which can be calculated by

where d_i = the degree of node i in the MST, i.e. the number of edges connected to node i.

Note that when p = 1, c = n–2 and so σ² is as for the Wald-Wolfowitz test.

Example

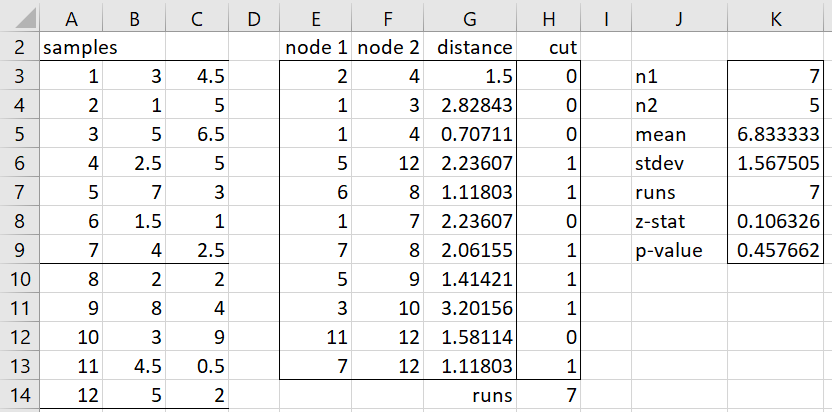
Example 1: Determine whether the samples of points in ranges B3:C9 and B10:B14 of Figure 1 come from populations with the same distribution using the Friedman-Rafsky test.

Figure 1 – Friedman-Rafsky Test

The results of the test are shown on the right side of Figure 1, where the array formula =FR_Test(B3:C9,B10:C14,TRUE) is used to obtain the results of the Friedman-Rafsky test. Since p-value = .45 > .05 = alpha, we conclude that there is not sufficient evidence to rule out that the samples come from the same population. Since the samples are quite small, the number of runs (cell K7) would have to be much higher or much lower in order to obtain a significant result.

Note that we can also obtain the number of runs directly from the minimum spanning tree, as shown in the middle of Figure 1. The values in range E3:G13 are obtained from the array formula =MSTVectors(B3:C14) (see MST for r-tuples). We need to count the number of edges that connect nodes from two different samples. This is done by placing the formula =IF(E3<=7,IF(F3>7,1,0),IF(F3<=7,1,0)) in cell H3, highlighting the range H3:H13 and pressing Ctrl-D. The number of runs, 7, is obtained via the formula =SUM(H3:H13)+1 in cell H14.

References

Friedman, J. H. and Rafsky, L. (1979) Multivariate generalizations of the Wald-Wolfowitz and Smirnov two-sample tests. The annals of statistics, Vol. 7. No. 4
https://projecteuclid.org/euclid.aos/1176344722

Smith, S. P. and Jain, A. K. (1988) A test to determine the multivariate normality of a data set. IEEE transactions on pattern analysis and machine intelligence, Vol.10. No. 5.
https://www.semanticscholar.org/paper/A-Test-to-Determine-the-Multivariate-Normality-of-a-Smith-Jain/838bf260f222a7edec199750973daefe7fb0bf52