Basic Concepts
In Discriminant Analysis, given a finite number of categories (considered to be populations), we want to determine which category a specific data vector belongs to. More specifically, we assume that we have r populations D1, …, Dr consisting of k × 1 vectors. Furthermore, we assume that each population has a multivariate normal distribution N(μi,Σi). The values for μi and Σi are estimated using training data for which we know which population Di each X in the training data belongs to.
For each i let fi(X) be the pdf for N(μi,Σi), and so we can define f(X|Di) = fi(X).
In Linear Discriminant Analysis we assume that Σ1 = Σ2 = … = Σr = Σ, and so each Di is differentiated by the mean vector μi.
Bayesian Approach
We use a Bayesian analysis approach based on the maximum likelihood function. In particular, we assume some prior probability function
We can then define a posterior probability function
For each X we decide which population X belongs to based on maximizing the value of pi(X). Since for any i the denominator in the expression for pi(X) is the same (and positive), this is equivalent to maximizing the numerator, i.e. X ∈ Di* where
It now follows that
Since this first term is the same for each i, it can be dropped as it won’t affect the value of i*. This motivates the following definitions.
We now define the linear discriminant function to be
where![]()
![]()
and di0(X) = di0 and dij(X) = dij.
We also define the linear score to be si(X) = di(X) + LN(πi). As we demonstrated above, i* is the i with the maximum linear score.
Using the training data, we estimate the value of μi by the mean of the Xi = the average of all the training data in Di. Similarly, we estimate the value of Σ by the pooled sample covariance matrix S. More precisely, let Si be the covariance matrix for Di, then the pooled covariance matrix is
where ni = the number of elements in Di. Thus, we estimate the various linear scores using
![]()
We can assign the prior probability functions πi(X) based on our best available prior information, as long as πi(X) = 1 and πi(X) > 0 for all i.
In particular, if we assume that all populations are equally likely then we can choose
If we assume that the probability is weighted by the population size then
The posterior probability that is given by the formula
Examples
Example 1: Perform discriminant analysis on the data in Example 1 of MANOVA Basic Concepts. This data is repeated in Figure 1 (in two columns for easier readability). Also determine in which category to put the vector X with yield 60, water 25 and herbicide 6.
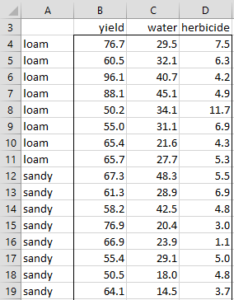 |
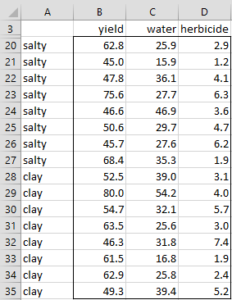 |
Figure 1 – Training Data for Example 1
Assumptions
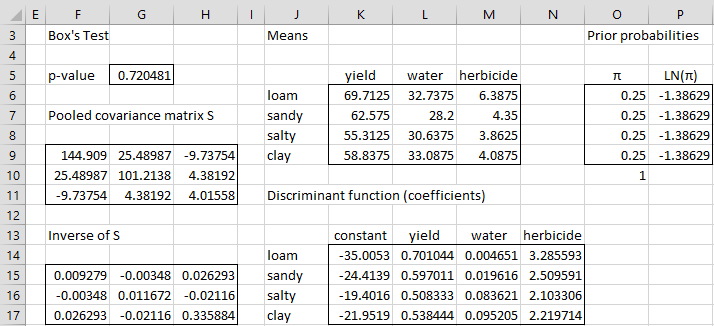
The analysis begins as shown in Figure 2. First, we perform Box’s M test using the Real Statistics formula =BOXTEST(A4:D35). Since p-value = .72 (cell G5), the equal covariance matrix assumption for linear discriminant analysis is satisfied. The other assumptions can be tested as shown in MANOVA Assumptions.
Pooled covariance and mean vectors
We next calculate the pooled covariance matrix (range F9:H11) using the Real Statistics array formula =COVPooled(A4:D35). The inverse of this matrix is shown in range F15:H17, as calculated by the Excel array formula =MINVERSE(F9:H11).
The mean vector for the loam population is displayed in range K6:M6, with the mean vectors for the other three populations shown just below it. These values are calculated by putting the formula
=AVERAGEIF($A$4:$A$35,$J6,B$4:B$35)
in cell K6, highlighting the range K6:M9 and pressing Ctrl-R and Ctrl-D.
Figure 2 – Discriminant Analysis
We will assume that a prior all four categories are equally likely and so we set the prior probabilities to 25% as shown in range O6:O9. The LN for each of these values is shown in range P6:P9.
Discriminant analysis coefficients
Finally, we calculate the coefficients of the discriminant analysis in range K14:N17. Here, K14 contains the value of d10, as calculated by the array formula
=-0.5*MMULT(K6:M6,MMULT($F$15:$H$17,TRANSPOSE(K6:M6)))
The remaining d1j coefficients (for loam) are calculated by inserting the following array formula in range L14:N14
=MMULT(K6:M6,$F$15:$H$17)
Highlighting the range K14:N17 and pressing Ctrl-D, we fill in the dij coefficients for the other three categories.
Best category
We now determine in which category to put the vector X with yield 60, water 25 and herbicide 6 (see Figure 3).
Figure 3 – Determining the best category
First, we determine the score for each category i using the formula
For example, the score for loam is 25.50092, as calculated using the formula
=$K$14+SUMPRODUCT(S38:U38,$L$14:$N$14)+$P$6
The scores for the other three categories are calculated in a similar manner using the discriminant coefficients and prior probability. We see that the score for sandy is the highest and so we use that as the category for X (cell Z38). Note that this category can be determined by the following formula:
=INDEX($V$3:$Y$3,,MATCH(MAX(V38:Y38),V38:Y38,0))
The posterior probability that X is in the loam population is shown in cell V39, as calculated by the formula
=EXP(V$38)/SUMPRODUCT(EXP($V$38:$Y$38))
which is 35.2%. There is a 37.6% probability that it will be classified as sandy (cell W39), and so we are only 37.6% confident that X is in the sandy population (i.e. a 62.4% error rate). Whether this is a sufficiently high level of confidence depends on the cost of being wrong and the reward for being right. If we are predicting which women have cancer based on a mammogram, we would clearly require a much higher level of confidence.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
Penn State (2017) Linear discriminant analysis. STAT 505 Applied Multivariate Statistical Analysis
https://online.stat.psu.edu/stat505/lesson/10/10.3
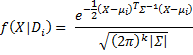
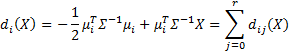

Hello – I am trying to set up my data to perform LDA and have been using your example as a template. I can’t for the life of me get it to accept my input – I keep getting an ‘invalid training set’ error message. Are you able to provide any guidance on what might be causing this? I was able to select the example data set and perform it fine. Thanks!
Hello Darren,
If you email me an Excel spreadsheet with your data and specify how you filled in the dialog box, I will try to figure out why you are getting this error.
Charles
hola, podria colocar el procedimiento utilizado en excel para ejecutar este analisis?…por favor.
Which analysis are you referring to? The Real Statistics software already supports Linear Discriminant Analysis.
Charles
Thanks for the detailed post. I see that you have 4 classes and you have 4 discriminant functions (with intercept) i.e one for each class. However when I try to run the same in a software such as R, I get only 3 discriminant functions (LD1,LD2 and LD3) i.e one less than the number of classes, in which case, could you clarify how is the prediction done?
Hello Sendil,
In Example 1 on this webpage, you have 4 categories: loan, sandy, salty, clay. Are you saying that R removes one of these categories? That would be strange.
In your question, what do LD1, LD2 and LD3 refer to?
Charles
I’m working with 3 different places, each with 10 tracks. I have variables to evaluate the length of the trail and the number of vertebrates depending on each place. I would like to know the right way or model to assemble the spreadsheet to be executed in the softwere r
Dear Charles
I am geologist
I want using Real-statistics for population discrimination of grain size.
My samples represent the size range with % for each range. How can I identify the populations composed each sample?
example : this is the grain size analysis of one sample
size (mm) %
>0.04 11.22
0.04 16.55
0.05 16.52
0.06 20.5
0.08 16.29
0.10 70.82
0.13 101.34
0.16 79.5
0.20 45.92
0.25 26.04
0.32 21.53
0.40 17.16
0.50 13.32
0.63 9.24
0.80 10.96
1.00 20.33
2.00 2.48
Best regards
Sorry, but I don’t understand your question nor what the data represents.
Charles
Dear Charles
In my work, I did a granulometric analysis of soil samples.
Each sample is sieved through a series of sieves (ranging from 0.4 mm to 2 mm). The particle size fractions obtained for each class will be weighed: each particle size fraction of a given weight (Pi) corresponds to class size (in mm).
the problem that the sample is composed by a mixture of granulometric subpopulations
the sieving data are presented in the form of a statistical series composed of classes with the corresponding weight in%
class (mm) ———————– weight ( Pi %)
> 0.4 ————————- 11.22
[0.04 – 0.05 [——————— 16.55
[0.05 – 0.06 [——————— 16.52
[0.06 – 0.08 [——————— 20.5
[0.08 – 0.10 [——————— 16.29
[0.10 – 0.13 [——————— 70.82
[0.13 – 0.16 [——————— 101.34
[0.16 – 0.20 [——————— 79.5
[0.20 – 0.25 [——————— 45.92
[0.25 – 0.32 [——————— 26.04
[0.32 – 0.40 [——————— 21.53
[0.40 – 0.50 [——————— 17.16
[0.50 – 0.63 [——————— 13.32
[0.63 – 0.80 [——————— 9.24
[0.80 – 1.00 [——————— 10.96
[1.00 – 2.00 [——————— 20.33
<2 ————————- 2.48
the question is how can I determine or discriminate granular subpopulation from its data?
Thank you in advance for your passion
Best regards
Hello Mohamed,
On what basis will you define sub-populations? For discrimination analysis you already have the categories and you want to fit new data into those categories. Here, you need to first define the categories. This can be done in many ways.
Charles
How do I acquire these functions in EXCEL?
Is there a free add-in that I can download or is it a software package that I have to purchase?
Kenneth,
These functions are not available in Excel.
These functions are available for free from the Real Statistics Resource Pack. See
https://real-statistics.com/free-download/real-statistics-resource-pack/
Charles
I have a doubt, the equation to determine coefficient of discriminant analysis looks like a gaussian mixture model, is there any difference of them?
There are a number of websites that address this issue. See, for example:
https://stats.stackexchange.com/questions/254963/differences-linear-discriminant-analysis-and-gaussian-mixture-model
https://www.jstor.org/stable/pdf/2346171.pdf?seq=1#page_scan_tab_contents
Charles
How do we get the values for LN that is shown in range P6:P9?
oh, i just noticed it means the natural log, i thought it’s something else.