Ridge Regression Example

Example

Example 1: Find the linear regression coefficients for the data in range A1:E19 of Figure 1.

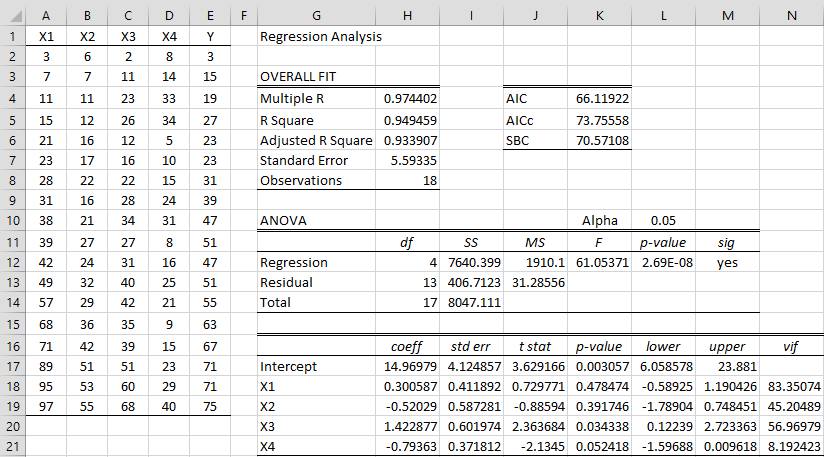
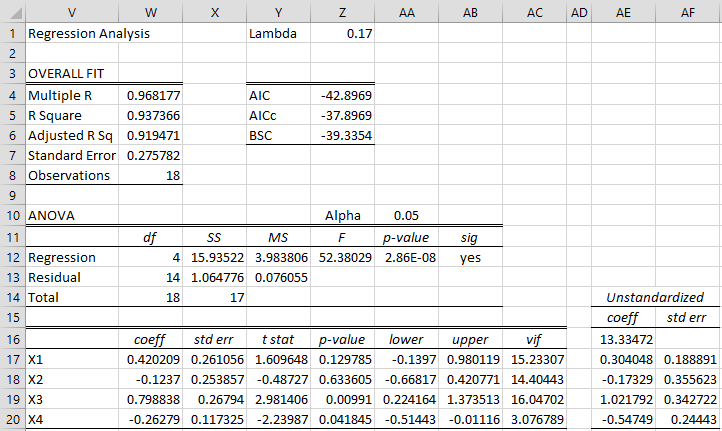
Figure 1 – OLS linear regression

We start by using the Multiple Linear Regression data analysis tool to calculate the OLS linear regression coefficients, as shown on the right side of Figure 1. Note that the standard error of each of the coefficients is quite high compared to the estimated value of the coefficient, which results in fairly wide confidence intervals.

Also note that VIF values for the first three independent variables are much bigger than 10, an indication of multicollinearity. This is confirmed by the correlation matrix displayed in Figure 2.

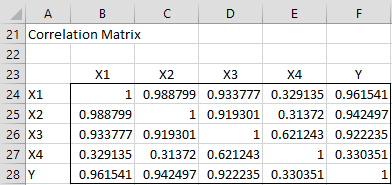
Figure 2 – Correlation matrix

We see that the correlation between X1 and X2 is close to 1, as are the correlations between X1 and X3 and X2 and X3.

Ridge Regression Version

We repeat the analysis using Ridge regression, taking an arbitrary value for lambda of .01 times n-1 where n = the number of sample elements; thus, λ = .17. First, we need to standardize all the data values, as shown in Figure 3.

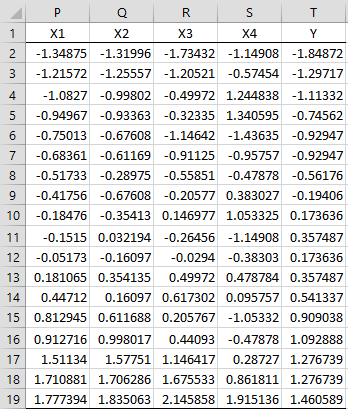
Figure 3 – Standardization of input data

The values in each column can be standardized using the STANDARDIZE function. E.g. range P2:P19 can be calculated by placing the following array formula in the range P6:P23 and pressing Ctrl-Shft-Enter:

=STANDARDIZE(A2:A19,AVERAGE(A2:A19),STDEV.S(A2:A19))

If you then highlight range P6:T23 and press Ctrl-R, you will get the desired result. Alternatively, you can place the Real Statistics array formula =STDCOL(A2:E19) in P2:T19, as described in Standardized Regression Coefficients.

Changing the lambda value

To create the Ridge regression model for say lambda = .17, we first calculate the matrices X^TX and (X^TX + λI)^–1, as shown in Figure 4.

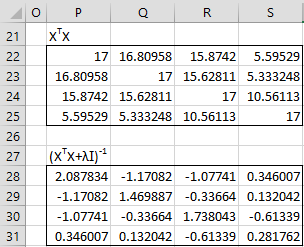
Figure 4 – Selected matrices

X^TX in P22:S25 is calculated by the worksheet array formula =MMULT(TRANSPOSE(P2:S19),P2:S19), and  in range P28:S31 by the array formula =MINVERSE(P22:S25+Z1*IDENTITY()) where cell Z1 contains the lambda value .17.

Next, we use the Multiple Linear Regression data analysis tool on the X data in range P6:S23 and Y data in T6:T23, turning the Include constant term (intercept) option off and directing the output to start at cell V1. Now make the following modifications:

Highlight the range W17:X20 and press the Delete key to remove the calculated regression coefficient and their standard errors.

Calculating the coefficients, standard errors, SSE, VIF

Calculate the correct Ridge regression coefficients by placing the following array formula in the range W17:W20:

=MMULT(P28:S31,MMULT(TRANSPOSE(P2:S19),T2:T19))

Calculate the standard errors by placing the following array formula in range X17:X20:

=W7*SQRT(DIAG(MMULT(P28:S31,MMULT(P22:S25,P28:S31))))

We also modify the SSE value in cell X13 by the following array formula:

=SUMSQ(T2:T19-MMULT(P2:S19,W17:W20))+Z1*SUMSQ(W17:W20)

and place the formula =X14-X13 in cell X12.

Finally, we modify the VIF values by placing the following formula in range AC7:AC20:

=(W8-1)*DIAG(MMULT(P28:S31,MMULT(P22:S25,P28:S31)))

After all these modifications we get the results shown on the left side of Figure 5.

Figure 5 – Ridge Regression

The ordinary regression coefficients and their standard errors, as shown in range AE16:AF20, can be calculated from the standard regression coefficients using the array formula

=UnStdRegCoeff(A2:D19,E2:E19,W17:X20)

as described in Standardized Regression Coefficients.

Worksheet Functions

Real Statistics Functions: The Real Statistics Resource Pack provides the following functions that simplify some of the above calculations.

RidgeRegCoeff(Rx, Ry, lambda, std) – returns an array with standardized Ridge regression coefficients and their standard errors for the Ridge regression model based on the x values in Rx, y values in Ry, and designated lambda value. If std = TRUE, then the values in Rx and Ry have already been standardized; if std = FALSE (default) then the values have not been standardized. Note that the output contains two columns, one for the coefficients and the other for the corresponding standard errors, and the same number of rows as Rx has columns.

RidgeCoeff(Rx, Ry, lambda) – returns an array with unstandardized Ridge regression coefficients and their standard errors for the Ridge regression model based on the x values in Rx, y values in Ry, and designated lambda value. Note that the output contains two columns, one for the coefficients and the other for the corresponding standard errors, and the same number of rows as Rx has columns plus one (for the intercept). The values in Rx and Ry are not standardized.

RidgeVIF(Rx, lambda) – returns a column array with the VIF values using a Ridge regression model based on the x values in Rx and the designated lambda value. Note that the output will be the same whether or not the values in Rx have been standardized.

RidgeRSQ(Rx, Rc, std) – returns the R-square value for Ridge regression model based on the x values in Rx and standardized Ridge regression coefficients in Rc. If std = TRUE, then the values in Rx have already been standardized; if std = FALSE (default) then the values have not been standardized.

Examples

The array formula RidgeRegCoeff(A2:D19,E2:E19,.17) returns the values shown in W17:X20.

RidgeCoeff(A2:D19,E2:E19,.17) returns the values shown in AE16:AF20.

RidgeVIF(A2:D19,.17) returns the values shown in range AC17:AC20.

RidgeRSQ(A2:D19,W17:W20) returns the value shown in cell W5.

References

bquanttrading (2015) Ridge regression in Excel/VBA
https://asmquantmacro.com/2015/12/11/ridge-regression-in-excelvba/

Marquardt, D. W. and Snee, R. D. (1975) Ridge regression in practice. The American Statistician
https://www.jarad.me/stat615/papers/Ridge_Regression_in_Practice.pdf

PennState (2018) Ridge regression. Applied Data Mining and Statistical Learning
https://online.stat.psu.edu/stat857/node/155/