Permutation Matrix
A permutation matrix is a square matrix that has exactly one non-zero element in each row and each column, and the only permissible nonzero element is one.
This type of matrix captures the row permutations that are used in Gaussian elimination (see Systems of Linear Equations)
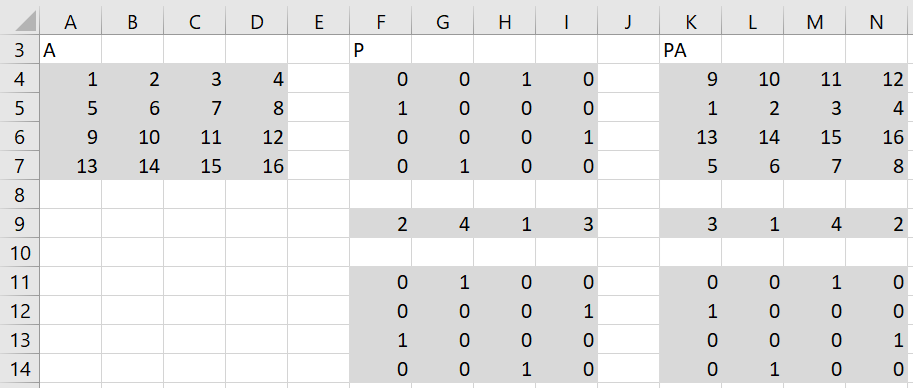
Example 1: The permutation matrix P in F4:I7 of Figure 1 transforms the square matrix A in range A4:D7 to the PA matrix in K4:N7 via the formula =MMULT(F4:I7,A4:D7).
Figure 1 – Permutation matrix
The permutation matrix can be interpreted as follows. The one in the first column of P is in the second row, which indicates that the first row in A will become the second row in PA. Similarly, the one in the second column of P occurs in the fourth row, which indicates that the second row of A becomes the fourth row of PA, etc. Here, the row vector F9:I9 summarizes these permutations.
The inverse transformation which transforms the PA matrix to A is simply PT, which is equal to P-1, and so PT(PA) = P-1(PA) = A. For Example 1, PT is shown in F11:I14.
Worksheet Function
Real Statistics Function: The Real Statistics Resource Pack contains the following array function that produces PT from the row matrix of the type shown in range F9:I9.
MPERM(R1): outputs the permutation matrix defined by the permutations listed in the row array R1. E.g. if R1 contains the values 4, 1, 3, 2 then the output will be a 4 × 4 matrix whose only non-zero entries are ones in the 4th column of row 1, the 1st column of row 2, the 3rd column of row 3 and the 2nd column of row 4.
For Example 1, the formula =MPERM(F9:I9) returns the permutation matrix shown in range F11:I14.
LUP Decomposition
A LU factorization (or LU decomposition) of a square matrix A consists of an upper triangular matrix U, a lower diagonal matrix L, and a permutation matrix such that PA = LU. We also refer to this as an LUP factorization or LUP decomposition.
Property 1 (LU Factorization): For any square matrix A, we can construct an LUP factorization.
Proof: The LUP factorization can be constructed using the Gaussian elimination procedure described in Systems of Linear Equations.
LU Worksheet Functions
Real Statistics Functions: The Real Statistics Resource Pack contains the following array functions that return the LU factorization of a square matrix.
LUPFactorP(R1): outputs the n × n permutation matrix of the LUP decomposition of the n × n matrix in array R1.
LUPFactorL(R1): outputs the n × n lower triangular matrix of the LUP decomposition of the n × n matrix in array R1.
LUPFactorU(R1): outputs the n × n upper triangular matrix of the LUP decomposition of the n × n matrix in array R1.
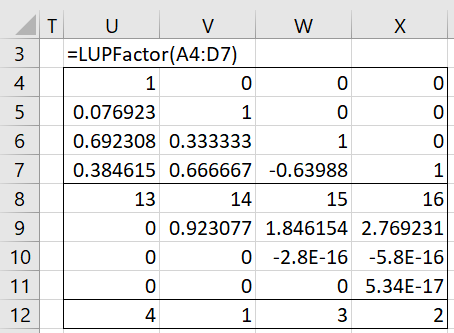
LUPFactor(R1): outputs a 2n+1 × n array consisting of the components of the LUP decomposition of the n × n matrix in array R1. The first n rows of the output consist of a lower triangular matrix L, the next n rows consist of an upper triangular matrix U and the last row defines the permutation of the rows of R1 required to create the matrix P such A = PTLU where A is the matrix in R1.
The Real Statistics Resource Pack also provides the following functions which use the LU decomposition to obtain the determinant and inverse of a square matrix, as well as the solution to a set of linear equations, in a manner similar to that described in Systems of Linear Equations.
LUDet(R1) = the determinant of the square matrix in R1 using the LU decomposition
LUInverse(R1): outputs the inverse of the square matrix in R1 using the LU decomposition
LUSolve(R1, R2): outputs the solution to the series of linear equations AX = C where R1 contains matrix A and R2 contains the column array C; an error value is returned when there is no solution or there is no unique solution
LUP Example
Example 2: Find the LUP factorization of matrix A from Example 1.
Figure 2 – LUPFactor function
Data Analysis Tool
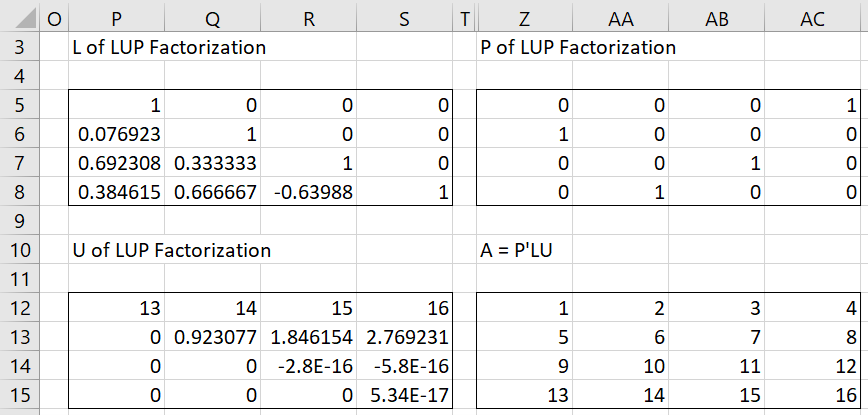
Real Statistics Data Analysis Tool: The Matrix data analysis tool contains an LU Factorization option that computes the LU factorization of the matrix in the Input Range. See Figure 1 of Matrix Operations Tool for how to use this tool.
After clicking on the OK button of the dialog box, the output shown in Figure 3 will appear (reformatted to fit better on the page). As you can see from Z12:AC15, A = PTLU. Note too that range Z5:AC8 can be calculated using the formula =MPERM(U12:X12).
Figure 3 – Output from Matrix Operations analysis tool
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Golub, G. H., Van Loan, C. F. (1996) Matrix computations. 3rd ed. Johns Hopkins University Press
Searle, S. R. (1982) Matrix algebra useful for statistics. Wiley
Perry, W. L. (1988) Elementary linear algebra. McGraw-Hill
Fasshauer, G. (2015) Linear algebra.
https://math.iit.edu/~fass/532_handouts.html
Lambers, J. (2010) Numerical linear algebra
https://www.yumpu.com/en/document/view/41276350