Basic Concepts
Let A be an invertible n × n matrix and let A = QTQT be a Schur’s factorization of A. We now show how to calculate the eigenvectors of A.
Property 1: Suppose that QTQT is a Schur’s factorization of A. If X is an eigenvector of T corresponding to eigenvalue λ, then QX is an eigenvector of A corresponding to λ.
Proof: Assume X is an eigenvector of T corresponding to eigenvalue λ. Then TX = λX, and so AQX = QTQTQX = QTX = QλX = λQX.
Observation: By Property 1, it is sufficient to be able to construct eigenvectors for upper triangular square matrices, which we can do as described in the following property.
Property 2: If λ is an eigenvalue of an invertible upper triangular matrix T, we can construct an eigenvector of T corresponding to λ.
Proof: We start by investigating the characteristics of such an eigenvector. Let X be an eigenvector corresponding to the eigenvalue λ of the upper triangular n × n matrix T. Thus λ = tii for some i, 1 ≤ i ≤ n, and (T−λI)X = O.
Now we express T and X as follows:
where T22 = λ. Thus, (T−λI)X can be expressed as
Since T is invertible and upper triangular, by Property 1c of Eigenvalues and Eigenvectors, none of the values on its main diagonal is zero. Since T11 and T33 are upper triangular (whose diagonals contain elements from the main diagonal of T), if we assume that λ has multiplicity of 1, then T11−λI and T33−λI don’t have any zero values on their main diagonal, and so by Property 1c of Eigenvalues and Eigenvectors, they are invertible.
Finally, since T33−λI is invertible and (T33−λI)X3= O, it follows that X3= O. We set X2 = 1 (X2 is a scalar) since any non-zero value will yield an equivalent result. Thus
and so we conclude that
We have therefore shown how to construct the eigenvector X where
Here, the first block is an i−1 × 1 vector, the second block is the scalar 1, and the third block is the n−i × 1 zero vector.
Example
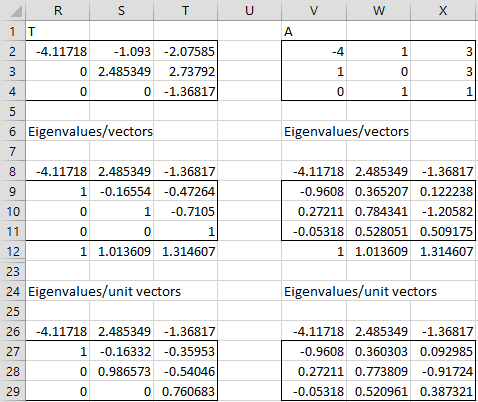
Example 1: Find the eigenvectors for matrix A in range A2:C4 of Figure 1 of Schur’s Factorization (repeated in range V2:X4 of Figure 1 below).
We start by finding the eigenvalues and eigenvectors of the upper triangular matrix T from Figure 3 of Schur’s Factorization (repeated in range R2:T4 of Figure 1 below).
Figure 1 – Eigenvectors of a non-symmetric matrix
Key formulas
The eigenvalues shown in range R8:T8 are the diagonal elements of T. The corresponding eigenvectors are shown in ranges R9:R11, S9:S11 and T9:T11 using the formulas shown in Figure 2.
| Cells/Range | Value/Formula |
| R2:T4 | =E32:G34 |
| R8:T8 | =DIAG(R2:T4) |
| R9, S10, T11 | 1 |
| R10, R11, S11 | 0 |
| S9 | =-1/(R2-S8)*S2 |
| T9:T10 | =-MMULT(MINVERSE(R2:S3-T8*Identity(2)),T2:T3) |
| T12 | =SQRT(SUMSQ(T9:T11)) |
| T27:T29 | =R9:T11/R12:T12 |
| V2:X4 | =A2:C4 |
| V8:X8 | = R8:T8 |
| V9:X11 | =MMULT(E27:G29,R9:T11) |
| V27:X29 | =V9:X11/V12:X12 |
Figure 2 – Formulas from Figure 1
The normalized versions of these eigenvalues are shown in R27:R29, S27:S29, and T27:T29. The eigenvalues of A (range V8:X8) are the same as those for T and the eigenvectors take the form QX (range V9:X11) where X are eigenvectors for T. Finally, unit eigenvectors of A are shown in range V27:X29.
Real Statistics Support
See Eigenvalue and Eigenvector Functions for how to obtain the eigenvalues and eigenvectors for any matrix, whether symmetric or non-symmetric, in Excel.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Golub, G. H., Van Loan, C. F. (1996) Matrix computations. 3rd ed. Johns Hopkins University Press
Searle, S. R. (1982) Matrix algebra useful for statistics. Wiley
Perry, W. L. (1988) Elementary linear algebra. McGraw-Hill
Fasshauer, G. (2015) Linear algebra.
https://math.iit.edu/~fass/532_handouts.html
Lambers, J. (2010) Numerical linear algebra
https://www.yumpu.com/en/document/view/41276350
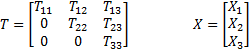
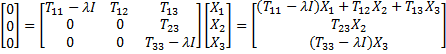
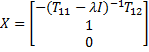
Charles,
I really appreciate your Real Statistics Excel add-in and information. I am an aeronautical engineer, working on a VERY complex analytical method, and my experience with eigen relations is very limited. I am ending up with a 4×4 unsymmetric matrix. The book that I am reading states this, “{a1 a2 b1 b2} are eigenvectors corresponding to two non-conjugate eigenvalues. In most cases, there will be four conjugate complex roots. However, only eigenvectors {a} and {b} corresponding to two nonconjugate eigenvalues will be utilized in the solution.”
I am really struggling with this solution. I am using your eVECT function and I am getting eigenvalues, eigenvectors, the MDETERM, and an [A][X]-L[X] values. How can I tell if the eigenvalues are real or imaginary? Will our add-in calculate the values that I need?
Hello Greg,
A symmetric real matrix can only have real eigenvalues. An asymmetric real matrix can have eigenvalues that are not real. All non-real complex eigenvalues occur in conjugate pairs (e.g. a+bi and a-bi).
The Real Statistics functions eVALUES and eVECT only return real eigenvalues. For example the 2 x 2 matrix
cos X -sin X
sin X cos X
has two non-real conjugate complex eigenvalues for most values of the angle X. If X = pi/4 then the array formula =eVALUES(A1:B2) returns the values
.707107 .707107
.5 .5
This means that if the eigenvalues were real, they would be .707107 (multiplicity 2), but the second row of the output are not zeros (they are instead .5). This means that the eigenvalues are not real and so you can ignore the values returned.
In fact, the correct eigenvalues are cos X + i sin X and cos X – i sin X, which for this example would be .707107 + .707107i and .707107 – .707107i. I am not sure whether eVALUES and eVECT always return the real part of the complex eigenvalues, but I wouldn’t count on it since I have investigated it.
Charles
Hi Charles Zaiontz
Thank you very much for the example.
I want to use Realstats to build Structural Decomposition Analysis model.
Please, any help (tutorial, example or template) would be appreciated.
Alnail,
Sorry, but Real Statistics doesn’t yet support structural decomposition analysis.
Charles