Divergence

Basic Concepts

Divergence is a measure of the difference between two probability distributions. Often this is used to determine the difference between a sample and a known probability distribution.

Divergence takes a non-negative value. The value is zero when the two probability distributions are equal.

We consider two measurements of divergence here.

Kullback-Leibler Divergence (KL)

Given two finite distributions p and q with corresponding elements x₁, …, x_n and y₁, …, y_n

We assume that when y_i = 0, then x_i = 0, and in this case, we set ln(x_i/y_i) = 0. Note too that it is assumed that the elements x₁, …, x_n and y₁, …, y_n are the values of a discrete probability distribution, and so each must sum to one. Thus, you may need to replace each x_i by x_i/, and similarly for the y_i.

We can also use the terminology KL(p||q) where p is the pdf whose values are x₁, …, x_n and q is the pdf whose values are y₁, …, y_n. We can view KL(p||q)  as representing the information gained by using p instead of q. From a Bayesian perspective, it measures the information gained when revising your prior beliefs from p to the posterior distribution q.

Note that KL(x||y) and KL(y||x) are not necessarily equal. The natural log can be replaced by a log of base 2.

Jensen-Shannon Divergence (JS)

Given two finite distributions p and q with corresponding elements x₁, …, x_n and y₁, …, y_n

where z_i = (x_i+y_i)/2. For this measure of divergence JS(x,y) = JS(y,x).

Examples

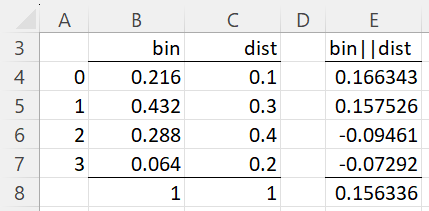
Example 1: Determine how well the discrete distribution displayed in column C of Figure 1 approximates the binomial distribution with n = 3 and p = .4.

Figure 1 – Kulback-Leibler divergence

The binomial distribution elements are shown in column B. E.g. cell B4 contains the formula =BINOM.DIST(A4,3,0.4,FALSE). We next insert the formula =B4*LN(B4/C4) in cell E4, highlight range E4:E7, and then press Ctrl-D. We calculate the Kulback-Leibler measure of divergence by placing the formula =SUM(E4:E7) in cell E8.

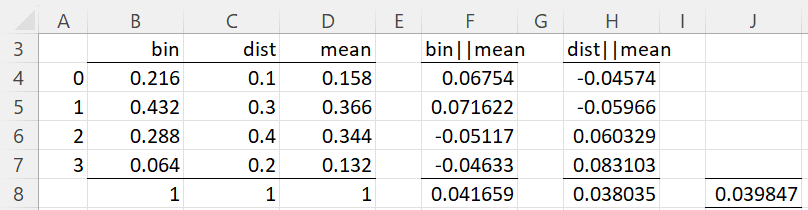
Example 2: Calculate the Jensen-Shannon divergence for the distributions from Example 1.

We first calculate the mean distribution as shown in column D of Figure 2. We then calculate KL(bin||mean) and KL(dist||mean) as shown in cells F8 and H8. Finally, JS(bin, dist) is the mean of these two values, namely .039847, as shown in cell J8.

Figure 2 – Jensen-Shannon divergence

Worksheet Functions

Real Statistics Functions: The Real Statistics Resource Pack provides the following worksheet functions where R1 and R2 are column arrays with the same number of rows.

KL_DIVERGE(R1, R2) = Kullback-Leibler divergence for R1 || R2

JS_DIVERGE(R1, R2) = Jenson-Shannon divergence for R1 and R2

E.g. the KL divergence measure for Example 1 can be calculated via the formula =KL_DIVERGE(B4:B7,C4:C7). Similarly, we can calculate the JD divergence measure for Example 2 via the formula =JS_DIVERGE(B4:B7,C4:C7).

Credit scoring divergence

There is also another measure of divergence which is used for credit scoring. Click here for more information about this type of divergence.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Wikipedia (2023) Divergence (statistics)
https://en.wikipedia.org/wiki/Divergence_(statistics)

Brownlee, J. (2019) How to calculate the KL divergence for machine learning. Machine Learning Mastery
https://machinelearningmastery.com/divergence-between-probability-distributions/

Wikipedia (2023) Kulback-Leibler divergence
https://en.wikipedia.org/wiki/Kullback%E2%80%93Leibler_divergence