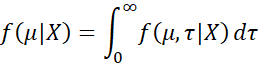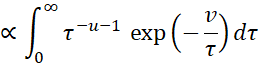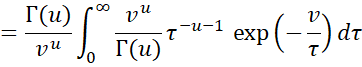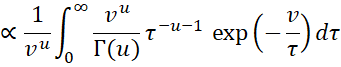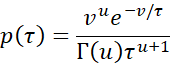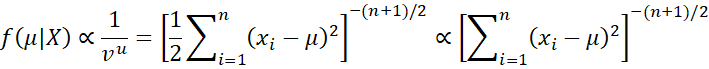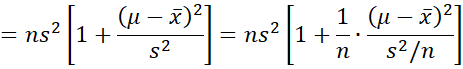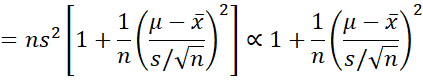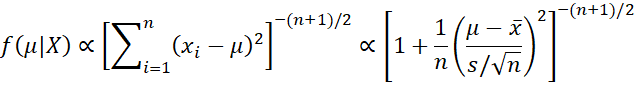Bayesian Hypothesis Testing Theory

Objective

We provide the theoretical basis for the results described in Bayesian Approach to Hypothesis Testing for normally distributed data.

One-sample test with unknown variance

Using the Jeffreys’ prior

f(μ, σ) = σ^-3

show that the posterior for μ is

where t_n is the non-standardized t-distribution. and s2 is the sample variance for the data set X using division by n instead of n-1.

Proof: Setting τ = σ², the joint posterior is

where

Thus, the posterior for μ is

Note that the pdf of the InvGamma(u, v) distribution (see Bayesian Distributions) is

which is the function inside the integral. Since this is a pdf, the integral is 1. Thus

Note that

Thus

where

This means that

Thus

References

Reich, B. J., Ghosh, S. K. (2019) Bayesian statistics methods. CRC Press

Lee, P. M. (2012) Bayesian statistics an introduction. 4^th Ed. Wiley
https://www.wiley.com/en-us/Bayesian+Statistics%3A+An+Introduction%2C+4th+Edition-p-9781118332573

Jordan, M. (2010) Bayesian modeling and inference. Lecture 1. Course notes
https://people.eecs.berkeley.edu/~jordan/courses/260-spring10/lectures/lecture1.pdf

Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., Rubin, D. B. (2014) Bayesian data analysis, 3^rd Ed. CRC Press
https://statisticalsupportandresearch.files.wordpress.com/2017/11/bayesian_data_analysis.pdf

Clyde, M. et al. (2022) An introduction to Bayesian thinking
https://statswithr.github.io/book/_main.pdf