Objective
In Statistical Power and Sample Size we show how to estimate the power of a statistical test and the related problem of determining the minimum sample size for a test to achieve a desired power. There we restricted ourselves to a one-tailed, one-sample z-test. We now address the two-tailed, one-sample z-test case.
Example 1: Repeat Example 2 of Statistical Power and Sample Size (parts a, b, and c) for a two-tailed test.
Determining Power
a) First we observe that the formula for the power of a two-tailed test is:
Here, n is the sample size, d is Cohen’s effect size, Φ(z) is the cdf of the standard normal distribution at z, and zcrit is the two-tailed critical value, namely NORM.S.INV(1 – α/2).
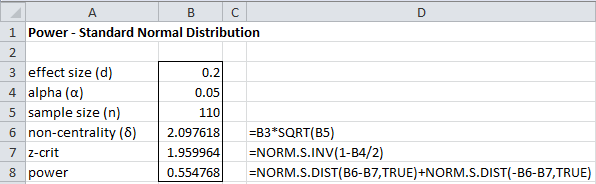
The power of this test is therefore 55.5%, as shown in Figure 1.
Figure 1 – Determining power for a two-tailed test
Determining Effect Size
b) Once again, we can calculate the effect size for a two-tailed z-test with power of 80% via the formula
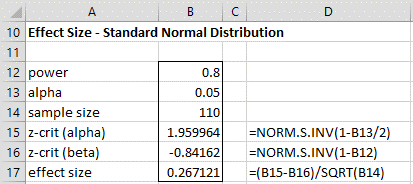
Using this formula, we see that the effect size is .267, as shown in Figure 2.
Figure 2 – Determining detectable effect size for a two-tailed test
Determining Sample Size
c) Once again, we can calculate the sample size for a two-tailed z-test with power of 80% via the formula
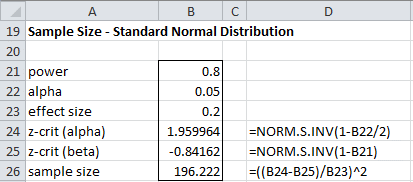
Using this formula, we see that the minimum sample size is 197, as shown in Figure 3.
Figure 3 – Determining the sample size for a two-tailed test
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Faul, F., Erdfelder, E., Buchner, A., & Lang, A. G. (2009). Statistical power analyses using G*Power 3.1: Tests for correlation and regression analyses. Behavior Research Methods, 41, 1149-1160.
http://link.springer.com/article/10.3758/BRM.41.4.1149
STAT (2015) Power and sample size reference manual, release 13
http://www.stata.com/manuals13/pss.pdf