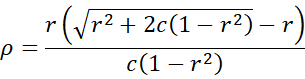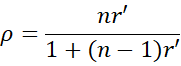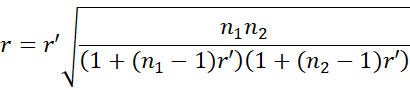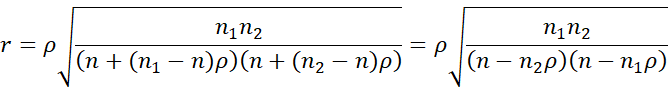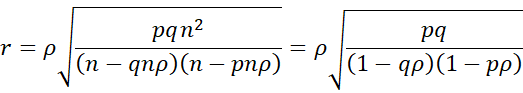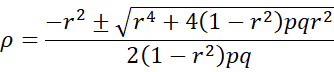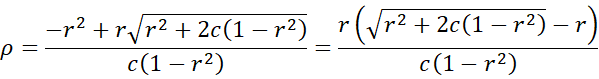Spearman-Brown Reliability Proof

Property 1: Where p = the proportion of the test due to the first half and c = 2p(1–p), the Spearman-Brown correction factor can be expressed as

Proof: We start with the following formula from Spearman-Brown’s Predicted Reliability.

Solving for r′ we get

But the reliability for the sum of n₁ units with the sum of the other n₂ units (where n = n₁ + n₂) is

Substituting the value for r′ in the above formula and simplifying, we get

Now let p = n₁/n and q = 1 – p = n₂/n. Thus, n1 = pn  and n2 = qn. Substituting these values in the above equation, we get

Squaring both sides of the resulting equation, we get

Using the quadratic formula, we get

Since ρ is expected to be non-negative, we use the positive square root. Finally, with c = 2pq, we have

References

Wikipedia (2016) Spearman-Brown prediction formula
https://en.wikipedia.org/wiki/Spearman%E2%80%93Brown_prediction_formula#:~:text=The%20Spearman%E2%80%93Brown%20prediction%20formula,after%20changing%20the%20test%20length.

Horst, P. (1951) Estimating total test reliability from parts of unequal length
https://onlinelibrary.wiley.com/doi/pdf/10.1002/j.2333-8504.1950.tb00474.x