Introduction
We illustrate some of the concepts from Markov Chains Basic Concepts via some examples in Excel.
Example 1
What is the probability that it will take at most 10 throws of a single die before all six outcomes occur?
Let S = {0,1,2,3,4,5,6} and xi = the number of different outcomes that have occurred by time i. Clearly, {x0, x1, ….} is an absorbing Markov chain where 6 is an absorbing state and x0 = 0. We start by observing that
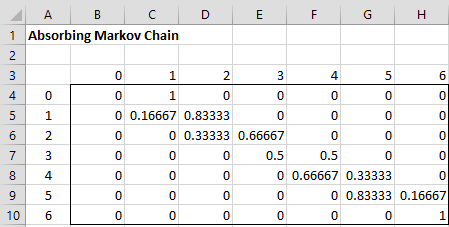
Using this information, we can represent the transition probability matrix P as shown in Figure 1.
Figure 1 – Transition Probability Matrix
Now, let z be a random variable that z or fewer throws of a single die before all six outcomes occur.
Since 6 is an absorbing state for any k, it follows that
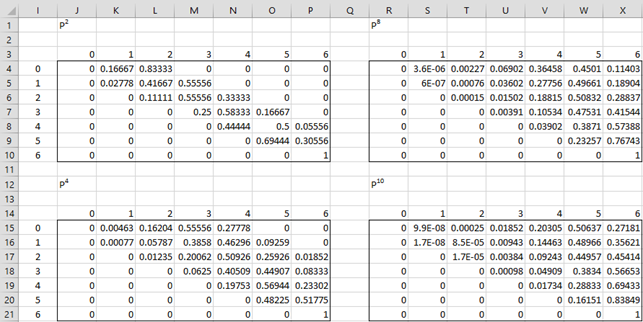
Thus, the probability that it will take at most 10 throws of a single die before all six outcomes occur is p1006. We need to calculate the 10-step transition probability matrix as shown in Figure 2.
Figure 2 – 10-step Transition Probability Matrix
P2 is calculated using the array formula =MMULT(B4:H10,B4:H10), P4 is calculated by the array formula =MMULT(J4:P10,J4:P10), P8 is calculated by =MMULT(J15:P21,J15:P21) and P10 is calculated by =MMULT(R4:X10,J4:P10).
Thus, the probability that it will take at most 10 throws of a single die before all six outcomes occur is p1006 = .27181 (cell X15).
Actually, the P10 matrix in range R15:X21 of Figure 2 can be calculated using the Real Statistics array formula =MPOWER(B4:H10,10). Note that we can calculate the value p906 = .1890 by using the formula =INDEX(MPOWER(B4:H10,10),1,7). Thus, the probability that it will take exactly 10 throws of a single die before all six outcomes occur is .27181 – .18904 = .08277.
Example 2
A die is repeatedly rolled. Bob wins a roll when 3, 4, 5 or 6 comes up and Jim wins a roll when 1 or 2 comes up. Bob wins the game if he wins 3 rolls in a row and Jim wins if he wins two rolls in a row. Determine the probability that Bob wins within 20 rolls. Determine the probability that Bob will win.
The first problem is similar to that of Example 1. The set of states S = {0, 1, 2, 3, a, b} where
0 = initial state
1 = Bob has won the last roll (but not the previous roll)
2 = Bob has won the last two rolls
3 = Bob has won three rolls in a row (absorbing state)
a = Jim has won the last roll
b = Jim has won two rolls in a row (absorbing state)
Thus
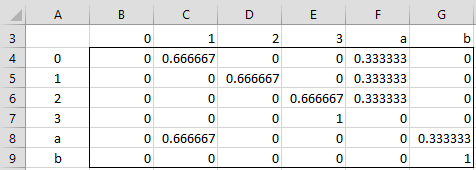
p01 = p12 = p23 = pa1 = 2/3
p0a = p1a = p2a = pab = 1/3
p33 = pbb = 1
and all other one-state transition probabilities are zero.
The one-state transition probability matrix is shown in Figure 3.
Figure 3 – Transition Probability Matrix
Result
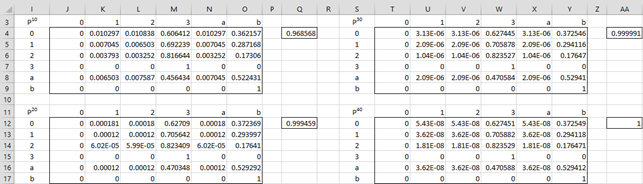
We now calculate P10, P20, P30 and P40 using the MPOWER function, as shown in Figure 4.
Figure 4 – Iteration to a Solution
From cell M20, we see that the probability that Bob wins within 20 rolls of the die is 60.64%. The probability that Jim wins within 20 rolls is 37.24% (cell O4). The probability that someone wins within 20 rolls is therefore 60.64% + 37.24% = 99.55% (cellQ4).
Note that as we increase the number of rolls, two things happen. First, the probability that someone wins approaches 100%. E.g. after 40 rolls, this probability has already reached 100% (cell AA12), at least to 5 decimal places. Second, successive values of Pk don’t change much (convergence), as can be seen by comparing P30 with P40.
From cell W12, we see that the probability that Bob wins is 62.75%. The probability that Jim wins is 37.25%.
Alternative Approach
We now show another way of calculating the probability that Bob wins. Let qs be the probability that Bob wins starting with state s. By the law of conditional probability it follows that
Thus
where q3 = 1 and qb = 0. We now solve these equations.
and so q1 = 12/17. Thus
It now follows that
which is the same answer we got previously.
Example 3
Find the expected number of rolls before someone wins the game described in Example 2.
Once again we need a set of simultaneous equations. Let μs be the expected number of rolls until someone wins starting with state s. By the law of conditional expectations, it follows that
Since
we conclude that
But note that p01 = p12 = p23 = pab = 2/3 and p0a = p1a = p2a = pab = 1/3. All other psr = 0. Hence
where μ3 = μa = 0. We now solve the four equations in four unknowns. Actually, without the first equation, we have three equations in three unknowns. We start with
which is equivalent to
which means that
and so
Finally, we see that
We now find the other expected values as follows
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Fewster, R. (2014) Markov chains
https://www.stat.auckland.ac.nz/~fewster/325/notes/ch8.pdf
Pishro-Nik, H. (2014) Discrete-time Markov chains
https://www.probabilitycourse.com/chapter11/11_2_1_introduction.php
Norris, J. (2004) Discrete-time Markov chains
https://www.statslab.cam.ac.uk/~james/Markov/
Lalley, S. (2016) Markov chains
https://galton.uchicago.edu/~lalley/Courses/312/MarkovChains.pdf
Konstantopoulos, T. (2009) Markov chains and random walks
https://www2.math.uu.se/~takis/L/McRw/mcrw.pdf
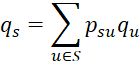
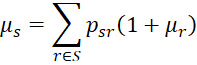
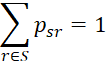
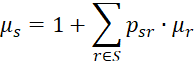
Dear Charles,
the multiplication of two matrices (p*p) in your example (figure 1) by MMULT function gives me the result of zero matrix, however in your example it is not zero matrix. I tried and multiplied different two matrices and got a result and this means that MMULT function generally works. tell me please what can be a problem in this case?
Hi Sandro,
Can you email me a spreadsheet showing that the multiplication p x p is a zero matrix?
Charles