Objective
On this webpage, we extend the approach described for Multivariate One Between-subjects and One Within-subjects Factor to the case where there is one between-subjects factor and two within-subjects factors. This is accomplished by combining the approach described on that webpage with the approach described in Two Multivariate Within-subjects Factors.
We illustrate this by repeating Example 1 of Repeated Measures ANOVA with One Between-subjects and Two Within-subjects Factors.
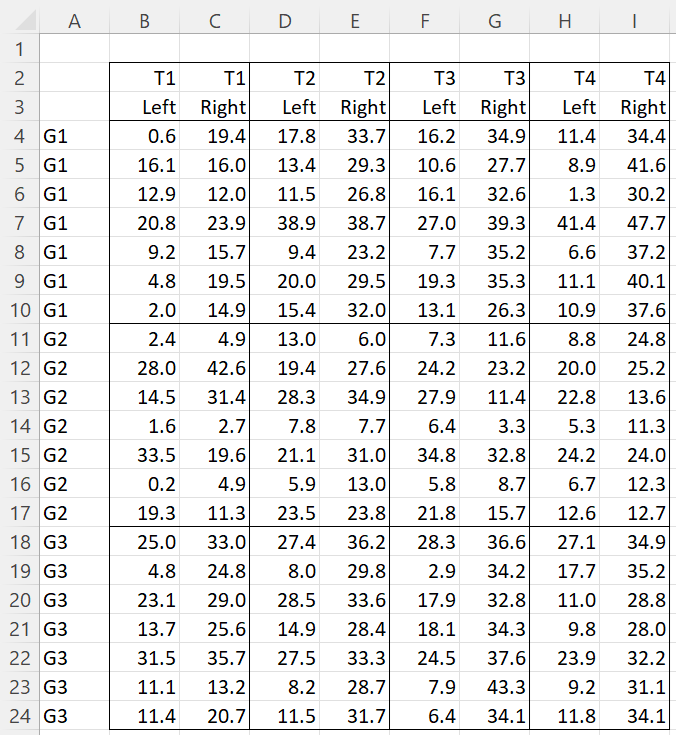
Example 1: Suppose there are three groups (G1, G2, G3), and each subject in these three groups was given 4 types of dexterity tests (T1, T2, T3, T4), each repeated once using the left hand and the other using the right hand. All the subjects in the experiment were right-handed. The data for this example are as shown in Figure 1.
Figure 1 – Data for Repeated Measures ANOVA 2W+1B
This time we will use a MANOVA approach. Note that for the Repeated Measures ANOVA, we specified that the between-subjects factor was balanced with three levels, and so we only needed to supply a label for cells A4, A11, and A18. When using the MANOVA approach (which requires that the data be in standard format), labels must be supplied for all the entries in range A4:A24.
Data Analysis Tool
Real Statistics Data Analysis Tool: The Repeated Measures Manova (2W+1B) data analysis tool can be used to perform the repeated measures analysis with one between-subjects factor and two within-subjects factors using a MANOVA approach.
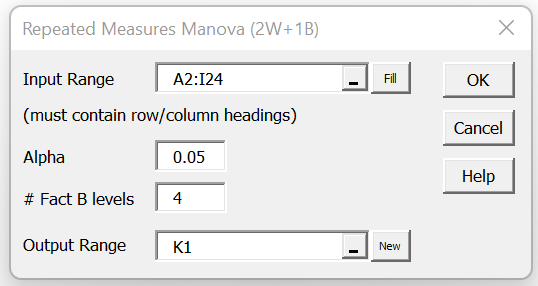
For Example 1, press Ctrl-m and choose the Repeated Measures Manova (2W+1B) option from the MultiVar tab (or from the Manova option if using the original user interface). Now fill in the fields in the dialog box that appears as shown in Figure 2 and click on the OK button.
Figure 2 – Dialog Box
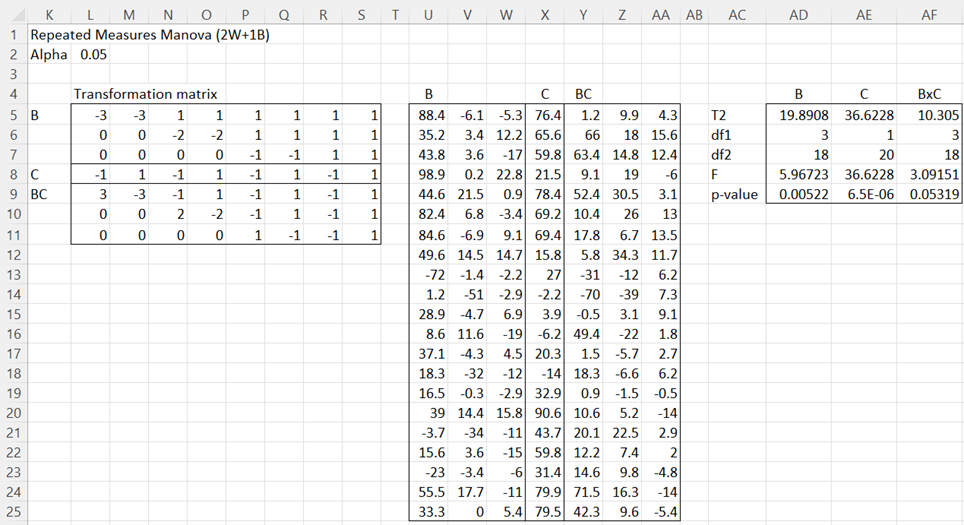
Output for B, C, and B × C Factors
The output begins with the results for the B, C, and B × C factors, that is the within-subjects factors. This is identical to the analysis obtained by using the Repeated Measures Manova (2W+0B) data analysis tool on the data in B4:I24. This is shown in Figure 3.
Figure 3 – B, C and B × C analyses
This result doesn’t take the between-subject factor into account.
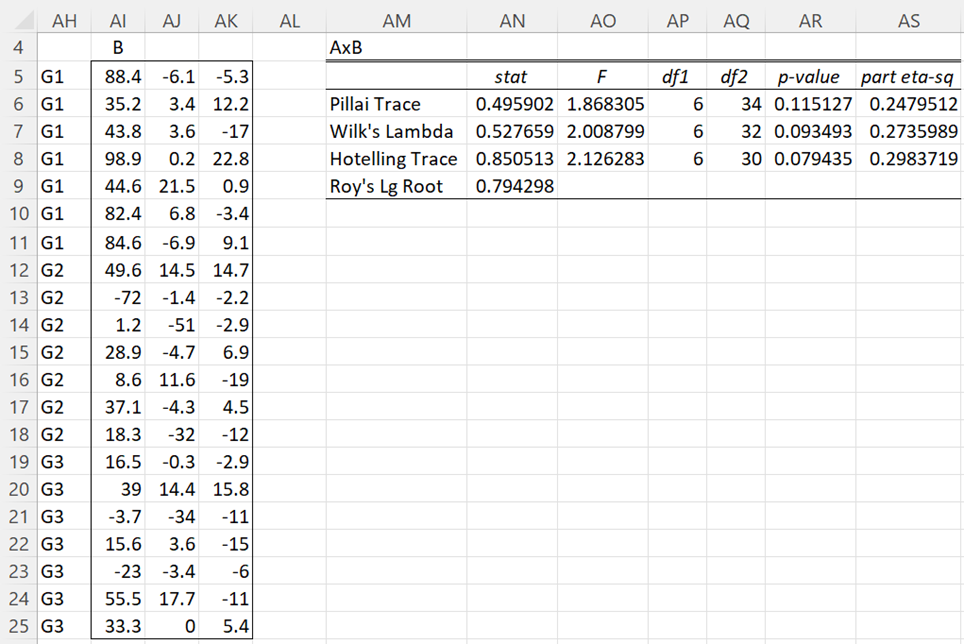
Output for A × B, A × C, and A × B × C Factors
The next part of the output provides the results for the A × B factor.
Figure 4 – A × B analysis
The output uses the data from range A4:A24 and U5:W25, repeated in range AH5:AK25, and performs a one-factor MANOVA to obtain the results shown on the right side of Figure 4.
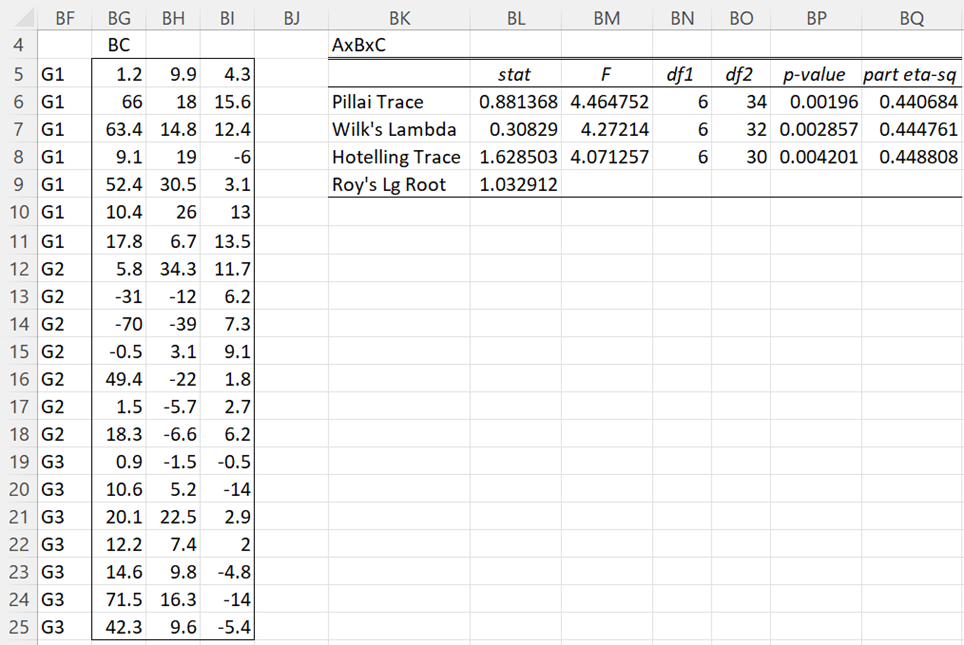
The analyses for A × B and A × B × C are similar. The analysis for A × B uses the data from range A4:A24 combined with that from X5:X25. The analysis for A × B × C uses the data from range A4:A24 combined with that from Y5:AA25. The results are shown in Figures 5 and 6.
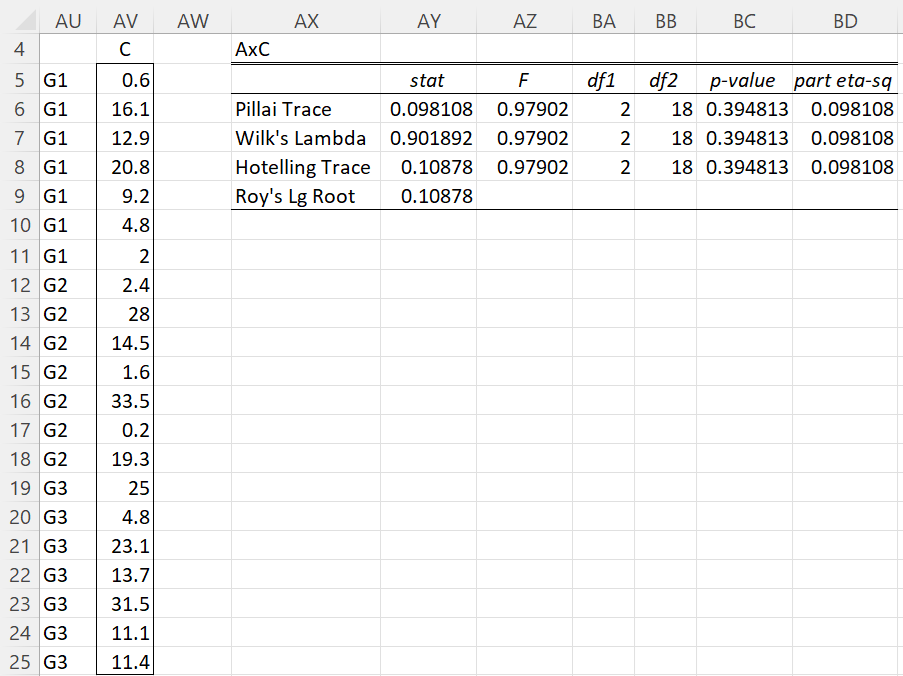
Figure 5 – A × C analysis
Since A × B only has one dependent variable, the results obtained using MANOVA are identical to those obtained by using one-way ANOVA. In particular, the df1, df2, F, p-value, and partial eta-square values will be the same.
Figure 6 – A × B × C analysis
Output for A
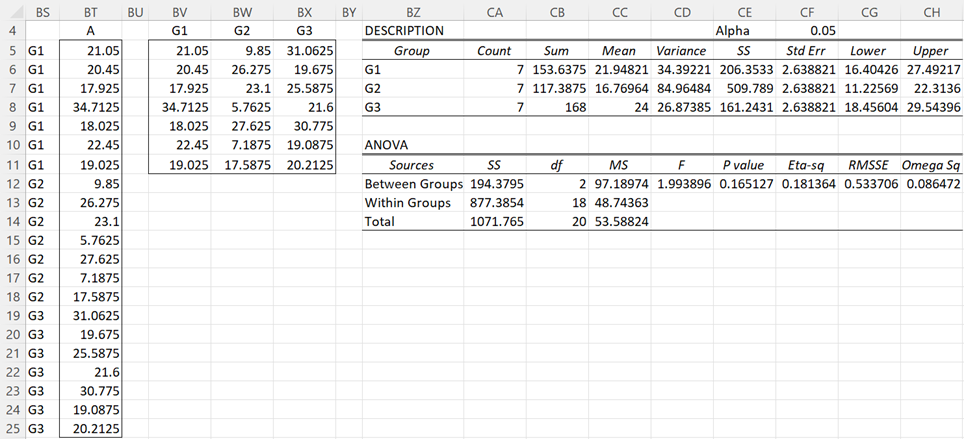
The output from the data analysis tool concludes with the analysis of Factor A. Here a one-way ANOVA is performed as shown in Figure 7. The values in range BT5:BT25 are obtained by using the array formula =MEANROW(B4:I24) and the values in range BV4:BX11 are obtained by using the array formula =StdAnova1(BS5:BT25).
Figure 7 – Factor A analysis
Observation
Finally, note that additional information can be obtained by using the One Factor MANOVA and One Factor ANOVA data analysis tools. This includes follow-up analyses. The appropriate data sets, as shown in the above figures, are used.
References
Rencher, A.C. (2002) Methods of multivariate analysis (2nd Ed). Wiley-Interscience, New York.
https://www.ipen.br/biblioteca/slr/cel/0241