Objective
Our objective is to show how to use bootstrapping in PLS regression modelling. In particular, we describe how to estimate standard errors and confidence intervals for regression coefficients, and prediction intervals for modeled data.
We follow the approach described in Multivariate Regression Bootstrapping, and so on this webpage we describe the Excel worksheet functions provided by the Real Statistics Resource Pack.
Worksheet Functions
The following functions support bootstrapping for a regression model with intercept using Approach 2 based on Rx and Ry where Rx is an n × k array of X data, Ry is an n × m array of Y data. iter (default 2000) bootstrap samples are generated. alpha is the significance level (default .05).
Resampling cases
PLSRegCovBoot(Rx, Ry, iter): returns the covariance matrix of the regression coefficients
PLSRegCIBoot(Rx, Ry, iter, alpha): returns an array with km+1 rows, one per regression coefficient. Each row contains the mean value of the regression coefficient, the standard error, and the lower and upper ends of the 1-alpha confidence interval
PLSRegPredBoot(Rx0, Rx, Ry, iter, alpha, pred): returns an array with rm rows where Rx0 is a k × r array. Each row in Rx0 specifies X values. Each row in the output consists of the predicted value for the data in the corresponding row of Rx0 based on the regression of Ry on Rx, its standard error, and the lower and upper ends of the 1-alpha prediction/confidence interval. If pred = TRUE (default), then the prediction interval is output: otherwise, the confidence interval is output.
Resampling residuals
The following worksheet functions are similar to the above functions except that bootstrap based on resampling residuals is employed.
PLSRegCovBootRes(Rx, Ry, iter): returns the covariance matrix of the regression coefficients
PLSRegCIBootRes(Rx, Ry, iter, alpha): returns the regression coefficients, the standard errors, and the 1-alpha confidence intervals
PLSRegPredBootRes(Rx0, Rx, Ry, iter, alpha, pred): returns the predictions, s.e., and 1-alpha prediction/confidence intervals
Examples
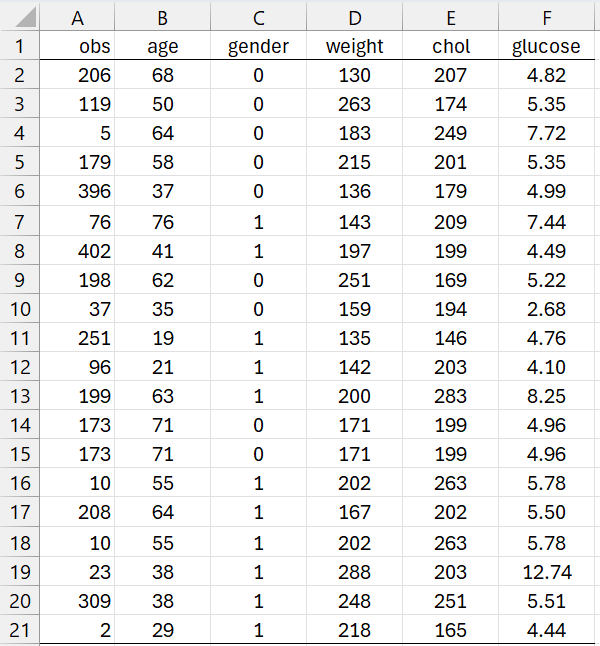
For the following examples, we use the cholesterol and glucose data in Figure 1.
Figure 1 – Cholesterol/glucose level data
Coefficients
We first calculate the regression coefficients based on 1, 2, and 3 latent vectors, as shown in Figure 2. E.g. range H1:J5 contains the formula
=PLSRegCoeff(B1:D21,E1:F21,1,TRUE)
Figure 2 – PLS regression coefficients
We will use the one latent vector model and bootstrapping by resampling cases for the remaining examples.
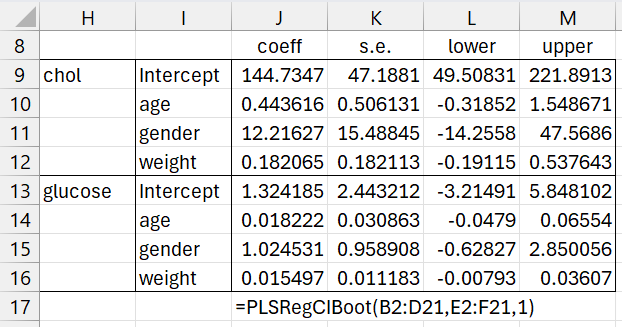
We next use bootstrapping to estimate the standard errors and 95% confidence intervals for each of the regression coefficients, as shown in Figure 3. Here, the headings have all been added manually to the output of the displayed formula in range J9:M16.
Figure 3 – Coefficient confidence intervals
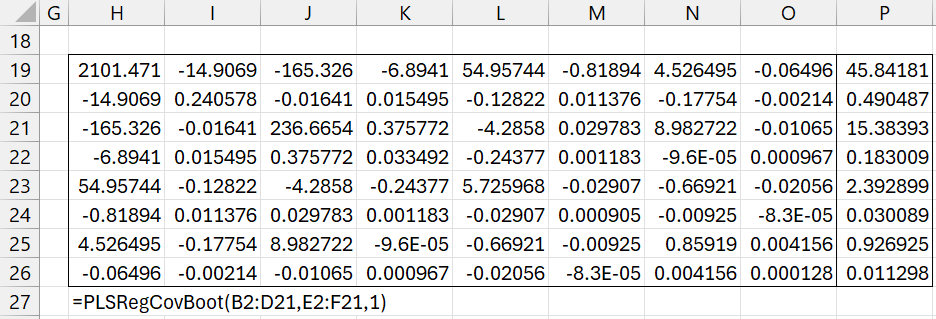
We next estimate the coefficient covariance matrix in Figure 4 using bootstrapping by resampling cases. By placing the array formula =SQRT(DIAG(H19:O26)) in range P19:P26, we obtain the standard errors, which we can compare with those in column K of Figure 2.
Figure 4 – Coefficient covariance matrix
Predictions
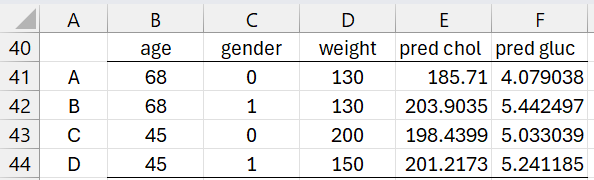
Using the PLS regression described in range H1:J5 of Figure 2, we can predict the cholesterol and glucose levels for each of the four scenarios described in Figure 5.
Figure 5 – Scenarios
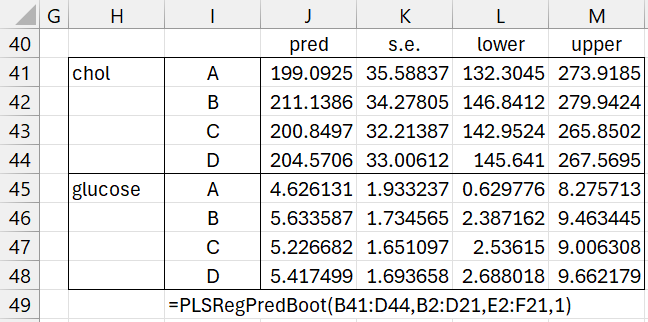
We now use bootstrapping to estimate standard errors and 95% prediction intervals for these predictions. These are shown in Figure 6.
Figure 6 – Bootstrapping prediction intervals
We can also use the resampling residuals to obtain prediction and confidence intervals.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Eck, D. J. (2017) Bootstrapping for multivariate linear regression models
https://arxiv.org/abs/1704.07040
Stine, R. A. (1985) Bootstrap prediction intervals for regression
https://www.jstor.org/stable/2288570?seq=1
Fox, J. (2015) Bootstrapping regression models.
Applied Regression Analysis and Generalized Linear Models, 3rd ed. Sage Publishing
https://us.sagepub.com/sites/default/files/upm-binaries/21122_Chapter_21.pdf
Stack Exchange (2021) Bootstrap prediction interval
https://stats.stackexchange.com/questions/226565/bootstrap-prediction-interval
Roustant, O. (2017) Bootstrap & confidence/prediction intervals
https://olivier-roustant.fr/wp-content/uploads/2018/09/bootstrap_conf_and_pred_intervals.pdf