Overview
We now explore the confidence interval of multivariate regression coefficients. We also show how to calculate them in Excel. Note that these intervals don’t take into account the multivariate nature of the regression. To gain more insight into this subject, see Multivariate Regression Hypothesis Testing.
Simultaneous confidence intervals
Based on the normality assumption
a simultaneous 1-alpha confidence interval for the pth column of the multivariate regression coefficient matrix βp is
where
MSRes = SSRes/dfRes dfRes = n – k – 1
Individual confidence intervals
Usually, however, we use the individual confidence intervals of the βjp instead of the simultaneous confidence intervals. These are defined as in the univariate case by
where
Example
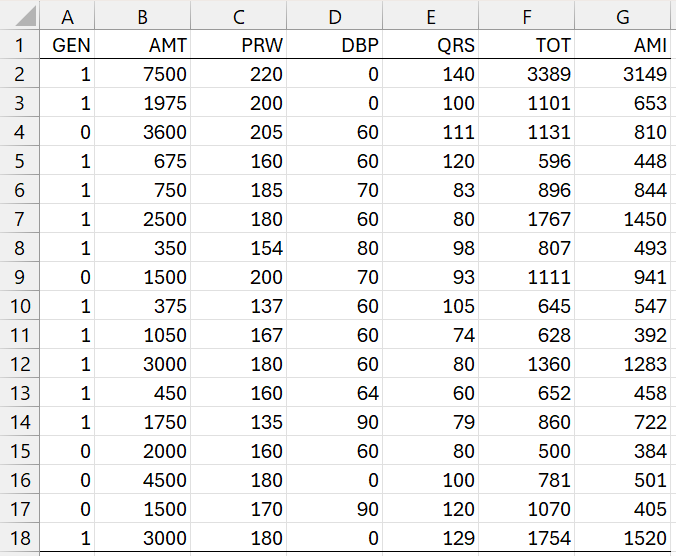
Example 1: Find the 95% confidence intervals for the multivariate regression coefficients based on the data in Figure 1.
Figure 1 – Amitriptyline Data
This data is taken from Johnson and Wichern (2007). The first five columns contain data for the 5 independent variables and the last two contain data for the 2 dependent variables.
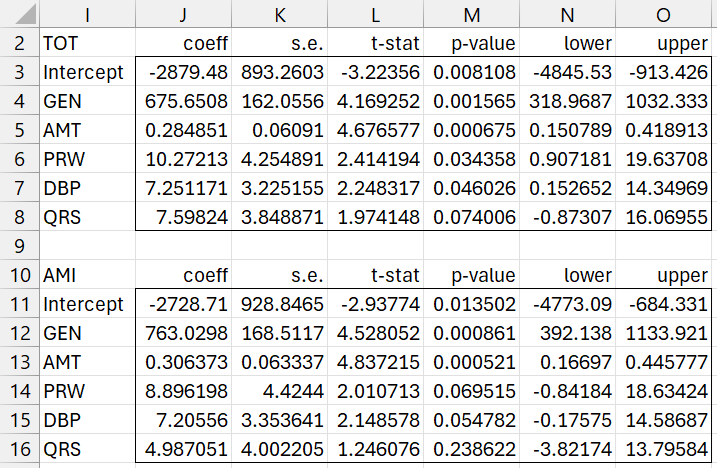
Figure 2 displays the results. These results are the same as for two separate multiple regression models, one for each dependent variable.
Figure 2 – Confidence intervals for regression coefficients
Here, range I2:O8 contains the array formula =RegCoeffCI(A1:E18,F1:F18,TRUE) and range I10:O16 contains the formula =RegCoeffCI(A1:E18,G1:G18,TRUE).
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Johnson, R. A., Wichern, D. W. (2007) Applied multivariate statistical analysis. 6th Ed. Pearson
https://mathematics.foi.hr/Applied%20Multivariate%20Statistical%20Analysis%20by%20Johnson%20and%20Wichern.pdf
Helwig, N. E. (2017) Multivariate linear regression
http://users.stat.umn.edu/~helwig/notes/mvlr-Notes.pdf
Ford, C. (2023) Getting started with multivariate multiple regression
https://library.virginia.edu/data/articles/getting-started-with-multivariate-multiple-regression#:~:text=Multivariate%20Multiple%20Regression%20is%20a,parent%20income%2C%20and%20so%20forth.