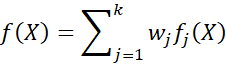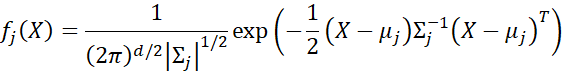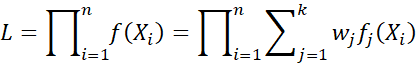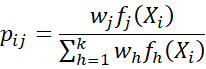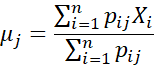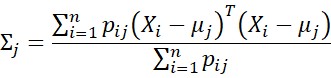Multivariate GMM

Introduction

As described in Univariate GMM, Gaussian Mixture Models (GMM) are  models that represent normally distributed subpopulations where each subpopulation may have different parameters and for each element in the population we don’t know a priori which subpopulation that data element belongs to. We assume that the subpopulations have the same dimension.

For multivariate GMM models, we are dealing with subpopulations (aka components) that follow a multivariate normal distribution, and so the parameters are the mean vector and covariance matrix of each component.

Objective

On this webpage we describe how to create a GMM model based on mutivariate data. We start with a sample of size n and assume that there are k subpopulations C1, …, Ck. Our objective is to estimate the parameters of the multivariate normal distribution for each of the k subpopulations. More specifically, for each i, we want to estimate the mean vector μi and covariance matrix Σi so that for a data vector X in Ci, X ∼ N(μi, Σi). 

We also want to determine for any X (in the sample or population) what is the probability that X belongs to subpopulation Ci for i = 1, 2, …, k. We can, if we choose, then assign X to that subpopulation with the highest probability. This is a form of cluster analysis where the Ci are the clusters. This is a type of “soft clustering” since the assignment probabilities are produced, unlike k-means clustering where only an assignment cluster is made.

Model Specification

The GMM model is specified by the following parameters:

  • k = number of components
  • wj = weight (aka the mixture coefficient) of the jth component where the sum of the weights is 1
  • μj = mean vector of the jth component
  • Σj = covariance matrix of the jth component

For each X in the population, the pdf f(X) at X is

Multivariate normal mixture pdf

where fj(X) is the probability density function (pdf) of a d-dimensional multivariate normal distribution with mean vector μj and covariance matrix Σj, i.e.

Multivariate normal pdf

Excel doesn’t provide a multivariate normal distribution worksheet function, and so we use the following Real Statistics worksheet function:

fj(X) = MNORMDIST(X, μj, Σj, FALSE)

The model parameters are estimated from a sample X1, X2, …, Xn as explained next.

Model Estimation

We estimate the model parameters μj, Σj, and wj by maximizing the log-likelihood function

Likelihood function L

or equivalently, the log-likelihood function

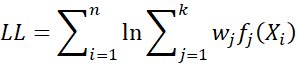
Log-likelihood function LL

This is done using the Expectation-Maximization (EM) algorithm (see EM Algorithm). This is a type of unsupervised learning, and consists of the following steps.

Step 0 (initialization)

  • Estimate wj by 1/k for each component.
  • Select k elements randomly without replacement from the sample and assign these as estimates for μ1, …, μk.
  • Estimate Σj for all j by the sample covariance matrix

There are a number of alternative approaches for initializing the μj, Σj, and wj parameters, including using the results from k-means clustering.

Step m for m > 0 (EM algorithm)

We now perform a series of EM steps consisting of an E step followed by an M step. 

E step

For each i = 1, …, n and j = 1, …, k, define pij = the probability that sample element Xi is in component Cj, namely

p_ij

where fh(x) is the pdf of the multivariate normal distribution with the current estimates of μh and Σh.

M step

Re-estimate the model parameters as follows:

w_j

mu_j

Covariance matrix j

Termination

We repeat the EM steps until a maximum number of iterations is reached or until some sort of convergence criterion is met.

Observations

For clustering, GMM has the following advantages over K-means clustering:

  • The centroids for K-means clustering are circles (or hyper-spheres), while GMM uses ellipses (or hyper-ellipses), which provides a better fit.
  • K-means clustering assigns data elements to one cluster (hard clustering), while GMM assigns data elements to a mixture of clusters, each with a probability (soft clustering).

References

McGonagle, J. et al (2024) Gaussian mixture model
https://brilliant.org/wiki/gaussian-mixture-model/

Carrasco, O. C. and Whitfield, B. (2024) Gaussian mixture models explained
https://builtin.com/articles/gaussian-mixture-model

GeeksforGeeks (2023) Gaussian mixture model
https://www.geeksforgeeks.org/gaussian-mixture-model/

Apgar, V. (2023) 3 use-cases for Gaussian Mixture Models (GMM)
https://towardsdatascience.com/3-use-cases-for-gaussian-mixture-model-gmm-72951fcf8363

Leave a Comment