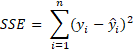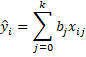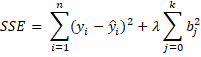Introduction
Ordinary least squares (OLS) regression produces regression coefficients that are unbiased estimators of the corresponding population coefficients with the least variance. This is the Gauss-Markov Theorem. In most situations, this is exactly what we want. If a large number of samples are taken and we calculate the OLS coefficients for each sample, then the average value of each of these coefficients will be pretty close to the population value of this coefficient, and there will be minimal variation from one sample to the next (i.e. variances will be as small as possible).
When OLS is not the best
However, there may be a model with less variance (i.e. smaller SSE), but at the cost of added bias. This may be desirable, for example, when some of the data is highly correlated. This occurs in the following situations:
- There are many independent variables, especially when there are more variables than observations.
- Data is close to multicollinearity, in which case XTX is not invertible or is close to being non-invertible, which means that small changes to X can result in large changes to (XTX)-1 and therefore to the values of the regression coefficients.
Here the OLS model over-fits the data, i.e. it captures the data well but is not so good at forecasting based on new data. In these cases, Ridge and LASSO Regression can produce better models by reducing the variance at the expense of adding bias.
Ridge Regression
In ordinary linear (OLS) regression, the goal is to minimize the sum of squared residuals SSE.
For Ridge regression, we add a factor as follows:
where λ is a tuning parameter that determines how much to penalize the OLS sum of squares. If λ = 0, then we have the OLS model, but as λ → ∞, all the regression coefficients bj → 0.
The OLS regression coefficients (and therefore of SSE) produces unbiased estimators of the population values. The Ridge regression value of SSE adds bias, but with the benefit that it reduces the variance. The smaller the value of λ, the less the bias, but the larger the value of λ, the lower the variance.
The variance is reduced because in those situations in which Ridge regression is applicable, the values of the OLS regression coefficients tend to be large. The purpose of the extra term in the formula for SSE is to reduce the size of the regression coefficients. The larger the value of lambda the smaller the size of the coefficients, but the more bias. The goal is to find a value that optimizes the tradeoff between bias and variance.
Properties
In the OLS case, we found that (Property 1 of Multiple Regression using Matrices) the coefficient vector can be expressed as:
The covariance matrix of the coefficients can be expressed as
We have a similar result for Ridge regression, namely
Property 1:![]()
Here the λI term is considered to be the ridge (i.e. values added to the main diagonal of XTX).
Observations
In order to penalize all the estimated coefficients equally, it is best to standardize all the x data values prior to using Ridge regression. We also standardize the y data values. In Excel, this can be done by using the STANDARDIZE or STDCOL function. Also, since we have standardized all the data, an intercept term is not used.
The variance inflation factor (VIF) for the Ridge regression coefficients is given by
where λ* = λ/(n–1) and R is the correlation matrix of X data (standardized or not), i.e.
![]()
References
bquanttrading (2015) Ridge regression in Excel/VBA
https://asmquantmacro.com/2015/12/11/ridge-regression-in-excelvba/
Marquardt, D. W. and Snee, R. D. (1975) Ridge regression in practice. The American Statistician
https://web.archive.org/web/20170809092848/http://www.jarad.me/stat615/papers/Ridge_Regression_in_Practice.pdf
PennState (2018) Ridge regression. Applied Data Mining and Statistical Learning
https://online.stat.psu.edu/stat857/node/155/