Objective
The Real Statistics Resource Pack provides a number of worksheet functions to support bootstrapping for regression in Excel. We describe these functions and give some examples of their use.
Worksheet Functions
The following functions support bootstrapping for a regression model with intercept using Approach 2 based on Rx and Ry where Rx is an n × k array of X data, Ry is an n × 1 array of Y data. iter (default 2000) bootstrap samples are generated. alpha is the significance level (default .05).
Resampling Cases
RegCovBoot(Rx, Ry, iter, dprec): returns the covariance matrix of the regression coefficients
RegCIBoot(Rx, Ry, iter, alpha, dprec): returns an array with k+1 rows, one per regression coefficient. Each row contains the mean value of the regression coefficient, the standard error, and the lower and upper ends of the 1-alpha confidence interval
RegPredBoot(Rx0, Rx, Ry, iter, alpha, dprec, pred): returns an array with r rows where Rx0 is a k × r array. Each row in Rx0 specifies X values. Each row in the output consists of the predicted value for the data in the corresponding row of Rx0 based on the regression of Ry on Rx, its standard error, and the lower and upper ends of the 1-alpha prediction/confidence interval. If pred = TRUE (default), then the prediction interval is output: otherwise, the confidence interval is output.
When creating a bootstrap sample using resampling cases, if ZTZ is not invertible for one of the samples Z, then we don’t want to include this sample. In fact, if Abs(det ZTZ) < dprec then this sample is excluded. This is generally an issue only when the original sample is small, and so selecting rows with replacement can lead to too many duplicates.
Resampling residuals
The following worksheet functions are similar to the above functions except that bootstrap based on resampling residuals is employed. Note that the dprec argument is not needed.
RegCovBootRes(Rx, Ry, iter): returns the covariance matrix of the regression coefficients
RegCIBootRes(Rx, Ry, iter, alpha): returns the regression coefficients, the standard errors, and the 1-alpha confidence intervals
RegPredBootRes(Rx0, Rx, Ry, iter, alpha, pred): returns the predictions, s.e., and 1-alpha prediction/confidence intervals
Examples
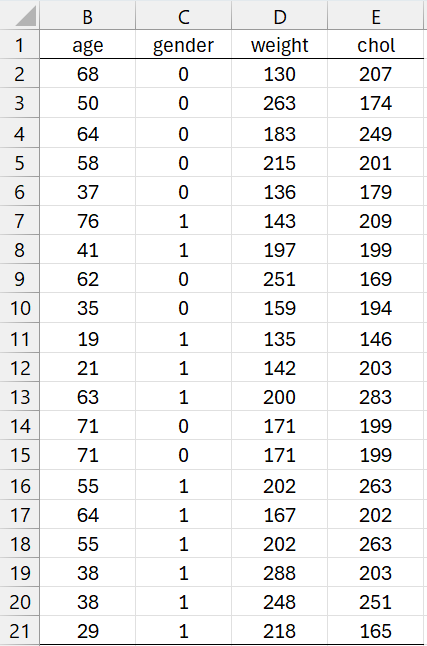
For the following examples, we use the cholesterol data in Figure 1.
Figure 1 – Cholesterol data
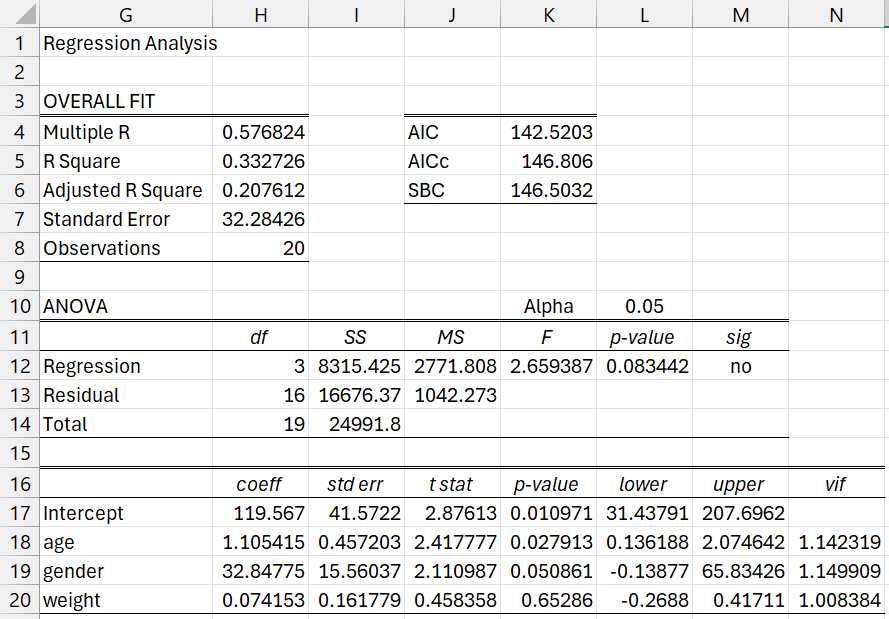
We now use Real Statistics’ Regression Analysis data analysis tool with the results shown in Figure 2.
Figure 2 – Regression Analysis
Coefficients
We next use bootstrapping to estimate the standard errors and confidence intervals for each of the regression coefficients, as shown in Figure 3. We do this by placing the formula =RegCIBoot(B2:D21,E2:E21) in range H23:J26 and =RegCIBootRes(B2:D21,E2:E21) in range H29:J32. Note that the results are fairly similar to the normal approximations shown in Figure 2.
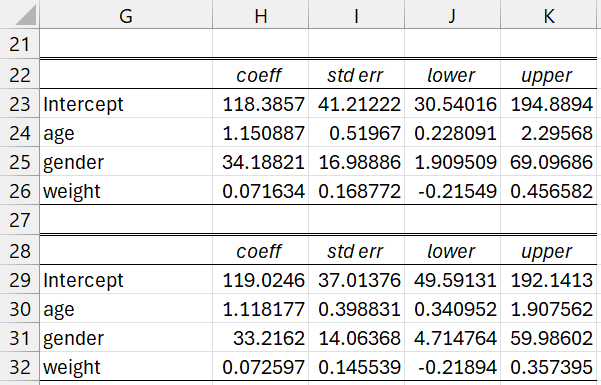
Figure 3 – Bootstrap coefficient confidence intervals
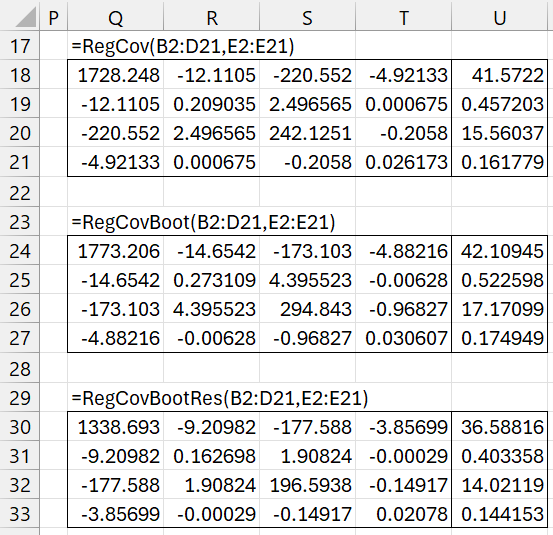
We next show three estimates of the coefficient covariance matrix in Figure 4. The first estimate is based on the normal assumption, while the other two use bootstrapping.
Figure 4 – Bootstrap coefficient covariance matrix
Range U18:U21 contains the formula =SQRT(DIAG(Q18:T21)), which shows the standard errors for the coefficients. The bootstrap estimates for the standard errors are shown in ranges U24:U27 and U30:U33. You can compare these with the results shown in Figure 3.
Predictions
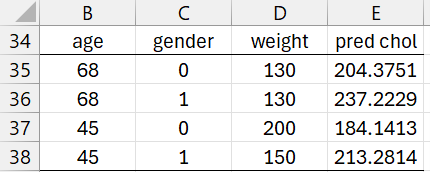
We now explore the four scenarios described in range B34:D38 of Figure 5. Using the regression described in Figure 2, we can predict the cholesterol levels for each scenario. These are shown in range E35:E38 using the formula =RegPredC(B35:D38,H17:H20).
Figure 5 – Scenarios
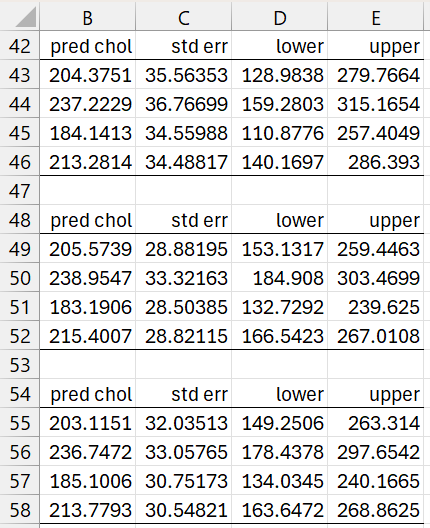
We now show three ways of estimating the confidence intervals for these four scenarios (see Figure 6).
Figure 6 – Confidence intervals
The first uses the formula =RegPredPI(B35:D38,B2:D21,E2:E21,,FALSE) based on the normality assumption. The other two use bootstrapping as calculated by the formulas
=RegPredBoot(B35:D38,B2:D21,E2:E21,,,,FALSE) =RegPredBootRes(B35:D38,B2:D21,E2:E21,,,FALSE)
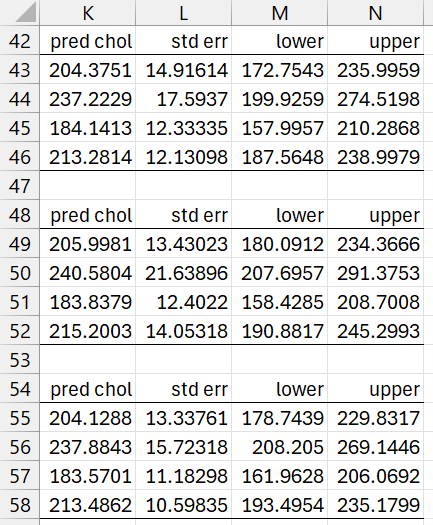
Figure 7 shows three ways of estimating the prediction intervals for these four scenarios.
Figure 7 – Prediction intervals
These use the formulas
=RegPredPI(B35:D38,B2:D21,E2:E21)
=RegPredBoot(B35:D38,B2:D21,E2:E21) =RegPredBootRes(B35:D38,B2:D21,E2:E21)
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Eck, D. J. (2017) Bootstrapping for multivariate linear regression models
https://arxiv.org/abs/1704.07040
Stine, R. A. (1985) Bootstrap prediction intervals for regression
https://www.jstor.org/stable/2288570?seq=1
Fox, J. (2015) Bootstrapping regression models.
Applied Regression Analysis and Generalized Linear Models, 3rd ed. Sage Publishing
https://us.sagepub.com/sites/default/files/upm-binaries/21122_Chapter_21.pdf
Stack Exchange (2021) Bootstrap prediction interval
https://stats.stackexchange.com/questions/226565/bootstrap-prediction-interval
Roustant, O. (2017) Bootstrap & confidence/prediction intervals
https://olivier-roustant.fr/wp-content/uploads/2018/09/bootstrap_conf_and_pred_intervals.pdf
Kumar, A. (2020) Bootstrapping to re-estimate parameters in small samples
No longer available online
Turgeon, M. (2021) Bootstrap and linear regression
https://www.maxturgeon.ca/f21-stat3150/slides/bootstrap-linreg.pdf