Singular Value Decomposition

Basic Concepts

Property 1 (Singular Value Decomposition): For any m × n matrix A there exists an m × m orthogonal matrix U, an n × n orthogonal matrix V and an m × n diagonal matrix D with non-negative values on the diagonal such that A = UDVT.

In fact, such matrices can be constructed where the columns of U are the eigenvectors of AAT, the columns of V are the eigenvectors of ATA and the main diagonal of D contains the square roots of the eigenvalues of U (or V) in descending order.

Proof: By Property 2 of Positive Definite Matrices, ATA is a positive semidefinite n × n matrix, and so by Property 1 of Positive Definite Matrices, it is symmetric. By Theorem 1 of Spectral Decomposition, it has a spectral decomposition ATA = VEVT where V is an orthogonal n × n matrix whose columns are unit eigenvalues of ATA and E is an n × n diagonal matrix whose main diagonal consists of the eigenvalues λ1, …, λn of ATA in descending order. Since ATA is positive semidefinite, these eigenvalues are non -negative. Thus there is an r such λ1 ≥ … ≥ λr >0 and λr+1 =⋯= λn = 0.

Since Vj is a unit vector

image9358

and so AVj = 0 when j > r. We now construct an m × m matrix U as follows. First define the first r columns of U by Uj = \frac{1}{\sqrt \lambda_j}AVj . Since the Vj are orthogonal, so are the Uj. Since

image9357

Uj is a unit vector. If r < m, then we can expand U1, …, Ur to an orthonormal basis U1, …, Um for the set of m × 1 column vectors. In either case, let U be the m × m matrix whose columns are the Uj. Based on the construction described above, U is an orthogonal matrix.

Now let B = UTAV = [bij]. Then

image9359

for j ≤ r, and

image9360

for j > r. Let D = the m × n diagonal matrix whose main diagonal consists of \sqrt \lambda_1, …, \sqrt \lambda_rfollowed by zeros (if needed). We have just shown that UTAV = D, and so A = UDVT.

Observations

From the proof of the property, it follows that

image9361

Note that AAT = (AT)T(AT) is a positive semidefinite m × m matrix. In fact, we could have used AAT instead of ATA in the proof of Property 1. Also, note that

image9362

image9363

These are simply spectral decompositions of ATA and AAT. Note too that the diagonal matrix D2 for ATA is m × m, while the diagonal matrix D2 for AAT is n × n, but both have the same non-zero values on their main diagonals.

If A is a symmetric n × n matrix, then ATA = A2 = AAT and the two spectral decompositions can be considered equal with U = V. In fact, the singular value decomposition of A is then A = UDUT, which is the same as its spectral decomposition.

The columns of U corresponding to the non-zero diagonal elements form an orthonormal basis for the range of A, and so the rank of A = the number of non-zero diagonal elements. Thus a square matrix is invertible if and only if all the elements in D are positive. If A is invertible then A-1 = (UDVT )-1 = VD-1UT.

Solutions to Linear Equations

The solutions to the equation AX = C can be found as follows:

C = AX = UDVTX

and so

X = VD*UTC

Where D* is the diagonal matrix whose main diagonal consists of the reciprocals of the non-negative elements in D followed by zeros. We can view VD*UT as representing a sort of inverse for A even when A is not a square matrix.

The columns of V corresponding to the zero diagonal elements form an orthogonal basis for the null space of A, and so the dimension of the null space of A = the number of columns in A minus the rank of A, i.e. n–r in the proof of Property 1. Thus any linear combination of columns in V is a solution to the homogeneous equation AX = 0.

Note that AX = 0 if and only if AX = UDVTX = 0 if and only if

image9364

Thus X is a solution of AX = 0 if and only if X′ is a solution DX′ = 0 where X‘ = VTX. This means that λjX'_j = 0 for all j. But since the λj = 0 for j = r+1, …, n, it follows that X'_j = 0 for such j, and so Xj = VVTXj = VX'_j = 0. Thus if AX = 0 then X is a linear combination of the final n – r columns in V.

Since the λj = 0 for j = r+1, …, n, any linear combination of the final n – r columns in V is a solution to AX = 0. Since the columns of V are orthogonal and therefore independent, it follows that the final n – r columns of V form a basis for the null space, and so the dimension of the null space is n – r.

Worksheet Functions

Real Statistics Functions: The Real Statistics Resource Pack provides the following functions for the matrix in array or cell range R1:

SVD_U(R1, iter) = U matrix of the singular vector decomposition (SVD) for the matrix A corresponding to R1; thus A = UDVT where U and V are orthogonal matrices and D is a diagonal matrix.

SVD_D(R1, iter) = D matrix of the SVD for the matrix A corresponding to R1

SVD_V(R1, iter) = V matrix of the SVD for the matrix A corresponding to R1

Here iter is the number of iterations in the algorithm used to compute the SVD (default 200).

Example

Example 1: Find the Singular Value Decomposition for the matrix in range A1:D5 of Figure 1.

SVD example

Figure 1 – Singular Value Decomposition

The U, D and V matrices are displayed on the right side of Figure 1.

Clearly, D is a diagonal matrix. The array formulas

=MMULT(TRANSPOSE(F3:H5),F3:H5) =MMULT(F3:H5,TRANSPOSE(F3:H5))

produce an identity matrix, thus demonstrating that U is orthogonal. Similarly, we can demonstrate that V is an orthogonal matrix. The array formula =MMULT(F3:H5,MMULT(F8:I10,TRANSPOSE(F13:I16))) in range A8:D10 reproduces the original matrix, thus demonstrating that we have a singular value decomposition.

Data Analysis Tool

Real Statistics Data Analysis Tool: The SVD Factorization option of the Real Statistics Matrix Operations data analysis tool also provides the means to output the singular value decomposition of a square matrix.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Wikipedia (2013) Single value decomposition
https://en.wikipedia.org/wiki/Singular_value_decomposition

Golub, G. H., Van Loan, C. F. (1996) Matrix computations. 3rd ed. Johns Hopkins University Press

Searle, S. R. (1982) Matrix algebra useful for statistics. Wiley

Perry, W. L. (1988) Elementary linear algebra. McGraw-Hill

Fasshauer, G. (2015) Linear algebra.
https://math.iit.edu/~fass/532_handouts.html

Lambers, J. (2010) Numerical linear algebra
https://www.yumpu.com/en/document/view/41276350

28 thoughts on “Singular Value Decomposition”

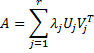
  1. Hi Charles !

    I’ve tried the SVD function and its work very well with smaller matrix like (2×3) matrix and so on. I also tried the SVD function on my matrix which is (18×21) matrix. I got U, sigma@D and V. But, when im trying to find check whether UDV’ = M, I got exacly the same output as M from Column 1 until 18 and #N/A for the last 3 column. UDV’ supposed to be (18×21) matrix just like M, but I cant figure out what is the problem.

    That’s my problem Mr Charles. Hopping you to help me.
    Thank you in advance.

    Reply

  2. Hi,
    I have a 2000*9 matrix. Can i do SVD using your add-in? Because when i was running it in excel the system was not responding.

    Reply

    • Hi Jacob,
      I don’t know whether SVD will work for this size of matrix. The SVD functions have only been tested for much smaller matrices,
      I am surprised that it doesn’t respond. Often this means that the processing is taking a long time. Have you tried to see whether it works for a smaller matrix?
      Charles

      Reply

  3. hi
    I downloaded this add-in and check the example you’ve done, but the output for U is just 0.873196379. just one number! and not a matrix. please advise me.
    thanks a lot
    Azi

    Reply

  4. Hi Charles,
    I’m trying to work out visualizing the geometric representation of the SVD in 3 dimensions. All of the reference material I have found states the usual information about the SVD taking matrix A and factoring it into matrices U, S, and V (transposed).
    They also portray these matrices as taking a circle or sphere, rotating it, scaling it into an ellipse or ellipsoid, and then rotating it again into it’s final position – the circle or sphere transformed by matrix A.

    I’m trying to replicate and visualize these matrix transforms, however I have used a few online SVD calculators and seem to be having problems getting the results of the SVD to comport with the geometric representation of the matrix A.

    I’m hoping that you might be able to give me some insight into what the problem or misunderstanding might be, and perhaps I can work out a visualization in EXCEL as well, using RealStatistics.

    http://news.povray.org/povray.binaries.images/message/%3Cweb.5dd33bd735e3eb74eec112d0%40news.povray.org%3E/#%3Cweb.5dd33bd735e3eb74eec112d0%40news.povray.org%3E

    Please feel free to email me if you need more information and the exact problems explained in greater detail. I was very happy to find your site, filled with excellent work by someone knowledgeable and genuinely interested in helping people understand a subject that they are obviously passionate about.

    Reply

    • Hello William,
      I have not really tried to look into this aspect of SVD. What problems are you encountering with getting the results of the SVD to comport with the geometric representation of the matrix A?
      Charles

      Reply

      • The axes I get from matrix V that correspond to the nonzero values in S don’t line up with the axes that the ellipsoid is scaled on.
        The diagrams and tutorials show U and V being purely rotational. Professor Todd Will said U and V are purely rotational. That would mean that they’d both be orthonormal and have determinants of 1. Only V/VT is orthormal with a determinant of 1.
        So when I apply UxSxVT, I don’t get the same results as applying matrix A.

        I’m also wondering about the magnitude of the singular values in S. Are they supposed to be equal to the scaling factors in A, or merely directly proportional? Otherwise I would expect that I’d see A = U x (S times some scalar) x VT.

        Reply

        • William,
          It would be easier for me to understand the situation with a specific example. Can you give me a simple example with real numbers that I can try out? Also what do you mean by V/VT (I understand that VT is the transpose of V)?
          Charles

          Reply

          • Sure, here’s 30 random vectors on the surface of an ellipsoid, derived from an anisotropically scaled sphere.

            The link I originally provided contains a larger data set and a link to an online SVD calculator I’ve tried using as well.

            0.0883597, -0.326943, -0.337204
            -0.405332, 0.103699, 0.242547
            0.421881, 0.0228523, -0.10112
            0.432184, 0.124463, -0.081805
            -0.397722, -0.42712, 0.00183197
            0.176067, -0.254352, -0.364851
            -0.0141579, 0.454459, -0.317524
            0.354473, 0.731663, -0.0403544
            0.188762, -0.165013, 0.215763
            0.267797, 0.895557, -0.10793
            -0.43112, -0.653533, 0.103569
            0.493277, 0.406603, -0.383698
            -0.168057, 0.047191, -0.251094
            -0.352057, 0.17805, 0.044775
            -0.0550539, -0.367475, -0.285988
            -0.00638087, 0.52994, 0.243583
            -0.349898, 0.134225, 0.0106983
            0.499981, 0.350186, -0.217316
            -0.23214, -0.569914, -0.129231
            0.312341, -0.220665, -0.321947
            -0.485278, -0.467105, 0.161888
            0.431548, 0.802902, -0.340641
            -0.321609, 0.0846096, -0.0622128
            -0.399561, 0.122994, 0.22922
            0.23747, -0.249359, -0.353554
            0.0726499, -0.337625, 0.295239
            -0.429676, -0.152071, 0.0678891
            0.352226, 0.220107, -0.462935
            0.506376, 0.337832, -0.278096
            -0.376505, -0.67281, 0.0373218

  5. Hi Charles,
    The function SVD returns only one value in excel, but as I understand U, V and D are matrices. Could you please with obtaining matrices?
    With kind regards,
    Medet

    Reply

  6. Thank you Charles for your prompt response, I was able to download it and successful installed it in my 2007 excel. I was also able to obtain the SVD of the matrix. Thanks again. Nice app

    Reply

  7. Please i need help to obtain the SVD of a 3by4 matrix.
    2 5 1 4
    4 3 2 2
    6 3 1 2
    I can’t find d the function in my version of excel. Any help will be appreciated.
    Onyx

    Reply

  8. SVD_U is sometimes giving #Value! It happened to many matrices I will give an example. Any help is greatly appreciated

    -0.088721917 -0.611548267 -0.962796502
    -5.647089783 -0.502167919 -0.79059257
    -3.790783085 -0.337095695 -0.530709632
    -2.34760153 -0.208760657 -0.328664214
    -1.431077773 -0.127258708 -0.200350888
    -0.907758067 -0.08072246 -0.127086129

    Reply

    • Rami,
      Perhaps you are using an old version of the Real Statistics software. In one of the last few versions I correction some error in the SVD_U function. The answer I get now for U is
      -0.037381909 -0.999301052 -9.10094E-09 2.98519E-10 -7.01112E-11 4.20293E-10
      -0.763403531 0.028557441 -0.018845734 -0.082496343 0.091553822 -0.071487468
      -0.512458152 0.019170063 0.018095374 -0.401453297 -0.322848265 -0.214276705
      -0.317361219 0.011871866 -0.013228788 0.874574071 -0.250001454 0.15765527
      -0.193460679 0.007236988 0.040372035 0.104632223 0.908208565 -0.018597225
      -0.122715547 0.00459055 0.012237016 -0.237069389 -0.006585681 0.961131622
      Charles

      Reply

  9. Thank you VERY MUCH for your e-mail reply with the attachment showing that SVD_U does indeed work properly on the example matrix. I went back to your website and downloaded the add-in anew to make sure I have the most current version. Voila, indeed, the SVD_U function works 🙂

    Reply

  10. SVD_U sometimes gives #VALUE! error. At first, I thought this only happened when U contained near zero values. Today, however, I found this same error on this simple matrix:
    1 16.85 1.46
    1 24.81 -4.61
    1 18.85 -0.21
    1 12.63 4.93
    1 21.38 -1.36
    1 18.78 -0.08
    1 15.58 2.98
    1 16.3 1.73
    This matrix is from this article on SVD and regression analysis:
    https://pdfs.semanticscholar.org/aef2/68c21be034bfd6228bf3946cb46e3c62cdb1.pdf
    The comparable SVDU function from the old Digilander site’s matrix.xla returns values without any problem (but I don’t like using it in today’s Excel – it was written for an older version and seems to cause some problems in current Excel). The Digilander site is no longer but it appears you can download the old matrix.xla here:
    http://www.bowdoin.edu/~rdelevie/excellaneous/#downloads
    I just mention matrix.xla in case it may be helpful in solving the problems with SVD_U

    Reply

    • Monte,
      The SVD_U function seems to work fine on this matrix and doesn’t return error values. I just tested it on my computer and will send you the results by email.
      Charles

      Reply

Leave a Comment