Basic Concepts
Generally to understand some characteristic of the general population we take a random sample and study the corresponding property for the sample. We then determine whether any conclusions reached about the sample are representative of the population.
This is done by choosing an estimator function for the characteristic (of the population) that we want to study and then applying this function to the sample to obtain an estimate. By using the appropriate statistical test we then determine whether this estimate is based solely on chance.
The hypothesis that the estimate is based solely on chance is called the null hypothesis. Thus, the null hypothesis is valid if the observed data (in the sample) do not differ from what would be expected based on chance alone. The complement of the null hypothesis is called the alternative hypothesis.
The null hypothesis is typically abbreviated as H0 and the alternative hypothesis as H1. Since the two are complementary (i.e. H0 is true if and only if H1 is false), it is sufficient to define the null hypothesis.
Caution
Since the sample usually only contains a subset of the data in the population, we cannot be certain as to whether the null hypothesis is true or not. We can merely gather information (via statistical tests) to determine whether it is likely or not. We therefore speak about rejecting or not rejecting (aka retaining) the null hypothesis based on some test, but not accepting the null hypothesis or the alternative hypothesis. Often in an experiment, we are actually determining the validity of the alternative hypothesis by testing whether or not to reject the null hypothesis.
Types of Error
When performing such tests, there is some chance that we will reach the wrong conclusion. In fact, here are two types of such errors:
- Type I – H0 is rejected even though it is true (false positive)
- Type II – H0 is not rejected even though it is false (false negative)
The acceptable level of Type I error is designated by alpha (α), while the acceptable level of Type II error is designated beta (β).
Significance
We use the following terminology:
Significance level is the acceptable level of type I error, denoted α. Typically, a significance level of α = .05 is used (although sometimes other levels such as α = .01 may be employed). In other words, we are willing to accept the fact that in 1 out of every 20 samples we reject the null hypothesis even though it is valid.
P-value (the probability value) is the value p of the statistic used to test the null hypothesis. If p < α then we reject the null hypothesis.
Critical region is the part of the sample space that corresponds to the rejection of the null hypothesis, i.e. the set of possible values of the test statistic that are better explained by the alternative hypothesis. The significance level is the probability that the test statistic will fall within the critical region when the null hypothesis is assumed to be true.
Usually, the critical region is depicted as a region under a curve for continuous distributions (or a portion of a bar chart for discrete distributions).
The typical approach for testing a null hypothesis is to select a statistic based on a sample of fixed size, calculate the value of the statistic for the sample, and then reject the null hypothesis if and only if the statistic falls in the critical region.
One-tailed tests
One-tailed hypothesis testing specifies the direction of the statistical test. For example, to test whether cloud seeding increases the average annual rainfall in an area that usually has an average annual rainfall of 20 cm, we define the null and alternative hypotheses as follows, where μ represents the average rainfall after cloud seeding.
H0: µ ≤ 20 (i.e. average rainfall does not increase after cloud seeding)
H1: µ > 20 (i.e. average rainfall increases after cloud seeding
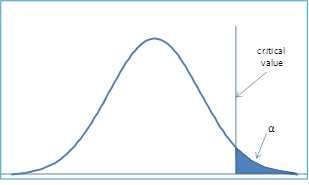
Here the experimenters are quite sure that the cloud seeding will not significantly reduce rainfall, and so a one-tailed test is used where the critical region is the shaded area in Figure 1. The null hypothesis is rejected only if the test statistic falls in the critical region, i.e. the test statistic has a value greater than the critical value.
Figure 1 – Critical region is the right tail
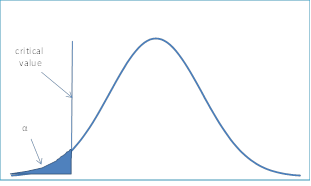
The critical value region here is the right (or upper) tail. It is quite possible to have one-sided tests where the critical region is the left (or lower) tail. For example, suppose the cloud seeding is expected to decrease rainfall. Then the null hypothesis would be as follows:
H0: µ ≥ 20 (i.e. average rainfall does not decrease after cloud seeding)
H1: µ < 20 (i.e. average rain decreases after cloud seeding)
Figure 2 – Critical region is the left tail
Two-tailed tests
Two-tailed hypothesis testing doesn’t specify the direction of the test. For the cloud seeding example, it is more common to use a two-tailed test. Here the null and alternative hypotheses are as follows.
H0: µ = 20
H1: µ ≠ 20
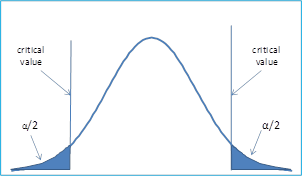
The reason for using a two-tailed test is that even though the experimenters expect cloud seeding to increase rainfall, it is possible that the reverse occurs and, in fact, a significant decrease in rainfall results. To take care of this possibility, a two-tailed test is used with the critical region consisting of both the upper and lower tails.
Figure 3 – Two-tailed hypothesis testing
In this case, we reject the null hypothesis if the test statistic falls on either side of the critical region. To achieve a significance level of α, the critical region in each tail must have size α/2.
Statistical power
Statistical power is 1 – β. Thus power is the probability that you find an effect when one exists, i.e. the probability of correctly rejecting a false null hypothesis. While a significance level for type I error of α = .05 is typically used, generally the target for β is .20 or .10, and so .80 or .90 is used as the target value for power.
Testing procedure
The general procedure for testing the null hypothesis is as follows:
- State the null and alternative hypotheses
- Specify α and the sample size
- Select an appropriate statistical test
- Collect data (note that the previous steps should be done before collecting data)
- Compute the test statistic based on the sample data
- Determine the p-value associated with the statistic
- Decide whether to reject the null hypothesis by comparing the p-value to α (i.e. reject the null hypothesis if p < α)
- Report your results, including effect sizes and confidence intervals
Caution
Suppose you perform a statistical test of the null hypothesis with α = .05 and obtain a p-value of p = .04, thereby rejecting the null hypothesis. This does not mean there is a 4% probability of the null hypothesis being true, i.e. P(H0) =.04. What you have shown instead is that assuming the null hypothesis is true, the conditional probability that the sample data exhibits the obtained test statistic is 0.04; i.e. P(D|H0) =.04 where D = the event that the sample data exhibits the observed test statistic.
References
Howell, D. C. (2010) Statistical methods for psychology, 7th Ed. Wadsworth. Cengage Learning
https://labs.la.utexas.edu/gilden/files/2016/05/Statistics-Text.pdf
Zar. J. H. (2010) Biostatistical analysis 5th Ed. Pearson
Generally, people have longer reaction times when naming incongruent colours. There are several theories the most common of which posits that the brain automatically reads words faster than it processes colour information.
The figure below shows the data from Stroop’s 1935 paper showing a sample of 100 students’ reaction times when they were shown a series of congruent (no interference) and incongruent (interference) words in random order.
The figure below shows the data from Stroop’s 1935 paper showing a sample of 100 students’ reaction times when they were shown a series of congruent (no interference) and incongruent (interference) words in random order.
What would be the most appropriate null hypothesis for testing whether there is a difference in reaction time between congruent and incongruent words?
Answer Options
a) H0: The mean reaction time for congruent colours is equal to the mean reaction time for incongruent colours.
b) H0: The mean reaction time for congruent colours is less than the mean reaction time for incongruent colours.
c) H0: The proportion of congruent colours is equal to the proportion of incongruent colours.
d) H0: The mean difference of reaction time between congruent and incongruent is nonzero.
This looks to be a homework problem. What is your question to me?
Charles
If something is hypothesised to have no correlation, but the correlation is found to be -.481 with a p-value of .010, was the hypothesis supported?
Hi Svetlana,
Usually, alpha = .05 is used as the significance level.
Since p = .01 is less than .05 = alpha, you have a significant result. This means that the null hypothesis is not supported.
If p-value = .10 then p = .10 > .05 = alpha, in which case the null hypothesis is supported.
Charles
HELP!!!!!
Imagine you conduct a single study and that the null hypothesis is really true for this study. You are about to conduct the analysis for this study. If you set α = .05 and calculate that β = .80, what is the likelihood that you will obtain statistically significant findings for this study?
Hello Michael,
Sorry for the delayed response. Have you already found the answer to your question? What motivates you to ask the question?
Charles
Power of the test is low, therefore not likely to yield reliable result.
Choose another evaluation method.
Please help me with this hypothesis question
Would it make sense in statistics for a company producing bleach to say their product (bleach) can kill all the germs that come into contact with the bleach?
It is hard to imagine any statistical way to demonstrate 100% effectiveness. Even after you have tested a very large sample and found that the product kills all the germs in each case, you still can’t conclude that it will be this effective in the next case (unless of course your sample was equal to the entire population, which would be impossible in this example).
You can say that the product is 100% effective with say 99% confidence, but that would be an assertion that would be difficult for most people to interpret.
Charles
Hi,
Great work on these tools.
I need to do a graphic in Excel to show the result of the T Test: Two Independent Samples, but I cannot to find a way to make a graph showing the t stat like the graphs than you painted on this tutorial.
Thanks you by your answer,
Martha
Hi Martha,
Are you trying to graph the t distribution. If so, create a table as follows where you can set df to any positive value that you want.
Cell A1: -5
Cell A2: A1+.2
Cell B1: =T.DIST(A1,df)
Now highlight the range A2:A50 and press Ctrl-D
Next highlight the range B1:B50 and press Ctrl-D
Finally, create an Excel scatter chart using the data in range A1:B50.
Charles
Which one to reject?
Whenever we state the null and the alternative hypothesis, is it always right to think that the alternative is “the one you actually want or hope to happen”, and the null “the one you want to reject”. For example, machine A produces gadgets and in a batch of 100, you know that 10% is defective.
Then, here comes a salesperson claiming that he can sell you another machine B where only 5% of the production is defective, so p=5%. Now you think he is just bluffing you, and you think that 10% is defective. Whatever!!!
So how should you set up the null and alternative hypothesis? Why did you choose to set it that way?
1. If 5% and 10% are the only possibilities, then you can use H0: p = 5% and H1: p = 10% or the version with the null and alternative hypotheses reversed. Which to choose is up to you and depends on why you are performing such a test at all.
2. The problem with either of these approaches is that there are many other possibilities (6%, 8%, etc.). You could determine which of 5% or 10% is more probable (although it could be that say 7.5% is more probable than either of these). This is not hypothesis testing per se, but it might be what you really want to know.
3. You could use H0: p <= 7.5% and H1: p > 7.5%
Charles
Looks like a lot of people don’t read comments and just go straight to asking for homework solutions. Just wanted to say this is a great article that has helped me to better understand “null” vs “alternative”, so thank you. Also that I appreciate your patience!
Logan,
Thank you for your comment.
Charles
Can i ask a question?
According to a university study, the mean charitable contribution per family among families with income of ₱50 000 or more in the Philippines in 2008 was ₱1 500. A researcher believes that the level of giving has changed since then. Determine the null and alternative hypotheses.
Bonso,
What do you think the null and alternative hypotheses are? Keep in mind that you usually choose as the alternative hypothesis the hypothesis that you hope is true.
Charles
Hi Charles,
I am trying to understand how would it be best for me to set as my Null and Alternative Hypothesis. My research is around air pollution, whereby I am trying to prove that the rise of pollutant A is due to biomass burning from X location.
My thoughts are:
Null: Rise of pollutant A is NOT from X location
Alternative: Rise of pollutant A is from X location
Am I doing this correctly?
Jaya,
This seems correct.
Charles
Hi Charles,
Thank you for the well thorough lesson you provided based on the null hypotheses and Alternative.
I Would appreciate it if you can clarify or confirm to me if I’m on the right track,
I performed a test of P-value to identify the relationship between the conservation practices in terms of purposes and services. The hypothesis is average scores should appear the same, meaning having the conservation purposes must have the same score as services, while performing the P-value it turns out this result as written below. Please can you help me with how to report this or put it into a proper report?
Note:
AV-SC-PUR- is the average score for purposes
AV-SC-SU- average score for services
Correlations
AV-SC-PUR AV-SC-SU
AV-SC-PUR Pearson Correlation 1 .500
Sig. (2-tailed) .500
N 4 4
AV-SC-SU Pearson Correlation .500 1
Sig. (2-tailed) .500
N 4 4
Without further information, I can’t say whether you have chosen the right test, although it seems like an appropriate test.
When there is a significant result, the reporting for such a test is as follows:
“A Pearson product-moment correlation was run to determine the relationship between height and distance jumped in a long jump. There was a strong, positive correlation between height and distance jumped, which was statistically significant (r = .706, n = 14, p = .005).”
This was taken from https://statistics.laerd.com/spss-tutorials/pearsons-product-moment-correlation-using-spss-statistics.php
Charles
Hi Charles,
I am struggling with finding a null hypothesis value required by a program for sample size calculation. The estimation of sample size is about a single proportion or a single mean. I’ve found that most formulas use proportion and Precision or Margin of Error (or mean and Precision or Margin of Error) for the inputs. This program I mentioned, requires a null hypothesis value instead of Precision or Margin of Error. I have no idea how I can come up with that number. Please suggest.
Thanks very much
Sorry Tina, but I don’t know why you would need to know the null hypothesis. Most programs that I am aware of require the effect size. If this can be determined from the null hypothesis, then all is good.
In any case, you need to know the null hypothesis before you can perform any statistical test, and so it doesn’t seem like a burden for you to know the null hypothesis.
Charles
I have a little bit hard time to understand null and alternative hypothesis
can you help me to compute null and hypothesis, is there a formula for these?
The null and alternative hypotheses are not computed. There are formulas for testing these hypotheses. The specific formulas depend on the specific test used.
Charles
Hello i need help in answering this problem and you please help me? Thank you in advance.
Suppose I told you that last night’s PBA game resulted in a score of 26 to 13. You
would probably decide that I had misread the paper, because basketball games almost
never have scores that low, and i was discussing something other than a basketball score.
In effect you have just tested and rejected a null hypothesis.
(A) What was the null hypothesis?
(B) Outline the hypothesis-testing procedure that you have just applied
Reyyan,
What sort of help do you need? What is your best guess as to what is the null hypothesis?
Charles
the mean life of battery used in digital clock is 305 days. the lives of batteries follow the normal distribution. the battery was recently modified with the objectives of making it last longer. a sample of 20 of the modified batteries had a mean life of 311 days with the standard deviation of 12 days. did the modification increase the mean life of battery
What is your question?
Charles
Hi Charles,
I would need a little help with finding what the null hypotheses and alternative hypotheses are. I am really lost. Please help.
text: Lucid dreaming is a unique phenomenon with potential applications for therapeutic interventions. Few studies have investigated the effect of lucidity on an individual´s waking mood, which could have valuable implications for improving psychological well being. the current experiment aims to investigate whether the experience of lucidity enhances positive waking mood, and whether lucidity is associated with dream emotional content and subjective sleep quality. 20 participants were asked to complete lucid dream induction techniques along with an online dream diary for one week, which features a 19-item lucidity questionnaire, and subjective ratings of sleep quality, dream emotional content, and waking mood. Results indicated that higher lucidity was associated with more positive dream and elevated positive waking mood the next day, although there was no relationship with sleep quality. the results of the research and suggestions for future investigations, such as the need for longitudinal studies of lucidity and mood, are discussed.
Lenka,
This webpage gives a number of examples of how to construct the null and alternative hypotheses. Generally, it is the alternative hypothesis that you believe is true and you want to collect evidence that supports the alternative hypothesis instead of the null hypothesis /which is the opposite of the alternative hypothesis). I suggest that you forget all about statistics for a moment and state in your own words what the study is trying to demonstrate. This will become the alternative hypothesis (often after stripping out some non-essential words).
Give it a try and let me know what you come up with. I can then comment further.
Charles
The psychological effect of stress and anxiety among college student.
what is the ho and ha?
This depends on what you want to test about stress and anxiety among college students. More details are needed to determine h0 and ha.
Charles
I have a problem I need help with.
Corporate HR has informed you that the average salary across all businesses in the holding company is $63,000. We are considering acquisition of a new company employing several thousand workers. HR sampled the salaries of 25 of those workers. Mean salary of the sample is $56,000. Sample standard deviation is $4,200.
1. You need to test whether the acquisition with upset salary equity. What are the null and alternate hypotheses?
2. Given the problem as stated, use the stepwise method to calculate the obtained t-value. report the results.
Joyce,
What sort of help do you need? Do you have some specific questions?
Charles
Hi Charles,
I am having difficulty deciding which hypothesis is the null hypothesis vs. the alternative hypotheses.
Above, you state that “The hypothesis that the estimate is based solely on chance is called the null hypothesis.”
Does this mean that the hypothesis that the estimator (typically a value or a proportion) is probably a result of the random sample and NOT indicative of a fundamental change in the data is always the null hypothesis?
If that’s true, then for any problem the null hypothesis would be the one that you are directly asked to test (i.e. the one that conforms to the population data).
Apologies if the question doesn’t make sense…
Fraser,
This is a good question.
Generally, you assume that you are dealing with a random sample (whether or not the null hypothesis is true). Usually, you make the hypothesis that you expect to be true (or the one that you hope to gather evidence for) to be the alternative hypothesis. Thus, your goal is to disprove the null hypothesis (here “disprove” really means “show to be unlikely”). E.g. if I want to show that it rains more on Sunday than on Monday, then my alternative hypothesis is that it rains more on Sunday than Monday (H1: S > M) and so my null hypothesis is it rains no more on Sunday than on Monday (H0: M <= S). Now, I collect data and I see that of the 1,000 Sundays and Mondays I pick at random, it rains on Sunday 100 times and it rains on Monday 95 times. Clearly, in my sample, it rains more on Sunday than on Monday, but I need to be careful not to conclude that this shows that the alternative hypothesis is true. In fact, if you do the statistical analysis (using the binomial distribution), you will see that even if the null hypothesis were true the outcome that you see from the sample is not so uncommon (i.e. it can occur by chance even if the null hypothesis were true and the alternative were false). If in the experiment, instead, it rains 100 times on Sunday and 75 times on Monday, you would reach a different conclusion since this level of difference is much more unlikely if the null hypothesis were true (in fact p-value = .035 < .05 = alpha). You would conclude that this result is probably not by chance, but is due to the alternative hypothesis likely being true. Charles
Hi, can you help me in this problem?
Two rival manufacturers of penlight batteries claimed that their product lasts longer than the other. Thirty samples of Brand A and thirty-four of Brand B were tested. The following are the lengths of lives of such batteries recorded in hours.
Brand A
38
41
42
36
39
42
43
35
36
38
42
39
40
43
44
35
40
39
37
41
40
44
38
37
41
40
38
42
45
41
Brand B
38
40
41
43
39
41
40
43
39
38
40
43
44
39
40
41
42
39
40
45
40
38
42
41
40
36
37
41
42
40
36
38
41
40
Using 0.05 level of significance, test if there is a significant difference in the length of life of the two brands of penlight batteries.
This looks like a homework problem. I have a policy of not doing homework problems, but I am happy to answer questions. What questions do you have that will help you with this problem.
Charles
the hypothesis, the confidence level criteria and the decision rule
Sorry Faye, but I don’t understand your question or comment.
Charles
The problem needs the null and alternative hypothesis, the confidence level criteria and the decision rule
Faye,
What do you think the null hypothesis should be? (Even if you are not sure, what is your best guess?) What test do you think would be appropriate?
Charles
2. “Reader’s Corner” is a famous book store in NCR. The store sells all type of books and has a large customer base. The management of Reader’s Corner perceives that on an average, post graduates spend more money on purchase of books as compared to graduates who visit their store. In order to validate this claim, the management conducted a survey and the following results were obtained.
State the null and alternate hypothesis
This looks like a homework assignment. I have a policy of not doing students’ homework, although I am willing to point you in the correct direction. What sort of problem are you having in answering the question yourself?
Charles
Hi Charles,
I was doing an exercise where an answer was provided but I am not 100% sure whether the answer is correct.
Question:
“Assume that consumer regulations specify that all marketed confectionery products should have a target weight of at least the advertised weight (in this case 100 grammes per bar).
Write a Null and Alternative Hypothesis to test if the sample of 60 chocolate bars implies the population of bars meets the consumer regulations (i.e. 100 grammes weight or more for these bars) ”
Answer given:
Null Hypothesis (Ho): μ 100 g
With my understanding is the null hypothesis should be (Ho): μ >= 100 g as the question states that the bars should be at least 100grammes (100g+).
Am I interpreting the question incorrectly?
Greatly appreciate it if you can shine some light on this.
-Melody
it seems partial of the answer given was cut off
answer given:
((H0): μ100g
Hello Melody,
Usually, you try to disprove the null hypothesis. Thus,
Ho: μ < 100 g H1: μ >= 100 g
Charles