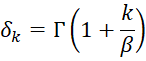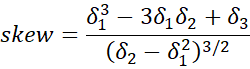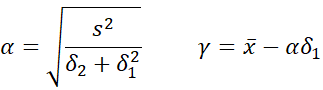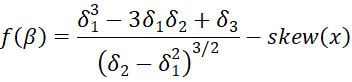Objective
We describe how to use the method of moments to fit a 3-parameter Weibull distribution to a dataset.
Approach
If we define
then as we have seen in Three-Parameter Weibull Distribution, it follows that
For the method of moments, once you calculate β from the skewness, using Newton’s method, you can obtain the values for the other two parameters via
where x̄ and s2 are the sample mean and variance, respectively.
Example
Example 1: Use the method of moments to fit the data in column A of Figure 1 to a three-parameter Weibull distribution.
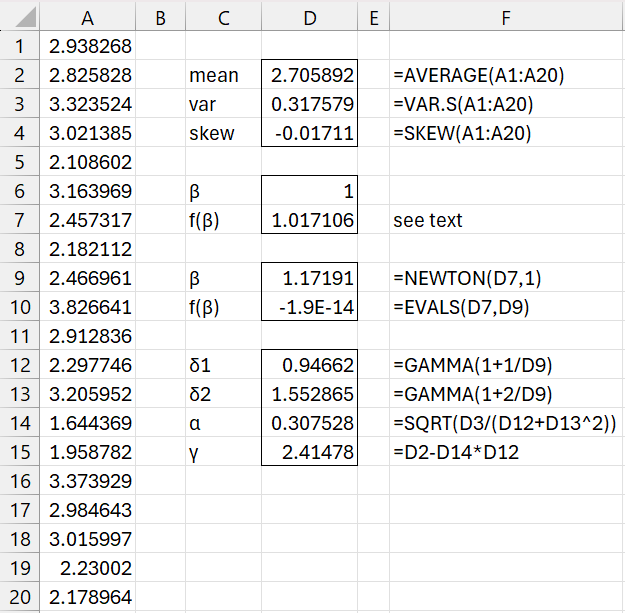
The analysis is shown in Figure 1.
Figure 1 – Fitting the data via MoM
We use Real Statistics NEWTON function to solve the equation f(β) = 0 where
and skew(x) = the skewness of the sample data, which is -.1711 as shown in cell D4. Here, cell D7 contains the formula
=(GAMMA(1+1/D6)^3-3*GAMMA(1+1/D6)*GAMMA(1+2/D6)+ GAMMA(1+3/D6))/(GAMMA(1+2/D6)-GAMMA(1+1/D6)^2)^(3/2)-D$4
Using the lambda formula =NEWTON(D7,1), we see that f(β) = 0 when β = 1.7191 (cell D9). This results in α = 3.07528 and γ = 2.41478.
So far, so good. The problem, however, is that the location parameter γ must be less than all the data elements in the sample, namely γ ≤ min(A1:A20) = 1.644369. Since this not the case, the result is not viable.
Alternative Approach
In Fitting 3-Parameter Weibull Distribution using MLE we describe an approach for fitting a 3 parameter Weibull distribution by optimizing the gamma value that provides the best fit. We describe both an MLE and MoM version of this approach.
In addition, we describe the WEIBULL3_FITM worksheet function.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Wikipedia (2021) The Weibull distribution
http://reliawiki.org/index.php/The_Weibull_Distribution
Cousineau, D. (2008) Fitting the three-parameter Weibull distribution: review and evaluation of existing and new methods
http://www.mapageweb.umontreal.ca/cousined/home/others/distrifitting/docs/31_fitweibull_vieee_vproofs.pdf