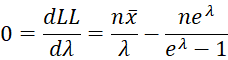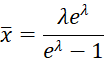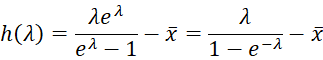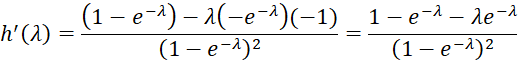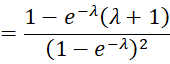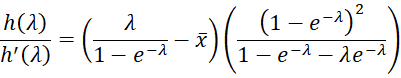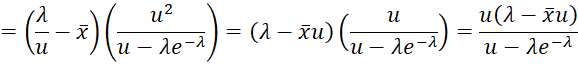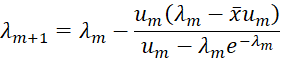Fitting Zero-Truncated Poisson Distribution

Basic Concepts

The Zero-Truncated Poisson (ZTP) distribution is characterized by the λ parameter which is the mean of the corresponding non-truncated Poisson distribution. We can use the mean of a sample, x1, .., xn (taking non-negative integer values only) to create an estimate of the lambda parameter using the MLE approach.

MLE Steps

The log-likelihood function for the ZTP distribution is

Equivalent LLAnother equivalent LL

To maximize LL, we set the first derivative to zero.

First derivative of LL

Solving for the mean of the sample, we get

Mean of the sample

This is the same expression for the mean as shown in Zero-Truncated Poisson Distribution. Thus, the method of moments and the MLE fitting method produce the same result.

Newton’s method

In any case, we can use Newton’s method to estimate λ. This is done by first defining h(λ) as follows.

h(lambda) function

We now estimate the value of lambda for which h(λ) = 0. The derivative of h is

Derivative of h

h'(lambda)

It now follows that

h(lambda)/h'(lambda)

Equivalent formula

where u = 1 – e-λ. Thus, we can estimate λ using Newton’s method via the iteration

Newton's method iteration

Example

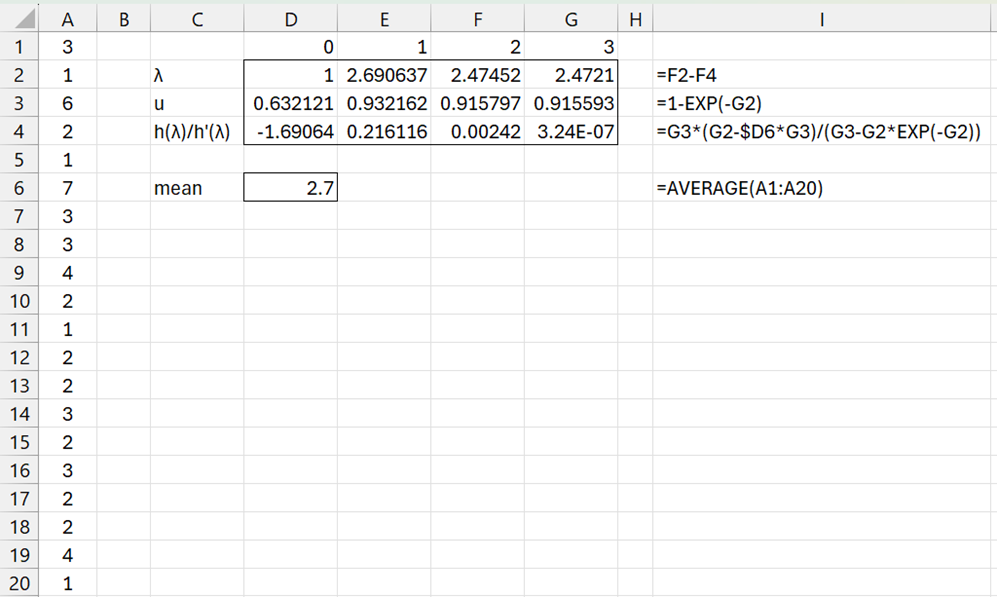
Example 1: Determine the best ZTP fit for the data in column A of Figure 1.

ZTP fit example

Figure 1 – Fitting a ZTP distribution

We see that convergence is relatively quick based on an initial guess of λ = 1 (in cell D2).

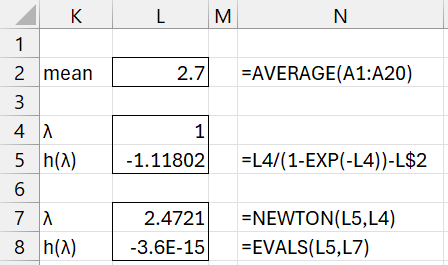
We arrive at the same estimate for lambda by using Real Statistics’ NEWTON worksheet function (see Root-finding Functions), as shown in cell L7 of Figure 2.

Estimate using NEWTON function

Figure 2 – ZTP estimate using NEWTON function

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

Reference

Wikipedia (2025) Zero-truncated Poisson distribution
https://en.wikipedia.org/wiki/Zero-truncated_Poisson_distribution

Leave a Comment