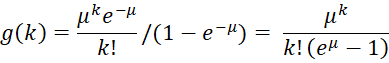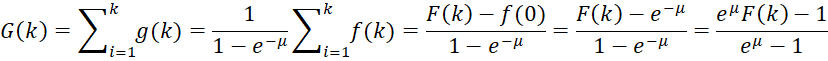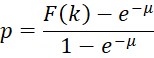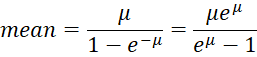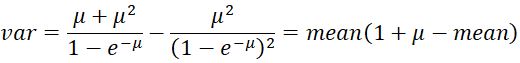Basic Concepts
A Zero Truncated Poisson (ZTP) distribution is a Poisson distribution where zero counts are not possible. This is the distribution with probability density function (pdf)
g(k) = P(x = k | x > 0) = f(k)/(1–f(0))
where f(k) is the usual Poisson pdf. Thus, the pdf is
The cumulative distribution function (cdf) is therefore
where F(k) is the usual Poisson cdf.
We can calculate the inverse cdf as follows:
Solving for F(k), we get
It now follows that
Properties
The mean and variance of this distribution are
Worksheet Functions
The Real Statistics Resource Pack provides the following two worksheet functions.
TPOISSON_DIST(x, μ, cum) = the probability density function value g(x) for the Poisson distribution with rate parameter μ if cum = FALSE, and the corresponding cumulative probability distribution value G(x) if cum = TRUE.
TPOISSON_INV(p, μ) = smallest integer x such that POISSON(x, μ, TRUE) ≥ p
You can generate a random value from this distribution by using the formula
=TPOISSON_INV(RAND(), μ)
References
Wikipedia (2025) Zero-truncated Poisson distribution
https://en.wikipedia.org/wiki/Zero-truncated_Poisson_distribution