Objective
We have two goals:
- determine the minimum effect size required to achieve a given level of support for the alternative (or null) hypothesis for a given sample size
- determine the minimum sample size required to achieve a given level of support for the alternative hypothesis for a given effect size
We will use the terminology described in Bayesian Hypothesis Testing and Bayesian t Test Tools.
Approach using Goal Seek
Example 1: Find the effect size δ for a one-sample t-test with n = 16, using the JZS prior with default scale that results in substantial support for the alternative hypothesis.
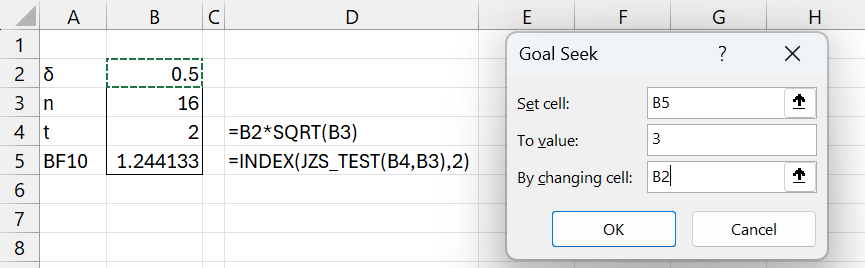
We start by creating the worksheet shown on the left side of Figure 1.
Figure 1 – Calculating the effect size
We see that if n = 16 and effect size δ is .5 (a medium effect), then BF10 = 1.244, which shows very weak support (“barely worth mentioning”) for the alternative hypothesis. To determine the value of δ for which BF10 = 3 (the threshold for substantial support), we use Excel’s Goal Seek capability as displayed on the right side of Figure 1.
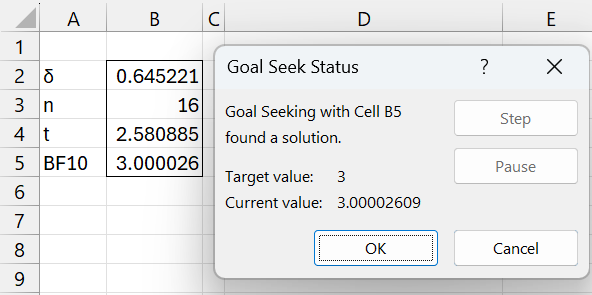
When we click on the OK button, the worksheet changes to that shown in Figure 2.
Figure 2 – Finding the effect size
We see that an effect size of .645221 is required to obtain substantial support for the alternative hypothesis.
If we can use Goal Seek in the same way to determine the minimum value of δ to achieve solid support for the alternative hypothesis (BF10 = 10), namely δ = .825424 (large effect).
Example 2: What is the minimum sample size required to achieve strong evidence (BF10 = 10) for the alternative hypothesis for a medium effect size (δ = .5)?
This time, we insert 10 in the To Value field and B3 in the By changing cell field in the dialog box in Figure 1. We obtain a sample size of 38.60914, and so a sample of size 39 is required.
Worksheet Functions
The Real Statistics Resource Pack provides the following worksheet functions:
JZS_EFFECT(bf, n1, n2, scale, iter) = minimum value of the effect size δ for a t-test using a JZS prior with the specified scale (default √2/2). If n2 = 0 (default), then a single sample of size n1 is considered; otherwise, two samples of sizes n1 and n2 are considered.
JZS_SIZE(bf, effect, , scale, iter) = minimum size for which BF10 ≥ bf for a one-sample t-test with the specified effect size using a JZS prior with the specified scale (default √2/2).
JZS_SIZE(bf, effect, ratio, scale, iter) = minimum size for which BF10 ≥ bf for a two-sample t-test with the specified effect size using a JZS prior with the specified scale (default √2/2). Here, the size of the second sample equals the size of the first sample times ratio (the samples have the same size when ratio = 1).
If ratio is a negative number, then the second sample has ratio fewer elements than the first sample. If ratio is zero, then we use the one-sample version of the function.
iter is used to compute the integral (default 10000).
The worksheet functions BayesT_EFFECT(bf, n1, n2, scale) and BayesT_SIZE(bf, effect, ratio, scale) are also available. These are defined as above based on a t-test using a weakly informational normal prior.
The Real Statistics Resource Pack also provides the BayesT0_EFFECT(odds, n1, n2) and BayesT0_SIZE(odds, effect, ratio) worksheet functions. These are defined as above based on a t-test using a Jeffreys’ non-informational prior, where Odds10 ≥ odds is used instead of BF10 ≥ bf.
One sample examples
We can obtain the results for Examples 1 and 2 as follows:
JZS_EFFECT(3,16) = .64522
JZS_EFFECT(10,16) = .825425
JZS_SIZE(10,.5) = 38.60915
We can also determine the minimum effect size required for very strong support for the alternative hypothesis using a t-test on a sample of size 25.
JZS_EFFECT(30,25) = .735743
For decisive support, we can use
JZS_EFFECT(100,25) = .735743
The sample size required for very strong support for an effect size of .5, we use
JZS_SIZE(30,0.5) = 49.58
You can also use JZS_EFFECT and BayesT_EFFECT to determine support for the null hypothesis. For example, JZS_EFFECT(1/3, 25) = .201817 shows that a small effect can be determined with substantial support for the null hypothesis with a sample of size 25.
JZS_SIZE, BayesT_SIZE, BayesT0_SIZE, and BayesT0_EFFECT, however, can only be used when bf > 1 (or odds > 1).
Finally, note that critical t-stat values can be determined by using the formula
JZS_EFFECT(bf, n, , scale, iter)*SQRT(n)
Two sample examples
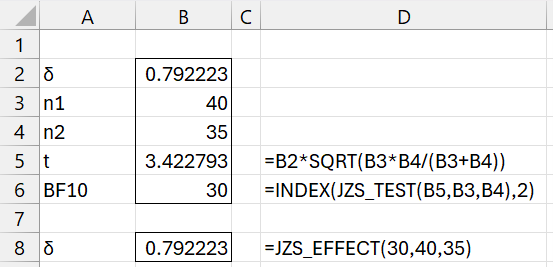
What is the minimum effect size required to obtain very strong support for the alternative hypothesis using a two-sample test with 35 and 40 elements?
We see from Figure 3 that the minimum effect size is .792223.
Figure 3 – Effect size for two-sample t-test
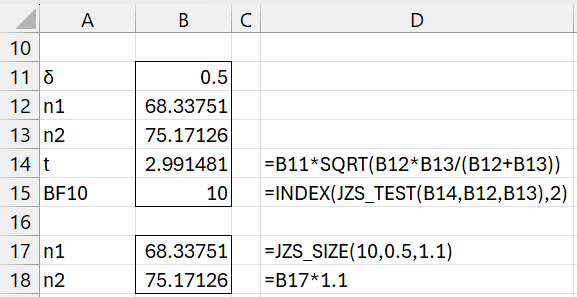
What is the minimum sample size required to provide strong support for the alternative hypothesis for a medium effect size, assuming that the one sample is 10% larger than the other.
We see from Figure 4 that the required sample sizes are 68.33751 and 75.17126.
Figure 4 – Sample size for a medium effect size
Using the formula =JZS_SIZE(10,.5,1), if the samples have the same size, then samples of size 71.59604 are required.
Finally, if you want one sample to be one element smaller than the other, then you can use the formula =JZS_SIZE(10,.5,-1) to obtain the value 72.09944, which implies that the samples have size 72.09944 and 71.09944.
Effect Size and Sample Size Tables
Click here for access to the tables of effect sizes and sample sizes for the Bayesian t-test.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Reich, B. J., Ghosh, S. K. (2019) Bayesian statistics methods. CRC Press
Gronau, Q. F., Ly, A., Wagenmakers, E-J. (2018) Informed Bayesian t-tests
https://arxiv.org/pdf/1704.02479
Gonen, M., Johnson, W. O., Lu, Y., Westfall, P. H. (2005) The Bayesian two-sample t test. The American Statistician, 59(3):252–257.
https://scispace.com/pdf/the-bayesian-two-sample-t-test-2cf8tnzpmi.pdf