Example 1: Repeat Example 1 of Two Binomial Samples Beta Prior using the Metropolis algorithm described in Random Walk Metropolis Algorithm.
We proceed as in Example 1 of Random Walk Metropolis Algorithm, except that now we use a bivariate normal distribution as our proposal distribution. In particular, we use a bivariate normal distribution with standard deviation .1 for both dimensions and 0 correlation. We can use the formula =BNORMDIST(x1,x2,m1,m2,s1,s2,r,TRUE) to compute the value of the bivariate normal distribution. Since the correlation r is zero, we can use the following formula instead:
=NORM.DIST(x1,m1,s1,TRUE)*NORM.DIST(x2,m2,s2,TRUE).
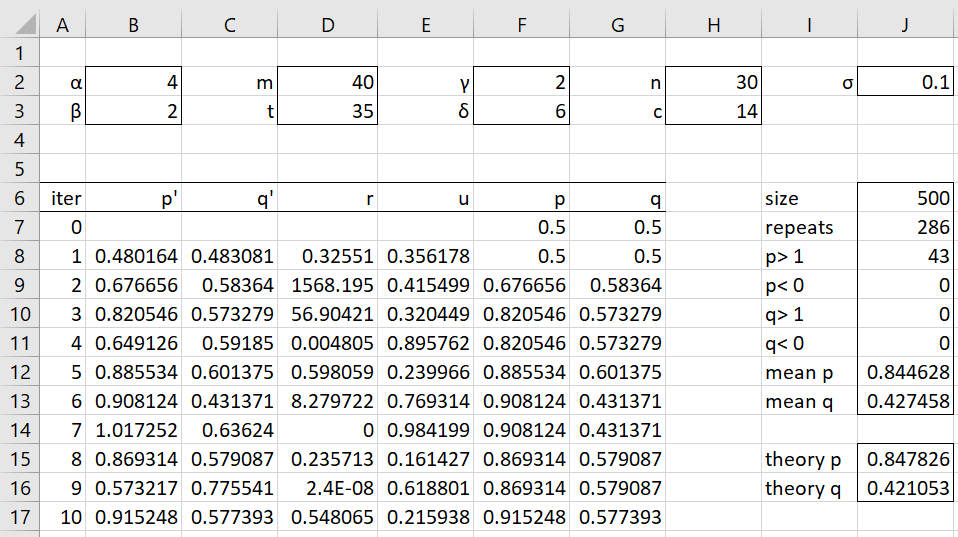
The results, using a very small sample of 500 elements, is shown in Figure 1. The mean p = .850629 and q = .424495 is pretty close to the theoretical mean values p = α/(α+β) and q = γ/(γ+δ) of the posterior beta distributions, as shown in cells J15 and J16.
Figure 1 – Metropolis algorithm
Key formulas from Figure 1 are shown in Figure 2.
Figure 2 – Key formulas from Figure 1
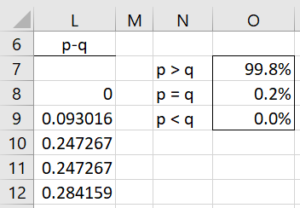
If we look at the 500 sample values of p–q (see Figure 3, which only shows the first 5 values), we see that except for the first value, for all the others p > q, which again gives us a high degree of confidence that the drug is effective. Here, cell O7 contains the formula =COUNTIF(L8:L507,”>0″)/$J$6.
Figure 3 – p minus q