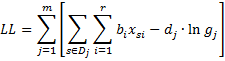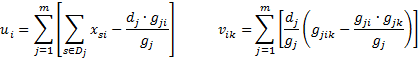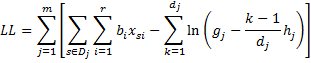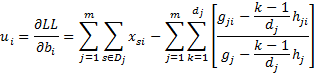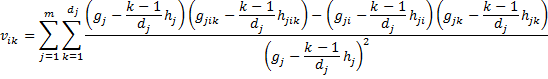Cox Regression Models with Multiple Deaths per Time Period

Basic Concepts

In Cox Regression using Newton’s Method, we described how to calculate LL, the regression coefficients, the standard errors of these coefficients and some other statistics in the case where d_j = 1 for each j, i.e. where there is exactly one death per time interval.

This is a reasonable assumption if we view time as a continuum since it is unlikely that two deaths will occur at exactly the same moment in time. If, however, we view time in discrete units, as is commonly done, then we need to revise the formula used for LL described in Cox Regression using Newton’s Method.

If we drop the d_j = 1 assumption, then two commonly used approximations for the partial likelihood function (see Cox Regression Model Fit) are employed: Breslow’s approximation and Efron’s approximation. The second is more accurate, although the first is very commonly used.

We now describe these two approaches, using the terminology employed in Cox Regression using Newton’s Method.

Breslow’s approximation

We use the following approximations

Efron’s approximation

We use the following approximation

where

Newton’s Method

We can use these values with Newton’s Method as described in Property 1.

Property 1 (Newton-Raphson): We can estimate the r × 1 coefficient matrix B = [b_i] as B_p for some large enough p, where B₀ consists of all zeros (initial guess) and for all p

where  = [v_ik] is the r × r (information) matrix and U_p = [u_i] is the r × 1 (score) matrix where we use the coefficients b₁, …, b_r in B_p in calculating u_i and v_ik.

In addition, I_p is the covariance matrix for B_p at each step p in the iteration.

References

NCSS (2015) Cox regression
https://www.ncss.com/wp-content/themes/ncss/pdf/Procedures/NCSS/Cox_Regression.pdf

Collett, D. (2003) Modelling survival data in medical research. 2nd ed. Chapman & Hall/CRC

Borucka, J. (2014) Methods for handling tied events in the Cox proportional hazard model
https://bazekon.uek.krakow.pl/gospodarka/171291373