We begin by investigating the saturated model, which accounts for all the possible variables. We do this by reexamining Example 2 of Independence Testing using a log-linear approach.
Example
Example 1: Create a saturated log-linear model for the data in Example 2 of Independence Testing
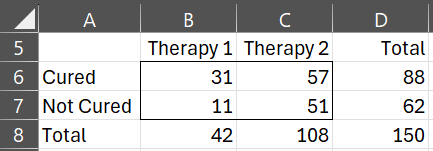
The data for the 150 patients are again summarized in the contingency table in Figure 1.
Figure 1 – Contingency table
Define the following coding of the categorical variables:
t1 = 1 if therapy 1 and = -1 if therapy 2
t2 = 1 if cured and = -1 if not cured
Based on this coding the data can be expressed as in Figure 2.
Figure 2 – Fitting the data to the saturated model
The log-linear model takes the form:
ln yi = β0 + β1ti1 + β2ti2 + β3ti1ti2 + ln εi
Here all the variables are included, including the interaction terms. This is called the saturated model. We now find the values of the population coefficients β0, β1, β2, β3. As usual, using the sample data we find the estimates of these coefficients b0, b1, b2, b3, where
ln yi = b0 + b1ti1 + b2ti2 + b3ti1ti2
It then follows (using the data in Figure 2) that:
3.434 = ln 31 = ln y1 = b0 + b1⋅1 + b2⋅1 + b3⋅1 = b0 + b1 + b2 + b3
2.398 = ln 11 = ln y2 = b0 + b1⋅1 + b2(-1) + b3(-1) = b0 + b1 – b2 – b3
4.043 = ln 57 = ln y3 = b0 + b1(-1) + b2⋅1 + b3(-1) = b0 – b1 + b2 – b3
3.932 = ln 51 = ln y4 = b0 + b1(-1) + b2(-1) + b3⋅1 = b0 – b1 – b2 + b3
Adding all four equations and dividing by 4 we get
b0 = (ln 31 + ln 11 + ln 57 + ln 51)/4 = (3.434 + 2.398 + 4.043 + 3.932)/4 = 3.452
Adding the first two equations and dividing by 2 we get
b1 = (ln 31 + ln 11)/2 – b0 = (3.434 + 2.398)/2 – 3.452 = -.536
Now, adding the first and third equations and dividing by 2 we get
b2 = (ln 31 + ln 57)/2 – b0 = (3.434 + 4.043)/2 – 3.452 = .287
Adding the first and last and dividing by 2 we get
b3 = (ln 31 + ln 51)/2 – b0 = (3.434 + 3.932)/2 – 3.452 = .231
Thus the model is
ln y = 3.452 – .536 t1 + .287 t2 + .231 t1t2
which is equivalent to
y = exp(3.452 – .536 t1 + .287 t2 + .231 t1t2)
which is, in turn, is equivalent to
![]()
Using , the log-linear model takes the form (dropping the error term):
![]()
Marginal averages
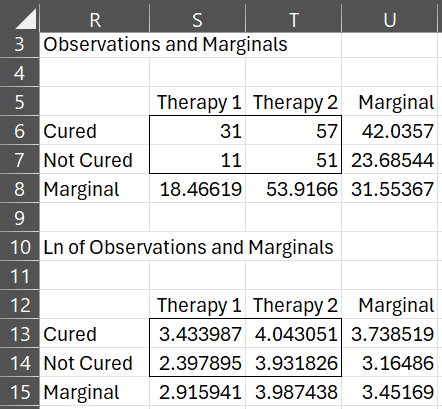
In Figure 3 we provide the contingency table for the logs of the original data in range S13:T14, but this time instead of calculating the marginal totals, we calculate the marginal averages.
Figure 3 – Marginal averages
Thus, for example, the marginal average for the Cured row (cell U13) contains the formula =AVERAGE(S13:T13) and the marginal average for the Therapy 1 column (cell S15) contains the formula =AVERAGE(S13:S14).
Note that b0 = the grand mean (cell U15), b1 = the mean for Cured (cell U13) minus the grand mean, b2 = the mean for Therapy 1 (cell S15) minus the grand mean and b3 = Cured × Therapy 1 (cell S13) minus the mean for Cured minus the mean for Therapy 1 plus the grand mean.
We now map the log values back into the original contingency table (range R5:U8) by using the exponential function. Thus the marginal average for the Cured row in the original contingency table (cell U6) is EXP(U13) = EXP(3.738519) = 42.0357. Note, however, that the arithmetic mean of 31 and 57 is not 42.0357. It turns out, however, that the geometric mean of 31 and 57 is 42.0357. Thus we could also put the formula GEOMEAN(S6:T6) in cell U6 and get the same value of 42.0357. This relationship is also true for the other marginal averages.
Observation
The saturated model is an exact fit for the data (i.e. the error terms are zero), and simply provides a new way of looking at the observed data.
The exact version of the coefficients calculated depends on the coding of the dummy variables used. E.g., if we use the coding
t1 = 0 if therapy 1 and = 1 if therapy 2
t2= 0 if not cured and = 1 if cured
then the log-linear regression model becomes:
ln y = 2.398 + 1.534 t1 + 1.036 t2 – .925 t1t2
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
Howell, D. C. (2010) Statistical methods for psychology (7th ed.). Wadsworth, Cengage Learning.
https://labs.la.utexas.edu/gilden/files/2016/05/Statistics-Text.pdf

Dear Charles,
maybe I found two small typos in your example 1 description:
1) In the set of equations for solving b coefficients, there should be ln y1, ln y2, ln y3, ln y4; instead of ln y1, ln y2, ln y2, ln y2
2) In the summary model for y (and ln y), there is additional index /1/ after the coefficient in the term for t_1; the same is also in the Marginal example.
Your big fan Jirka
My error:
in the 2) the same typo is not in the Marginal example, but in Observation
Dear Jirka,
Thank you for identifying these errors. I believe that I have now corrected the mistakes that you have found.
I appreciate your support and your help in improving the website.
Charles
You are wellcome, but one _1 index is still left in the equivalent model formulation y = e^…
Thanks Jirka for catching this error too. I just corrected the error on the webpage.
Charles
What is the criteria of stating that the Saturated model has the best fit?
As explained on the webpage, the saturated model is an exact fit for the data (i.e. the error terms are zero), and simply provides a new way of looking at the observed data. The saturated model is not only the “best fit”, it is an “exact fit”, in that it simply re-expresses the data exactly.
Charles
Hi, what if one of the variables (t3) is COntinuous Numeric?
Dominic Joseph,
In that case, we wouldn’t have a contingency table and the model would be completely different.
Charles
Thank you for your website – it is most helpful! I am having trouble understanding the log-linear regression model with the alternate coding at the bottom of the page. I would think that b0 = 3.932 (ln 51, when t1 = t2 = 0), which gave me the following model: ln y = 3.932 – 1.534 t1 + 0.111 t2 + 0.925 t1t2.
Thanks for your comment. The coding I actually used is
t1 = 0 if therapy 1 and = 1 if therapy 2 (instead of 1 for therapy 1 and 0 for therapy 2 which is how it was stated)
t2 = 0 if not cured and = 1 if cured
The probably accounts for the difference. I have now corrected the webpage.
Charles