Basic Concepts
The model for (A, B, C) is ln y = λ + λA + λB + λC and has abc – [(a – 1) + (b – 1) + (c – 1) + 1] = abc – (a+b+c) + 2 degrees of freedom. For Example 1 of Three-way Contingency Tables the mutual independence model has 2 ∙ 2 ∙ 3 – (2 + 2 + 3) + 2 = 7 degrees of freedom.
In this model A and B are independent, A and C are independent, and B and C are independent. The probability that an observation will occur in cell ijk is
Example
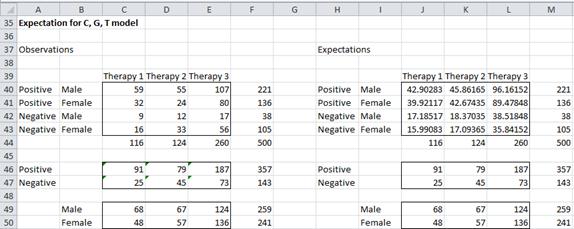
For Example 1 of Three-way Contingency Tables, the expected frequencies for the mutual independence model are given in Figure 1.
Figure 1 – Expected frequencies for (C, G, T) model
Once again, all the marginal totals for the expectations are set equal to the corresponding totals for the observations. Each of the cells in the range J40:L43 are calculated as described above. For example, the expected frequency of a positive result for males taking therapy 1 (cell J40) is calculated via the formula =M46*M49*J44/M44^2.
χ2 (maximum likelihood) is 64.48 with 7 degrees of freedom, which is significant, and so once again this model is not a good fit for the data.
Note too that
for any values of i, j, k, i′, j′, k′. E.g. the formula =(J40*K41)/(J41*K40) has value 1.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
Howell, D. C. (2010) Statistical methods for psychology (7th ed.). Wadsworth, Cengage Learning.
https://labs.la.utexas.edu/gilden/files/2016/05/Statistics-Text.pdf