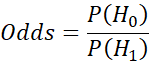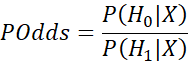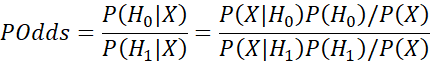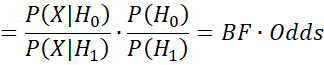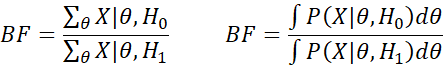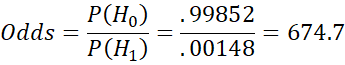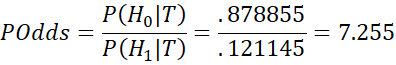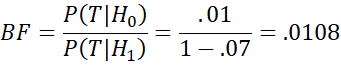Bayesian Hypothesis Testing | Real Statistics Using Excel

Basic Concepts

Hypothesis testing consists of determining whether the null hypothesis H₀ is more likely or less likely than an alternative hypothesis H₁ and by how much. Before we collect data, we compare P(H₀) with P(H₁) based on our prior beliefs as described by the prior probability functions for each hypothesis. We define the prior odds by

Once we have collected some data X, we can compare the posterior probabilities. Based on these, we can define the posterior odds by

Using Bayes Theorem, it follows that

Bayes Factor

Thus, the posterior odds are equal to the Bayes Factor (BF) times the prior odds, where the Bayes Factor is the ratio between the likelihood functions, i.e. BF compares the evidence between the two hypotheses.

When the hypotheses involve a parameter (or a number of parameters), then BF is a ratio of the marginal probabilities, and so BF is defined in the discrete and continuous cases by

Thus, BF takes into consideration all possible values of the parameters (based on each hypothesis).

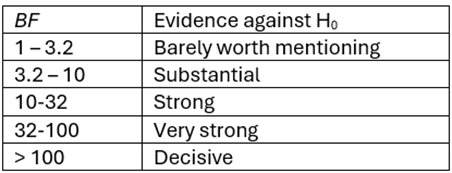
Figure 1 shows a way of evaluating the Bayesian Factor as a substitute for evaluating p-values in frequentist statistics. There are various alternative versions of this table.

Figure 1 – Interpreting the Bayes Factor

Example

Example 1: Let’s revisit Example 1 of about HIV testing, and in particular let’s consider the patients that tested positive for the virus. We will test the hypothesis that the patient doesn’t have HIV (hypothesis H₀) vs. the patient does have HIV (hypothesis H₁).

The prior probabilities are P(H₁) = .00148 and so P(H₀) = 1 – .00148 = .99852. Thus, the prior odds are

This means that prior to obtaining any test results it is 674.7 times more likely that a patient doesn’t have HIV (hypothesis H₀) than the patient has HIV (hypothesis H₁).

Now let T represent the event that the test is positive. In Example 1, we found that P(H₁|T) = .121145 and so P(H₀|T) = 1 – .121145 = .878855 (see Bayesian Example). Thus, the posterior odds are now