Objective
A major component of the strategy for winning at Wordle is to make a good initial guess. One approach is to pick a 5-letter word with letters that occur most frequently in the Wordle dictionary.
Letter Frequency
If we simply look at the letters used in the 2,315 possible target words shown on the Wordle Strategy webpage, we see the following distribution of letters of the alphabet:
Figure 1 – Letter frequency
We see from Figure 1 that “e” is the letter that is most frequently used (1,233 times in total), followed by “a”, “r”, “o”, “t”, “l”, “i”, “s”, “n”, “c”. The most frequently used letter in the first position is “s”, while the most frequently used letter in the second or third position is “a”. The most frequently used letter in the fourth or fifth position is “e”.
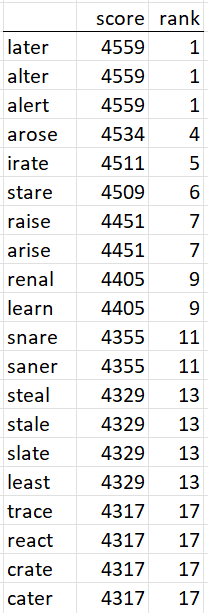
One strategy for our initial guess is to use a word that contains the most frequently used letters. “later” is such a choice. Figure 2 contains a list of initial guesses from the basic Wordle dictionary that use the most frequent letters without repeating a letter.
Figure 2 – Guesses based on frequently used letters
There are also quite a few words from the full, 12,497-word, dictionary that could be added to this list, including a few words that would rank higher than those that appear in Figure 2 (“orate”, “oater”, “roate”, “realo”).
Figure 2 includes multiple occurrences of the same letter (e.g. “e” in “geese”). Figure 3 provides a similar list where multiple occurrences of the same letter are only counted once. Thus, for example, 39.3% of the words in the dictionary contain the letter “a”.
Figure 3 – Letter frequency
Possible Patterns
Based on the rules for Wordle described in Wordle Strategy, after each guess that you make, Wordle responds by highlighting your guess with one of three colors, red, yellow, or grey. Thus, there are 243 (= 35) possible Wordle color codes for any guess. We will call this a “pattern”, which consists of a 5-letter word using the letters “G”, “Y”, or “*”. Here, “G” stands for green, “Y” stands for yellow, and “*” for grey. The 243 possible patterns are shown in Figure 4.
Figure 4 – Wordle Patterns
Reference
New York Times (2022) Wordle
https://www.nytimes.com/games/wordle/index.html
My four words with 19 of the top 20 letters (I have #21, W, instead of #20, K):
CANES
WORTH
BLIMP
FUDGY
Hey, they work for me.
Dan,
Thanks for the feedback.
Charles
How about the following?
CAKES
NORTH
BLIMP
FUDGY
Charles
If you had to pick 4 words to maximize the probability of being able to solve a word, which 4 would you pick? I ask this because I often play Octordle which is 8 wordles at the same time in 13 guesses, so you want a to get all the common letters in there in their common spots and solving one at a time doesn’t work.
My not optimal current words are
Party
Blink
Mouch
Feeds
After reading your analysis I was looking to get a ‘G’ in there and maybe remove an E.
Also if I were to keep the double E, I should try to get them in the 4th and 5th position.
Thank you!
Hi Jared,
I can see that you are trying to use all the top 20 letters without repetition. I wasn’t able to find a better solution in the 10 minutes that I devoted to the task, but perhaps the word FORGE would be useful. This would work if MUCHS were a word to replace MOUCH. In any case, perhaps you can do something with this.
Charles
John, my goal is to win the game and I usually do it in four.
My strategy is to get the vowels out and use three different words containing 15 different letters. I dislike uncommon words that are seldom used. Just a personal preference I guess.
My first word is aeons, which contains three vowels.
This gives me valuable information. If I have 0 or 1 vowel, my second word is build and the third crypt.
If I have 2 or 3 vowels, I place more emphasis on consonants. My second word is lymph and the third trick.
Quite often at this point I have determined 4 letters, sometimes 1 or 2 are green. Occasionally I get lucky and the winning word seems obvious. I then abandon the formula and go for the gold. Suppose the winning word is snare. I would then have four yellow letters after using aeons. I would then think that the word probably starts with s and ends with e. If sn, then the third letter must be a. I am missing the r!
I am always open to new ideas and would welcome and comments or suggestions you might have.
Regards,
John,
Thanks for sharing this.
Charles
Charles,
You may be happy to hear that I’ve seen the light.
For one thing always entering SLATE + IRONY was hardly more challenging or interesting than entering SLATE followed by a second guess from your list. The sole advantage of always using IRONY was that I could claim that it was something I thought of myself.
The main point , however, is that I’ve come to realize that always using the same first two guesses is a pretty poor idea. Instead the second guess has to take into account the information provided by the results of the first guess. This is well illustrated by the terminal Y in IRONY. I think that it makes good sense provided that the first guess does not reveal a terminal E (as Y is relatively common and almost always occurs in the last position). But it makes no sense at all if the first guess does reveal a terminal E, as in this case Y occurs in at most one of the remaining possible words.
I see how the probability of solving in 3 is equal to N/W, where W is the number of words remaining after the first guess and N is the number of patterns that might be returned by the second guess. The probability of winning in 3 is therefore maximized by minimizing W and maximizing N. How about using RAISE as the first guess? I’ve read that it minimizes the average value of W, and its worst case (*****) behavior is certainly significantly better than that of SLATE (W = 165 rather than W = 221).
If all one cares about is maximizing the probability of winning in 3 tries, it doesn’t matter how the W words are spread over the N patterns, but this matters a lot if one is interested in minimizing the average number of guesses to solve, or in avoiding the possibility of not solving at all. Take today (POWER) as an example. SLATE left 165 words on the table (not a great start!) but I was encouraged by the fact that DINER was going to spread these words over 63 patterns. I’d have a 0.38 probability of solving in 3, and on average I’d be left with just 2.6 words to deal with. But in the event I was left with 29 words, and they included a lot of those nasty “ryhming words” (mover, cover, rover, etc.) that can eat up guesses in a hurry. Happily I got a bit lucky and solved in 4, but I would have preferred a second guess may have produced fewer possible patterns (and hence a lower probability of solving in 3) but that also reduced the maximum number of words per pattern.
Might it be possible to produce a set of second guesses that is rather more tailored to avoiding the worst case by using a somewhat different objective function (one that both takes into account the value of increasing N and the desirability of spreading the W words as evenly as possible over the N patterns)?
Regards – John
Hi John,
It looks like our thinking about Wordle is converging.
“raise” seems to be an excellent first guess. The probability of winning within 3 tries is 55.8%, which is not far from “slate”. It is possible that the average number of tries to winning is better. I have not tried to solve this problem yet. I was starting to investigate the best moves to win within 4 tries, but I got distracted by other things before I obtained a solution.
Charles
Charles,
To say that our thinking is converging rather flatters my contribution. I think its more a case of my ignorance being overwhelmed by your insight.
I think I can now quantify what I’m getting at, and today’s WORDLE (spoiler alert) provides a good example. SLATE returned G**Y*, leaving 39 possible words. At this point your table called for me to use CHUNK as my next guess, but after looking at the letter frequency for the remaining words I chose to use FRONT instead. This left me with 5 possible words (STOOP,STOCK,STOMP,STOIC, STOOD) and a choice between using CRIMP as a test word (guaranteed solution in 4) or taking a chance on STOOP (1/5 chance of solving in 3, 3/5 chance of solving in 4, and 1/5 chance of solving in 5). As the average number of guesses was the same, I went with STOOP and solved in 4. After the fact I investigated the relative merits of CHUNK and FRONT. CHUNK produces 19 possible patterns versus 15 for FRONT and so gives both i) a higher probability of solving in 3 and ii) a lower number of words per pattern (i.e. on average, one will be left with fewer remaining words). But CHUNK might leave one with 9 remaining words (and this would have happened today) while FRONT will never leave one with more than 5. So unless there’s a test word that will distinguish between SPORT,STIFF,STOMP,STORY,STORM,STRIP,SWIFT,STOOD, and STOOP (an interesting little WORDLE problem) CHUNK does not guarantee a solution in 4, whereas FRONT probably does (I’d have to check that there are test words for all of the 6 other patterns that leave more than 2 possible words).
Can I suggest that you modify your table of second guesses so that it includes the worst case number of words remaining? It’s not something I need now that I have the means of working it out, but this information might be of interest to others.
And I would really like to see a second table that gives, for each possible pattern, the second guess that minimizes the worst case number of remaining words (with the pattern count used as a tie breaker). There may well be, for example, a guess that is even better than FRONT in this regard.
Regards – John
P.S. I don’t know how you broke ties in compiling the existing table, but I’d suggest that the worst case number of remaining words would be a good choice.
Oops – I wasn’t thinking. The average number of words left after a guess isn’t inversely proportional to the number of possible patterns. This is because patterns that correspond to a larger number of words are more probable. Using FRONT rather than CHUNK gives one both a lower average number of words (3.410 vs 3.872) and a lower worst case number of words (5 vs 9). CHUNK is better only in that it gives a somewhat higher probability of solving in 3. Elsewhere in the table DONER is much better than DINER after ****Y if one’s figure of merit is the average number of words (7.218 vs 8.152) or the worst case number of words (20 vs 29), though the lower number of patterns (56 vs 63) does mean that one has a lower probability of solving in 3.
So now we have three possible ways of evaluating possible second guesses. One can maximize the number of patterns (the probability of solving in 3), minimize the average number of words remaining, or minimize the worst case number of words remaining.
Hi John,
Regarding (1) Maximizing the number of patterns (the probability of solving in 3), (2) Minimizing the average number of words remaining, or (3) minimizing the worst case number of words. I assume that by (2), you mean the average number of tries to guessing the target word.
As a first step, I am thinking about providing the following info for any second guess:
(1) Number of patterns, (2) average number of tries to victory, and (3) worst case number of tries to victory.
Charles
Hi John,
I expect to add some more information about Wordle to the website as well as to the software to address some of the issues that you have raised. Thanks for all your comments. It has been very helpful to me.
Charles
From your WORDLE word choices, it appears you are playing in Easy mode. Hard mood requires that in subsequent words Green letters must appear in the same place it appears in previous words, and Yellow letters must appear in subsequent words but may be used in any place in the word. I would really like to see an algorithm for that mode.
If you want more of a challenge use a different word each day of the month, never repeating the same first word within the month. This approach slightly increases the importance of a good second word, especially in hard mood. I would like to see a list of the best second words.
A friend plays the same first word as me each day. We make a list of 28 to 32 words each month, using a category to restrict the words that can be selected as first words. For example, one month’s list was restricted to words appearing in the titles of the top 100 songs (according to Billboard and Official Charts as shown on Wikipedia) released in a certain year. Another month we used words appearing in Beatles lyrics.
Over 290 WORDLES I have an average solve rate of 3.75, using this method of choosing first words, with one failure to solve. My friend has an average of about 4.0 with no failures to solve. Of course, the choice of the best second word is crucial with this approach. According to an article in NYT, the average number of words to solve among those choosing to have NYT accounts (free to $1.50/month and up) and giving permission to be included, is about 3.8. They developed an algorithm for solving in the minimum number of turns. It has an average 3.4. It is called WORDLE-Bot. https://www.nytimes.com/interactive/2022/upshot/wordle-bot.html
It uses LEAST as its first word. This is based on its evaluation of which words are most likely to be a solution comparing words that have already appeared as solutions compared to its list of the most common five-letter words in English. It uses a solving method almost identical to the approach(es) described here.
Well done. And keep up the good work, perhaps using my suggestions for further analysis.
John,
1. Looks like you are making great progress with your analysis. It seems to me that coming up with guesses that minimize the average number of tries is a harder problem than guesses that maximize the probability of victory in 3 turns. As I said in an earlier response, I know how to maximize the probability of victory in 4 turns, but I haven’t had the energy to complete the implementation.
2. I have an idea about providing a partial solution to the issue of the average number of tries. I’ll look into this.
3. I’ll also look into your suggestion about modifying the table of second guesses so that it includes the worst case number of words remaining.
4. I break ties simply by choosing the alternative lowest in alphabetic order. If I solve #3, it will be easy to pick the alternative with the lowest worst case.
Charles
Charles,
I was thinking of average number of words as the expected number of words remaining after the guess. This is easily calculated as [sum Pi * Wi ] = [sum Wi^2 / W] /, where W is the total number of words remaining prior to the guess, Wi is the number of words associated with the ith pattern, and Pi is the probability of this pattern occurring (Wi/W). And the maximum number of words remaining after the guess is simply max(Wi). Working out the average and maximum number of tries required to solve is an altogether more challenging problem, and I’m not sure that this information would add all that much. Intuitively the average number of guesses will tend to follow the average number of words remaining, and the maximum number of tries required to solve is connected to the maximum possible number of words remaining.
One complication is that the number of words remaining doesn’t correlate directly to the number of guesses required. 1 word remaining does give (avg = 1, max = 1) and 2 words (avg = 1.5, max = 2), but 3 words remaining can mean (avg = 2, max = 4) or (avg =1.67, max = 2) or (avg = 2, max = 2) depending upon i) whether the information provided by guessing one of the words is enough to distinguish between the other two possibilities and ii) whether the next guess is used as a test rather than an attempt at a solution.
I’ve switched to using RAISE, in part so that I have to depend upon my own guesses rather than relying on your table. I am, however, beginning to have my doubts. It turns out that the superior first round performance of RAISE (an average of 61 words left vs 71.57 for SLATE, a worst case of 165 words left vs 221 for SLATE) is due entirely to the ***** and ****Y patterns. Knock these out and SLATE looks better. And the ***** pattern with SLATE isn’t really the weak point that it might appears too be. Guessing ROUND takers one down to an average of just 6.412 words remaining, and one is guaranteed that there will be no more than 14 words left. By comparison RAISE + MULCH (the best second guess that I’ve been able to come up with) leaves an average of 6.857 words, and up to 16 words may remain. RAISE + MULCH does give a slightly higher probability of solving in 3 (.357 vs .326) but clearly SLATE recovers to a position of near equality after two rounds. The *****Y situation is a bit more nuanced, and I continue to think that DINER is a poor second choice because both the average and maximum number of remaining words are so high (I now lean to NIDOR, which gives 58 patterns, an average of 6.62 remaining words, and a maximum of 17 remaining words), but SLATE does at least come out on top when it comes to the probability of winning in 3.
I’ve now modified my spreadsheet so that I can enter possible guess words and have it tell me i) the number of possible patterns, ii) the average number of words remaining, and iii) the maximum number of words remaining. Playing around with this allows me to avoid really bad guesses, come up with semi-optimal guesses, and test your suggested choices to see how well they stack up in terms of the average and maximum number of words remaining. It’s been interesting, and cramming as many as possible of the letters that occur most frequently in the remaining words into a guess is certainly no guarantee that one will achieve anything useful. Often tossing in a less frequent letter will magically improve things.
– John
The fact that the word GEESE has three E’s in it serves to make E more “frequent”, but does nothing to increase that a probability that a guess word with a single E in it will produce a hit. I’d be interested in knowing the fraction of Wordle words that contain an E, the fraction of words that contain an A, and so on. This approach would produce somewhat different results in that letters that are frequently doubled would become less common, and letters that are rarely doubled would become less so.
Hi John,
Good point. I have just added a new letter frequency table to the webpage (see the new Figure 3).
Charles
Thanks. This does change things a bit (e.g. C drops from being the 10th most common letter to being the 11th, and U moves up one spot). If the initial two guesses are to cover the ten most likely letters they must include all of EAROTLISUN (e.g. AROSE + UNLIT is one possibility). One plus to this strategy is that after the first two guesses the vowel situation will be known (save for the possibility of duplicates and Y). Personally I think that this is the way to go. If testing for the most common letters produces lots of hits (as might reasonably be expected) one will be left in good shape, and if there are two or less hits this is in fact also good news. Being able to eliminate all words containing common letters narrows things down a lot.
John,
It turns out that letter frequency is less important than pattern frequency. This is explained elsewhere on the website.
Charles
Ah, but where’s the fun in simply manually implementing what is essentially a computer generated solution? I’m looking for a strategy that is within my abilities.
Another objection to a letter frequency approach is that it assumes that words are randomly chosen from the list of possible words. I’m not sure that this is the case, and have a hunch that words with lots of common letters are less likely to be chosen. They’re on to me!
Hi John,
I understand. My insight was to recognize that pattern frequency was better than letter frequency. Once I understood that the rest was, as you have said, a computer-generated solution.
Charles