Objective
We show how to determine the best three guesses to maximize the chances of winning at Wordle using Excel. This will be done using Real Statistics worksheet functions. For our purposes, winning means identifying Wordle’s target word within three guesses.
In what follows, guess and guess1 are text strings representing 5-letter English words, and pattern and pattern1 are positive integer values between 1 and 243 representing a pattern (e.g. 1 represents “*****”).
Real Statistics utility functions
DictList(full): array function that returns a column array with all the words in the dictionary.
When full = FALSE (default), the basic dictionary containing 2,315 words is used, while when full = TRUE, the full dictionary containing 12,947 words is used.
The worksheet in Figure 1 contains the output from the formula =DictList(). Only the first 10 rows of the output are displayed. See Figure 1 of Wordle Winning Strategy for a complete list of dictionary words.
Figure 1 – DictList()
The formula =DictList(TRUE) returns a longer column array beginning with the word “aahed” and ending with the word “zymic”.
PatternId(spattern) = the pattern identification number corresponding to the specified pattern, spattern, expressed as text with 5 characters.
The patterns can be listed in the order “*****”, “****Y”, “****G”, “***Y*”, etc., as displayed in Figure 3 of Letter Frequency and Patterns. These correspond to the pattern id numbers 1, 2, 3, 4, etc. Thus, PatternId(“***Y*”) = 4. Similarly, PatternId(“***GY”) = 8.
SPattern(pattern) = the 5-letter text string for the pattern with the specified pattern identification number pattern.
This function is the inverse of PatternId. E.g. PatternId(“G*GY*”) = 184 and SPattern(184) = “G*GY*”).
Real Statistics function for the first guess
PatternCount(guess) = # of patterns for which some target has this pattern for the specified guess.
You can obtain the results in Figure 2 of Winning Wordle in Two Tries by using this function. E.g. the count of 150 for “trace” can be obtained via the formula =PatternCount(“trace”).
Best second guess function
BestGuess2(guess1, pattern1, ttype): returns a 4 × 1 array containing the following items where guess1 is the first guess and pattern1 is the pattern returned for this guess
- the second guess with the highest number of non-zero patterns, but if there is more than one of these, then the guess whose largest number of targets for any pattern is the lowest
- the number of non-zero patterns for this guess
- the number of other guesses with the same number of non-zero patterns
- the largest number of possible targets for this guess for any pattern.
When ttype = 0 (default), the second guess can be any word in the basic dictionary of 2,315 words. When ttype = -1, the second guess is restricted to words from the basic dictionary that could be targets of guess1. When ttype = 1, the second guess can be any word from the full dictionary consisting of 12,947 words.
Note that the processing time when ttype = 1 is a little slower than when ttype = 0 or -1.
Examples
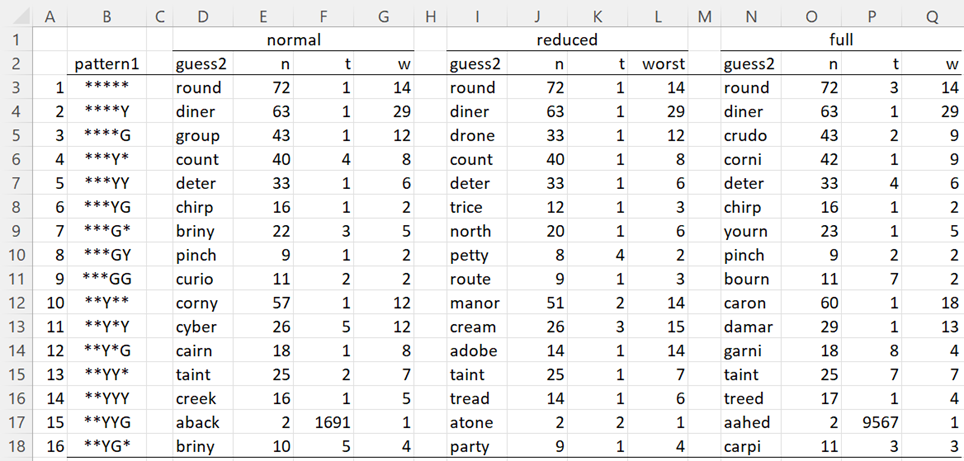
Range D3:G3 of Figure 2 shows the output from the formula =BestGuess2(“slate”,A3), while I1:L1 contains the results of =BestGuess2(“slate”,A3,-1), and N3:Q3 contains the results of =BestGuess2(“slate”,A3,1).
Figure 2 – BestGuess2
These results are similar to those shown in Figure 3 of Best First Two Guesses for the best second guesses from the 2,315-word dictionary (normal) and best restricted second guesses (reduced). In addition, the best second guesses from the 12,947-word dictionary (full) are also displayed (similar to Figure 1 from Best Guesses from the Full Dictionary).
Fine-tuning the results
Note that there are 3 differences between the items in Figure 2 and those displayed in Figure 3 of Best First Two Guesses. The BestGuess2 function finds the guess with the highest target count value. If there is a tie, then it uses the worst count to break the tie. If there still is a tie, then it uses the first such choice in alphabetical order.
This is why “aback” is listed as the best second guess for pattern 16 in Figure 2, but “atone” is listed as the best second guess in Figure 3 of Best First Two Guesses. Here “atone” is a better choice since it is a restricted guess and so has the possibility of a win in two tries, whereas “aback” can result in a win in two tries.
“count” is listed as the best second guess for pattern 4 in Figure 2, but “round” is listed as the best second guess in Figure 3 of Best First Two Guesses. This is because the probability of winning within 4 tries is 70.9% when “round” is the second guess, while the probability of winning within 4 tries for “count” is 67.4%. This can be discovered using the WordleProb2 function, described below.
The situation for pattern 16 is similar between “briny” and “harpy”. They have the same probability of success in 3 tries, but “harpy” has a higher probability of a win on the 4th try (86.7% vs. 80%).
Finally, note that for pattern 1, BestGuess2 indicates that the best second guess from the full dictionary is “round”, but actually “drony” offers a higher probability of a win on the 4th try (51.1% vs. 48.9%).
Probability function for the second guess
WordleProb2(guess1, pattern1, guess, lab); returns a column array containing the following entries where guess1/pattern1 represents the first guess and guess represents the second guess: # of non-zero patterns, # of compatible targets, probability of winning within 2, 3, 4, 5, and 6 tries, worst case pattern, and # of targets for that pattern. If lab = TRUE then a column is appended to the output with labels (default is FALSE).
Here, we assume that the response (i.e. pattern) by Wordle to the third (or later) guess is not used. In fact, you may be able to improve the probability of winning within 4 tries returned by this function by using the additional pattern information.
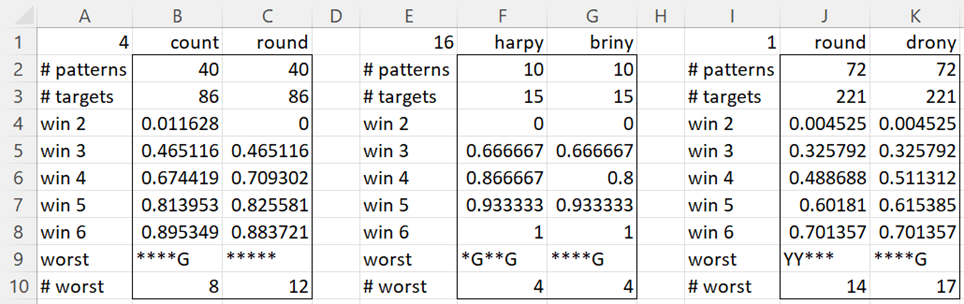
We can use the WordleProb2 function to compare two potential second guesses, especially when they have the same probability of a win within 3 tries (i.e. the same number of non-zero patterns). The last three comparisons described for the BestGuess2 functions are shown in Figure 3. In each case, the probability of a win within 3 tries is the same, but the probability of a win within 4 tries is not the same.
Figure 3 – WordleProb2
Here, range A2:B10 contains the array formula =WordleProb2(“slate”,A1,B1,TRUE) and C2:C10 contains the array formula =WordleProb2(“slate”,A1,C1). The formulas for the other 4 guesses are similar.
Refinements
The rule of thumb given in Refinements to Best Second Guess is that usually if the number of non-zero patterns is the same, pick the second guess with the smaller worst-case number of targets (for any non-zero pattern). This guideline is violated in the first and third examples of Figure 3. Note too that while “round” offers better odds for victory in 3, 4, or 5 tries, it is worse for 2 or 6 tries.
Finally, note that WordleProb2 sometimes gives erroneous results for a win within 2 tries for guesses from the full dictionary, such as for “drony”. This is because although “drony” is compatible with pattern 1 for “slate”, since it is not in the 2,315-word dictionary, it can’t be a target, and so the probability of a win within 2 tries is zero. Note that this doesn’t impact the other values in the output.
Second guess targets
Targets(guess, pattern): returns a column array with all the target words that are compatible with guess/pattern
TargetCount(guess, pattern) = the number of target words that are compatible with guess/pattern
As we observe in Figure 1 of Refinements to Best Second Guess, there are 10 target words that are compatible with “slate”/”***GY” (pattern id = 8). Thus, TargetCount(“slate”,8) = 10 and Targets(“slate”,8) returns a column array with the 10 target words in Figure 1 of Refinements to Best Second Guess.
Other Real Statistics functions for the second guess
Pattern2Counts(guess1, pattern1, guess): returns a column array with 243 rows, one for each pattern, with the count of targets that are compatible with guess1/pattern1 for the first guess and compatible with guess/pattern for the second guess.
This function provides the details used to determine the results provided by WordleProb2. E.g. after “slate”/”*YY**” (pattern id 37) suppose we choose “molar” as our second guess. As noted in Refinements to Best Second Guess, among the 26 non-zero patterns for “molar”, 16 of them have only 1 potential target, 4 have 2 potential targets, 3 have 3 potential targets, 1 has 5 potential targets, 1 has 8 potential targets, and 1 has 12 potential targets. We see this by using the Pattern2Counts function.
In particular, we place the array formula =Pattern2Count(“slate”,37,”molar”) in range C1:C243. Figure 4 shows the result where we only display the 26 entries in the output that are non-zero.
Figure 4 – Pattern2Counts
Guesses2(guess1, pattern1, npatterns, ttype); returns a column array containing all the words in the dictionary that are compatible with guess1/pattern1 and have npatterns many non-zero patterns. ttype is as for BestGuess2.
We see in Figure 2 that after “slate”/”**Y*Y” (pattern id = 11), there are five words in the 2,315-word dictionary that produce 28 non-zero patterns as a second guess. We can use the formula =Guesses2(“slate”,11,28) to produce a column array with these five words, namely “bread”, “broad”, “cream”, “cyber”, and “debar”.
Finally, note that these words are equally likely to yield a win within 3 tries. We can use WordleProb2 to determine which of these is better for victory within 4 tries if the target is not yet identified after 3 tries.
Real Statistics function for the third guess
Guesses3(guess1, pattern1, guess2, order): returns an array with all possible third guesses for each possible second-guess pattern after an initial guess of guess1 to which Wordle responds with pattern1, followed by a second guess of guess2. Each entry in the output contains both the second-guess pattern and the corresponding third guess.
Three formats are available. When order = 0, the output is sorted based on the third guess. When order = 1 (default), the output is sorted based on the second-guess pattern. Finally, when order = -1, the output is sorted based on the second-guess pattern, but only one row per pattern is output along with the number of possible guesses for that pattern.
Best third guess example
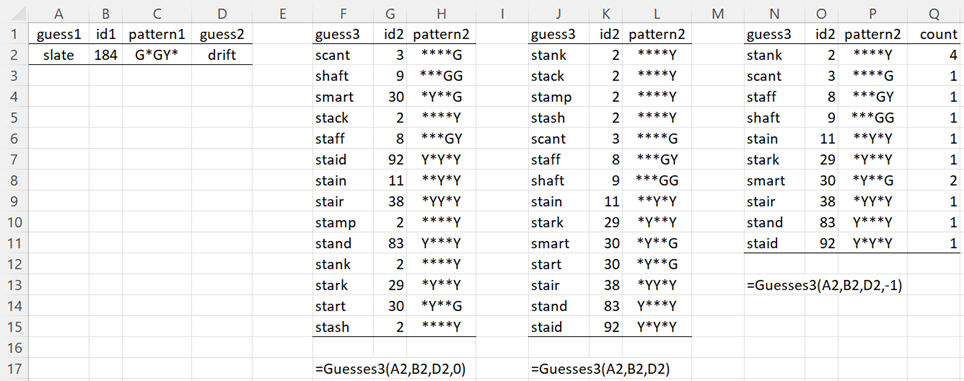
We now give an example of how to use Guesses3. Suppose that your first guess is “slate” and Wordle returns the pattern “G*GY*”. You now choose “drift” as your second guess (which is close to being the best choice). Your third guess now depends on the pattern that Wordle returns to your second guess of “drift”. This is shown in Figure 5.
Figure 5 – Guesses3 example
The 14 targets that are compatible with “slate”/”G*GY*” are shown in column F. For each of these targets, column G (or H) displays the pattern that Wordle returns after your second guess of “drift” (cell D2). The values in range F2:H15 are returned using the formula =Guess3(A2,B2,D2,0), i.e. the version with order = 0.
A more useful way of looking at the same information is shown in range J2:L15, which is obtained using the same Guesses3 formula but with order = 1. This time the information is sorted by pattern2. We see that if Wordle returns the pattern “****Y” after your second guess, then your best third guess is “stank” (although “stack”, “stamp”, or “stash” are equally as good). If, instead, Wordle returns the pattern “**Y*Y”, then your best third guess is “stark”.
Range N2:Q11 contains the same information as range J2:L15 in a more compact form. This is obtained using the same Guesses3 formula with order = -1. This time, each of the 10 second guess patterns is listed only once with the number of replications shown in column Q. Note that 10 is the same value shown in cell F6 of Figure 2.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
New York Times (2022) Wordle
https://www.nytimes.com/games/wordle/
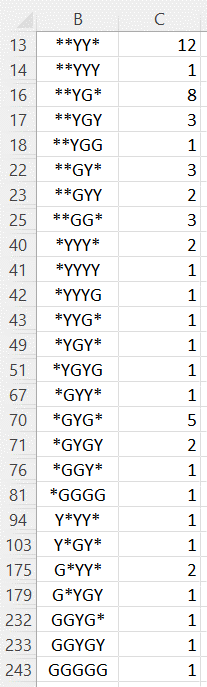
Charles,
I was wondering how you obtained the 2315 word list. Is this public information?
According to this article (which came out today), they added about 30 words to the dictionary. The article is about what the NYT will do when they run out of words.
https://www.techradar.com/computing/websites-apps/wordle-will-eventually-run-out-of-words-here-s-what-the-nyt-could-do-next
Jonathan
This post includes a video with the lady at NYT who controls the word list.
https://www.eurogamer.net/wordle-is-running-out-of-words
Hi Jonathan,
I believe that the 2315 number was public information at the time I wrote this webpage.
Charles
I forgot to add.
4) Since Wordle never repeats an answer, how does that factor into your analysis? Do you have a version of this analysis that removes the words that have already been the answer?
Hello Jonathan,
You have made an important observation. I have not taken into account previous target words. I have not created a version that takes this into account.
Charles
In case you want to do that, the web site I use to check past answers is https://www.fiveforks.com/wordle/
It lists them in alphabetical and chronological order.
Charles,
This is excellent analysis! Thank you for this resource.
I have some questions.
1) Can you explain in more detail why “TRACE” is a better start word than “ROATE”? I found that analysis on another website. They say it gives you the best “average”.
2) Have you done any analysis on the success of getting the first letter “green” vs. the other 4 positions. I go on the theory that matching the first letter tells you more about the word than the other 4. I would rank the last letter (5th position) as second. I would rather get those 2 letters green than the other 3.
3) What is the relative value of getting a “green” letter vs. a “yellow” letter? Is getting one “green” better than getting 2 yellows?
Hello Jonathan,
1) I found that TRACE was the best choice for winning in one or two guesses. I did this by looking at every possible target word and seeing what the probability of winning in one or two guesses for each. TRACE came out on top. I found that SLATE was best for winning in 1, 2, or 3 tries. I suspected that TRACE was best for best average, but someone else calculated that TRACE was best.
2) I haven’t done this analysis, but it would be dependent on the following criteria: (1) what is your first guess? Is it TRACE?, (2) what is success? Is it lowest average number of guesses? It may be that for the above, “best” was usually defined as best average assuming no more than 5 guesses were ever required.
3) See remarks for (2).
Charles