Objective
Our goal is to determine a strategy for determining the target word in the least number of guesses averaged over all possible target words. E.g. suppose that you have a strategy that guesses 1 of the target words in 1 turn, 100 of the target words in 2 turns, 400 of the target words in 3 turns, 1200 of the target words in 4 turns, 100 of the target words in 5 turns, and 4 of the target words in 6 turns.
Since 1+110+600+1500+100+4 = 2315, we have accounted for the possible target words. The expected number of turns for this strategy is therefore a weighted sum divided by the number of targets, namely
We need to insist that our strategy guarantees that the target word will always be guessed within 6 tries (the maximum number of tries allowed). In fact, as we will see, the minimum expected number can actually be achieved in 5 or fewer guesses.
Strategies to minimize the expected number of guesses
We present three versions of the strategy to minimize the expected number of guesses starting with an initial guess of “trace”.
- For any pattern after a first guess of “trace”, minimize the number of targets guessed in 5 tries, and if there is more than one such approach, then pick the one that also minimizes the number of targets guessed in 4 tries.
- For any pattern after a first guess of “trace”, maximize the number of targets guessed in 2 tries, and if there is more than one such approach, then pick the one that also maximizes the number of targets guessed in 3 tries.
- For any pattern after a first guess of “trace”, maximize the number of targets guessed in 3 or fewer tries.
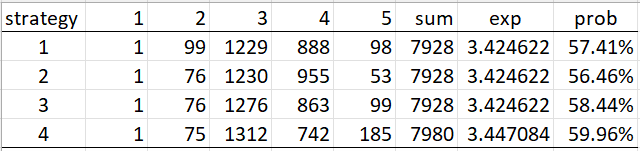
All three of these strategies achieve an expectation of 3.425; i.e. on average, you will win Wordle in 3.425 guesses. Furthermore, you will never need more than 5 guesses.
Click here to see a summary of strategies 1 and 2.
For each pattern after an initial guess of “trace”, this webpage displays the number of targets compatible with that pattern, along with the best second guess for strategies 1 and 2 and the number of targets identified in 1, 2, 3, 4, or 5 tries (assuming that you make the appropriate 3rd, 4th and 5th guesses). The weighted sum and expectation for each pattern are also shown. Similar information for strategy #3 is available below.
Winning in 3 tries while minimizing expectation
In Winning Wordle in Three Tries, we explain that the probability of guessing the target word within 3 tries starting with “trace” is 59.9568%. It is possible that this might lead to situations in which some target words are found within 3 tries, but other targets might not be found within the allotted maximum of 6 tries.
We seek a strategy that achieves the 59.9568% probability for guessing the target within 3 tries, but which never requires more than 5 guesses, well within the maximum allowed under the rules for Wordle. We also want to find such an approach that requires the minimum expected number of guesses. This is strategy #4.
- Minimize the expected number of guesses to identify the target word (within 5 tries) while maximizing the probability of guessing the target word within 3 tries.
The cost for this strategy is that the expected number of guesses is slightly higher than the minimum expectation described above.
In fact, the expected number of guesses for strategy #4 is 3.447, only a little higher than for strategy #3, although strategy #4 has the advantage that the probability of guessing the target within 3 tries is better than for strategy #3 (59.9568% vs. 58.4449%).
Click here to see a summary of strategies 3 and 4.
For each pattern after an initial guess of “trace”, this webpage displays the number of targets compatible with that pattern, along with the best second guess for strategies 3 and 4 and the number of targets identified in 1, 2, 3, 4, or 5 tries (assuming that you make the appropriate 3rd, 4th and 5th guesses). The weighted sum and expectation for each pattern are also shown.
Summary
Figure 1 displays a summary of the results for all four strategies. The column labeled prob shows the probability of winning in 3 guesses or less for each strategy.
Figure 1 – Summary
Developers of the strategies
These 4 strategies were developed via a collaboration with John Bryant. A few months ago, John sent a comment to the Real Statistics website with some interesting ideas about how to “solve” Wordle. Since then, we have combined forces to achieve the results described above.
Note that the strategies presented above attempt to minimize the expected number of guesses. We have gone through a number of potential approaches and have found these to be the best. It is, however, possible that there may be refinements that produce better results (i.e. strategies with a lower expectation), although we believe that the strategies described above are close to the optimum. We welcome any suggestions.
References
New York Times (2022) Wordle
https://www.nytimes.com/games/wordle/index.html
Scholtes, G. (2022) Wordle dictionary. Github
https://gist.github.com/scholtes/94f3c0303ba6a7768b47583aff36654d
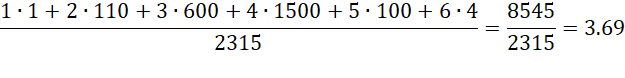
Hi Charles,
I presume you are aware of the MIT study and associated paper
https://auction-upload-files.s3.amazonaws.com/Wordle_Paper_Final.pdf
In this they claim an average of 3.421 guesses to solve Wordle, which is clearly just a fraction below yours, although I believe it is also considerably more complex.
This is not to denigrate your work in any way, as I think your approach is far more useful to normal humans (vs computers), and therefore simply highlights how close you may be to the absolute minimum.
I will note also that their system only finds words in the original 2315 Wordle target list (although it utilizes the full dictionary for guesses), which I consider a poor constraint now that the editor is free to choose other targets (and has done so on several recent occasions – GUANO and SNUFU, I believe).
I guess the problem of leaving the Wordle list behind is that you don’t have a consistent reference list against which to measure your potential success rate unless you expand to the entire guess list, which clearly contains some very unlikely targets.
If you are interested in collaborating on the development of an extended list of potential Wordle targets that would be a culled list of the allowable guesses, please let me know, as I started on such a project but found it a little overwhelming!
But having looked at both approaches and learnt a lot in the process, I arrived at the conclusion that SALET was likely the best starter word for an extended word list, as it seemed to give rise to the greatest number of patterns. If you have any basis to refute that proposal under the assumption we don’t know what target words the Wordle editor could now choose, I would be very interested in seeing it.
Regards, Ian Bradford.
Hi Ian,
How has your development of an extended list of potential Wordle targets going?
Are there any new developments regarding Wordle?
Charles