Objective
As stated at Wordle Winning Strategy, our goal is to describe a strategy that maximizes the chances that you will guess the target word within three tries. We will restrict ourselves on this webpage to the case where the first two guesses are from the basic Wordle dictionary of 2,315 words. How to improve on these selections when you can make guesses from the full dictionary of 12,497 words is described in Second Guess from Full Dictionary.
It turns out that “slate” is the best initial guess for achieving this objective, although “trace” also has some advantages. We say more about this at Winning in Three Tries. On this webpage, we explain how to make the best second guess depending on Wordle’s response to your first guess.
Example using “beach” as the second guess
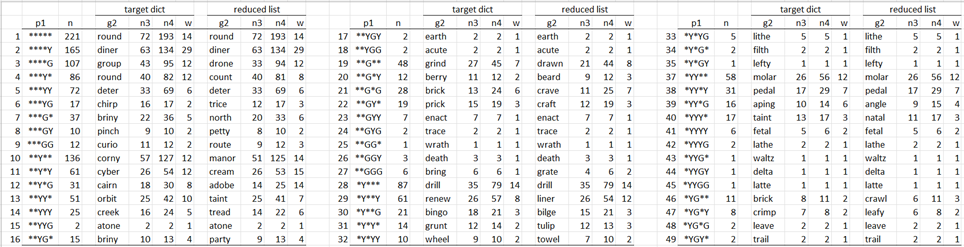
Let’s suppose that Wordle responds to the initial guess of “slate” with the pattern “**G*Y”. There are 12 targets that would produce this pattern, namely
Figure 1 – Targets that match “**G*Y”
If we now select “beach” as our second guess, then as we see in Figure 1, there are 5 possible patterns that can result, namely “*GG**” containing 4 targets (“ready”, “rearm”, “weary”, “yearn”), “*GG*Y” containing 3 targets (“heavy”, “heard”, “heavy”), “*GGGG” containing 2 targets (“peach”, “reach”), “GGG**” containing 2 targets (“beady”, “beard”), and “GGGGG” containing 1 target (“beach”).
We see that “beach” partitions the words in Figure 1 into 5 disjoint buckets. In this case, if “beach” is chosen as the second guess, then Wordle will return one of these 5 patterns. If it returns the “*GG**” pattern, then you can choose any one of the 4 qualifying targets as your third guess, giving you a .25 probability of guessing the target correctly within three tries (our goal). If instead, Wordle returns “*GG*Y”, then you will have a 1 in 3 chance of guessing the target in three tries.
The probability in this case of a win, i.e. guessing the target word within 3 tries, is therefore
We see that the more partitions there are, the fewer valid choices there are for the third guess, thereby increasing our probability of guessing correctly.
Example using “beard” as the second guess
From Figure 1, we see that a better choice is “beard”, which produces 9 non-zero patterns. In fact, if we restrict our second guess to those words that are consistent with the first guess and the first-guess pattern, then “beard” would be an optimum choice as a second guess (although “heady” or “heard” could be used instead since they also produce 9 such patterns).
Using “beard” as a second guess partitions the 12 words in Figure 1 into 9 disjoint buckets, 7 of which contain only one word. If Wordle returns one of these 7 patterns, then you can guess the target word with 100% probability. If, instead, Wordle returns “*GG**” then there are two possible targets “peach” and “heavy”; selecting either one of these as your third guess gives you a 50% chance of success. Finally, if Wordle returns the pattern “*GGG*”, then there are three possible targets “heard”, “weary”, and “yearn”; selecting any one of these as your third guess now gives you a 1/3 chance of success. Overall, the probability of a win after choosing “beard” as the second guess is 9/12 = .75.
Example using “berry” as the second guess
If we don’t need to restrict our second guess to those words that are consistent with the first guess and the first-guess pattern, then it turns out that “berry” is an optimum second guess since it produces 11 non-zero patterns, better than “beard” with only 9 non-zero patterns. While “berry” can’t result in a win in only two tries, it improves your odds of winning in three tries. The partition of the target words from Figure 1 is shown in Figure 2.
Figure 2 – Third guesses after “berry” as the second guess
We see that after choosing “berry” as our second guess, Wordle can return any one of 11 different patterns. Each of these patterns corresponds to only one of the 12 possible target words, with one exception, namely “*G**G” which corresponds to targets “heady” and “heavy”. For any of the 10 patterns with only one word, all you need to do is choose this word to win within three tries. If, instead, Wordle returns the pattern “*G**G”, then you can choose “heady” or “heavy” as your third guess and have a 50-50 chance of winning in three tries. Overall, the probability of a win after choosing “berry” as the second guess is 11/12.
Best second guess after “slate”
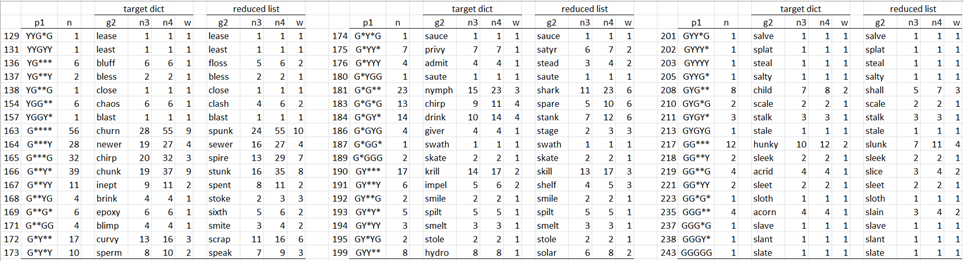
Using the same approach for all the other patterns, after an initial guess of “slate”, Figure 3 displays the best second guess for each of the 147 non-zero patterns.
Figure 3 – Best second guess after “slate”
Patterns such as “GG*GG” are not shown in Figure 3 since none of the 2,315 possible targets produce this pattern after an initial guess of “slate”. For each of the other 147 patterns, Figure 3 shows the number of targets that match that pattern (p1) after an initial guess of “slate”, the best second guess (g2) along with the number of non-zero second-guess patterns for that guess (n3). The figure shows the best second guesses from the basic dictionary (target dict) as well as the best restricted second guesses (reduced list).
Refinements to the Best Second Guess
Our goal for the second guess is to optimize the chances of winning within 3 tries. It turns out that often there is more than one such choice. In this case, it can be beneficial to choose the option that maximizes the chances of winning in 4 tries if we fail to win within 3 tries. If there is still more than one choice, we choose the one with the smallest worst-case pattern.
In fact, the guesses shown in Figure 3 reflect this refinement of our strategy (via the n4 and w columns).
Click here for more information about this refinement to our strategy for choosing the best second guess.
Download Table
Click here to download the Excel workbook with the table in Figure 3.
Reference
New York Times (2022) Wordle
https://www.nytimes.com/games/wordle/index.html
I think you missed an entry in your table. Let’s say the word is SEPAL. Guessing SLATE gets you GYY*Y, which you don’t have. You have GYY*G=SALVE. I tried SALVO, getting GYY**, immediately leading to SEPAL.
Hi Bill,
When I wrote this webpage, Wordle limited the target word to a list of 2,315 words. This list did not include SEPAL, which is why it wasn’t included. Do you know whether Wordle has now expanded the list of target words to include SEPAL?
Charles
Hello Charles.
Thank you for this wonderful analysis.
Can you please elaborate more on the N3, N4, and W columns of the table?
And what is the “target” vs. “reduced list” dictionary?
Thank you.
Hello John-Thomas,
Glad that you found the analysis useful.
Let’s specifically look at the 20th entry in Figure 3.
1. Here, we assume that Wordle responds with no matches (**G*Y) to the first guess of SLATE. This means that the third letter of the target word is A and E is a letter in the target word but not in the 5th position. BEARD is such a word (A in the 3rd position and E in the 2nd position). This what I am referring to as being in the “reduced list”. BERRY is not such a word since it doesn’t have an A in the 3rd position (although it does have an E in the 2nd position). BERRY is, however, in the basic dictionary since it can be used by Wordle as a target word (maybe not in the specific game that you are playing, but in some other game). i.e. it is in the dictionary containing 2,315 words.
2. I will respond to your comment about N3, N4, and W shortly.
Charles
Hello John-Thomas,
The following is the answer to your first question. I addressed your second question in another response.
N3 and N4: E.g. of the 221 target words that result in the ***** pattern after an initial guess of SLATE and second guess of ROUND, 72 can be guessed within 3 tries using the optimum strategy and 193 can be guessed within 4 tries
W: worst case. See the following webpage for an explanation:
https://real-statistics.com/wordle-strategy/real-statistics-wordle-support/
Charles
Can you analyze arise as first guess and touch as second? I’ve had much success as it hits all vowels but y and most blends. I’ve been using slate and round in practice and am not yielding as much success
Hello,
1. I also like “arise”, and, as you have said, it has a number of advantages. How it compares to other first guesses depends on yur objective. On this webpage, I am focusing on winning in one or two guesses. As stated at https://real-statistics.com/wordle-strategy/winning-wordle-in-two-tries/ “trace” as the first guess offers the best chance of achieving this goal with a probability of 6.48% (150 patterns). “arise” has 123 patterns, and so a probability of 5.31% of winning in one or two guesses. The situation will be different if you have a different goal (such as lowest expected number of guesses).
2. What to make as your second guess after “arise” really depends on what pattern Wordle returns after this first guess (as well as what is your objective). E.g. if your goal is to win within 3 guesses, then if Wordle returns no matches (“*****” pattern) after “arise”, then “mulch” is a little better choice than “touch”. This is also true if your goal is to win within 4 guesses.
3. If instead Wordle returns the pattern “****G” after “arise” then “could” gives a better probability of winning within 3 (or 4) guesses than “touch”.
Charles
Charles,
Thank you very much for adding the worst case information to your table.
The fact that DINER after ****Y can leave one with up to 29 words on the table really stands out. In comparing this to the other cases, allowance does have to be made for the fact that one is starting with 165 possible words, but it still compares badly with ROUND after ***** (which reduces 221 words to at most 18) and CORNY after **Y** (which reduces 136 words to at most 12).
I think that the exceptionally high value is due to the fact that the words involved include a lot of xxxER words that don’t share a lot of common consonants. I’ve been playing around with coming up with good second guesses after RAISE and TRACE, and the same group of words creates problems with these two words as well. In the case of TRACE and *Y***Y, I’ve been unable to come up with any second guess that produces more patterns (34) than PINES, and it can leave up to 33 words on the table.
At one point I thought that high worst case values were a serious problem, and as I’ve previously mentioned I took to using NIDOR instead of DINER. NIDOR produces rather less patterns (58 rather than 63) but seemed very appealing in that leaves one with no more than 17 possible words.
Since then I’ve examined DINER vs NIDOR in rather more detail, and have come to the conclusion that on most measures DINER is in fact the better choice. NIDOR does a slightly better job of dealing with the 32 words ending in ER, UR, or OR (and that don’t contain any of SLATDIN), but the difference isn’t very dramatic (an average of 4.438 vs 4.531 guesses to solve), and as DINER spreads the remaining 133 words over 61 rather than 55 patterns I’ve no doubt that on balance DINER is superior. The only possible reason I can think of now for choosing NIDOR over DINER is that it allows one to guarantee solution within 5 guesses (albeit at the cost of an increased average number of guesses).
In general I’ve come to realize the wisdom of your insight: the number of possible patterns is the key measure of the quality of a guess, and in practice the worst case value is seldom of any significance. In part this is because a high worst case value cuts both ways. One may end up in a somewhat awkward situation, but as there are fewer words to spread around the remaining patterns one has a better chance of winding up with just one or two remaining words. And in practice there is often a way out. If one is unfortunate enough to wind up with 29 remaining words after using DINER, one can use WHOMP as one’s third guess and be assured that this will reduce things to no more than 8 words (and if one is prepared to accept fewer possible patterns, WOMBY or ROCKY will leave one with no more than 7 words). This is very comparable to where NIDOR will leave one (in the worst case) after three guesses. Basically the O in WHOMP achieves the same separation of words that the O in NIDOR does, and as it costs essentially nothing because one needs a vowel in any case, DINER is able to largely catch up.
To date I’ve only come across one instance in which it makes sense to accept a reduced number of patterns in the interest of having a lower worst case. After TRACE and *Y***Y,
SILEN (33 patterns, worst case 28) is better on all measures than PINES (34 patterns, worst case 33), and even SOLID (just 28 patterns, but worst case only 21) gives the same average number of guesses as PINES. SOLID does give one a lower chances of solving in 3, but then it also eliminates the possibility of needing 6 guesses . Basically just what one might expect of a “conservative” guess. As this is all the result of playing around “by hand” (albeit with the assistance of what has become a pretty elaborate spreadsheet), it does have to be said that the analysis may be slightly flawed.
Thank you very much for having put together this very interesting and insightful site.
Regards – John
P.S. I’d be very interested in knowing what the best guess is after TRACE and *Y**Y. I can’t help but think that there has to be something much better than PINES.
Hi John,
Thanks for sharing your insights and for asking your question about the best guess after TRACE and *Y**Y. This got me thinking in much greater detail about these sorts of questions. I then spent several hours on the detailed analysis of four second-guess options: SOLID, SINEW, PINES, and DINES.
In what follows I will assume that the prime goal is to win within 3 tries. If you don’t win within 3 tries, you will select the guess that maximizes your probability of winning in 4 tries. Failing this you will try to maximize your odds of winning in 5 tries, and failing this you will try to maximize your odds of at least winning in 6 tries. Here is my analysis (hoping that I haven’t made a calculation error).
Your optimum strategy for winning within 3 tries is to select SINEW, PINES, DINES, or SEWEN as your second guess. These have a 34/113 probability of success. As you have mentioned, the probability for SOLID is lower, at 28/113.
For the probability of winning within 4 tries, at least among the four options considered, SOLID is best at 85/113. PINES and DINES are slightly lower at 81/113. SINEW is 78/113.
The order is similar for winning within 5 tries with SOLID at 109/113, DINES at 107/113, PINES at 106/113, and SINEW at 102/113.
Finally, the probability of winning within 6 tries is 112/113 for SINEW and PINES, but 111/113 for SOLID and DINES.
There is something to be said for each of the four options. The expected values for SOLID, PINES and DINES are approximately the same at 4.04 tries (assuming not winning in 6 tries counts as a win in 7 tries). The expected value for SINEW is 4.10 tries.
I am going to try to automate this analysis so that I can give better guidance on the website.
Charles
Charles,
My detailed analysis of PINES, SILEN, and SOLID gave the following results:
PINES (3= 31, 4=54, 5=26, 6=2, average guesses to solve = 3.99115)
SILEN (3 = 31, 4= 53, 5 = 29, 6=0, average guesses to solve = 3.982301)
SOLID (3 = 27, 4 = 60, 5 = 26, 6 = 0, average guesses to solve = 3.99115)
In all three cases, one should never lose altogether.
These results differ from yours because I’m working with different assumptions. Basically my goal is to minimize the average number of guesses while trying to solve within 5 guesses as often as possible. In the case of PINES, I have the probability of solving in 3 guesses at 31/113 rather than 34/113 (as one might expect given 34 patterns) because in three cases my objectives require choosing a third guess that cannot be correct. I think that WHOMP is the best 3rd guess after ***G*, that VALID is the best third guess after *G*G*, and that FILED is the best third guess after xGGGx. Similarly SILEN “loses” two patterns, so reducing the probability of solving in 3 to 31/113, and SOLID loses one pattern, giving a probability of solving in 3 of 27/113.
With regards to the probability of solving within 4 guesses, I have PINES at 85/113, SILEN at 84/113, and SOLID at 87/113.
And for solving within five guesses I have PINES at 111/113, and SILEN and SOLID both at 1.0 (i.e. solution within 5 guesses is guaranteed).
If there was a way of sending you a .pdf I’d be delighted to send you my analyses.
I’m tickled that I was able to land upon a word (PINES) that gives the maximum possible number of patterns (and I also came across SINEW). I had assumed that an exhaustive search would land upon something that gave more patterns (and possibly a lot more). Those ***ER words are a problem. Compare the *Y**Y and Y**** cases (after TRACE). Both involve 113 words, but in one case one can’t do better than 34 patterns (with a very high worst case), while in the other just a few minutes looking at the letter frequencies for the remaining words led me to HOIST (45 patterns with a worst case of just 9 words).
Regards – John
P.S. I’ll be commenting on your “Refinements to Best Wordle Second Guesses” when I’ve another moment. I think that we’re a way apart here……
Correction: My chosen third guess after PINES and ***G* is WOULD (and not WHOMP, which is my choice after SOLID and *G***). WOULD gives 18 patterns and a worst case of 8. In the worst case (*G***), the 8 words remaining can be dealt with by guessing RHYME. This leaves one with a 6/8 chance of solving in 5 and a 2/8 chance of solving in 6. If one limits oneself to using words that may be correct, the best third guess after PINES and ***G* is REVEL. It gives 15 patterns and a worst case of 10. I haven’t tried seeing whether the worst case can de dealt with, but strongly suspect that if one insists on sticking with possibly correct guesses there is no strategy that guarantees a solution with six tries.
John,
I was writing a response to your comment when I lost the connection and the information that I had written.
I will rewrite the response tomorrow. Stay tuned. I have details about using REVEL as a third guess.
Charles
Hi John,
1. If you guess WOULD after ***G*, then you have zero chance of winning in 3 tries. You have 18 patterns and 33 possible targets. Of the 18 patterns, 12 have only 1 target, and so for these 12 targets, you will win in 4 tries. 3 patterns will have 2 targets, and so for 3 of these targets you win in 4 tries and for 3 you win in 5 tries. 1 pattern will have 3 targets; it turns out that as long as you choose REFER or FEVER as your next guess, for 1 of these targets you will win in 4 tries and for 2 of these targets you will win in 5 tries. 1 pattern will have 4 targets; as long as you choose LEVER, REBEL, or REVEL, for 1 of these targets you will win in 4 tries and for 3 of these targets you will win in 5 tries.
Finally, 1 pattern will have 8 targets (the worst case). If you choose RHYME then you have no chance of winning in 4 tries, and, as you have stated, for 6 of the targets you will win in 5 tries and for 2 you will win in 6 tries.
Thus, for 17 of the 33 targets, you will win in 4 tries, for 14 you win in 5 tries, and for 2 you win in 6 tries. The expectation is therefore 150/33 = 4.54545.
2. If you guess REVEL after ***G*, then you have 15 patterns and 33 possible targets. Of the 15 patterns, 9 have only 1 target, and so for 8 of these targets, you will win in 4 tries and for the other (namely REVEL) you will win in 3 tries. 3 patterns have 2 targets, and so for 3 of these targets you win in 4 tries and for 3 you win in 5 tries. 2 patterns (Y**GY and G**G*) have 4 targets; it turns out that in each case, as long as you choose one of the 4 targets as your next guess, for 1 of these targets you will win in 4 tries, for 2 of these targets you will win in 5 tries and for 1 you will win in 6 tries.
Finally, 1 pattern will have 10 targets (the worst case). If you choose MOWER as your 4th guess then you have 3 patterns with 1 target (1 target wins in 4 tries, 2 win in 5 tries), 2 with 2 targets (2 targets win in 5 tries, 2 win in 6 tries), and 1 pattern with 3 targets (1 wins in 5 tries, 1 in 6 tries, and 1 in 7 tries).
Thus, for 1 of the 33 targets, you will in 3 tries, for 14 you win in 4 tries, for 12 you win in 5 tries, for 5 you win in 6 tries, and for 1 you win in 7 tries. The expectation is therefore 156/33 = 4.72727.
Yes, you can’t guarantee a win within 6 tries.
Charles
Hi John,
1. Thanks for sharing your analysis. I am impressed. Whereas, I have been trying to pick the guess that maximizes the number of patterns, are you trying to reduce the worst-case pattern (i.e. the pattern with the fewest number of targets)?
I certainly would be interested in seeing your analysis. You can email it to me at info@real-statistics.com.
2. I have been working on streamlining the analyses that I have been doing so that it is less time-consuming. My latest versions are as follows. Again, I am assuming that I try to maximize the probability of winning within 3 turns, and when failing this maximize the probability of winning in 4 tries, etc. My revised values are
PINES (3 = 34, 4=47, 5=25, 6=6, 7=1, average guesses to solve = 4.05310)
DINES (3 = 34, 4=47, 5=27, 6=3, 7=2, average guesses to solve = 4.04425)
SINEW (3 = 34, 4=44, 5=24, 6=1, 7=1, average guesses to solve = 4.11504)
SILEN (3 = 33, 4=48, 5=24, 6=7, 7=1, average guesses to solve = 4.07080)
SOLID (3 = 28, 4=57, 5=24, 6=2, 7=2, average guesses to solve = 4.05310)
E.g. for SOLID, while my chance of winning within 3 tries is slightly better than yours, my expected number of tries is .06195 worse. Of the 6 guesses analyzed, DINES gives the best results.
3. Yes, I agree that my “Refinements to Best Wordle Second Guesses” are extremely pessimistic. I need to redo this webpage.
Charles
I find I do better if I try to NOT use any correct letters in my second word, rather simply using the most common 5 remaining letters I can in word 2.
Also, Charles, you talk about win probabilities like 21%, 29%, 56%… but isn’t the Times reader average 3.5 words, implying a likely higher win percentage? I’m no wordl wizard, but even my percentage is in the 70%+ range. ??
Hi John,
When you say that your win percentage is in the 70%+ range, are you talking about winning in 6 tries? Or 3 tries, or something else?
Charles
The United States average is about 3.8. My win percentage is about 99.9% (282 of 284). I know several people who have played a comparable number of WORDLES and still have a 100% solve rate.
Starting with mostly consonants seems to make it easier for me to guess words, akin to how the consonants convey the core meaning of words in the Semitic languages, so my first word is often “slant”. If none of those letters is present, my second guess is “biome”. My win rate within three guesses is 29%, half the computer’s ability.
Thank you for an amazing Excel website.
Hello Maxwell,
1. “slant” is a pretty good first guess. With a perfect strategy, you should win 56.67% of the time if you are restricted to using words from the basic dictionary. This would put it in 8th place on the list (tied with “snare”). Your best second guess is “cider” if there is no match. This improves your probability of winning from 21% to 29%.
2. If you can use any word as a second guess, then you should choose “drice” if there is no match after the first guess. Your chance of winning after an initial guess of “slant” is 58.75% assuming that you can choose any word as a second guess.
Charles