The Scheirer Ray Hare Test is the two-factor version of the Kruskal-Wallis test. The assumptions are the same as the Kruskal-Wallis test; in particular, the interaction groups must be equal-sized and contain at least 5 sample members.
Data Analysis Tool
Real Statistics Data Analysis Tool: The Real Statistics Resource Pack provides the Scheirer Ray Hare data analysis tool, as demonstrated in the next example.
Example 1: Repeat Example 1 of Two Factor ANOVA with Replication using the Scheirer Ray Hare data analysis tool (the input data is repeated on the left side of Figure 2).
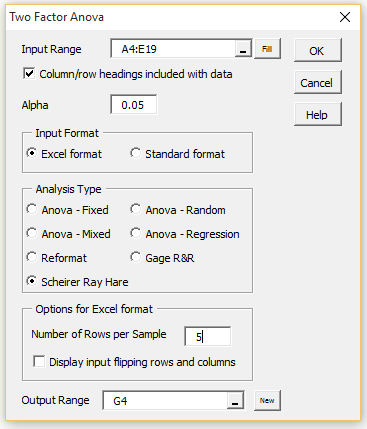
To perform the analysis, press Ctrl-m and double click on the Analysis of Variance option. On the dialog box that appears choose the Anova – two factor option and fill in the dialog box that appears as shown in Figure 1 and press the OK button.
Figure 1 – Two Factor ANOVA dialog box
We first note that if we use the Shapiro-Wilks test on each of the interaction samples we would see that there is no significant departure from normality (although these samples only contain 5 elements) and so we really don’t need to use the Scheirer Ray Hare test, since the usual ANOVA is a more accurate and powerful test. Despite this, we will perform the Scheirer Ray Hare test to show how it is done and to compare the results with ANOVA.
Using the Scheirer Ray Hare Test
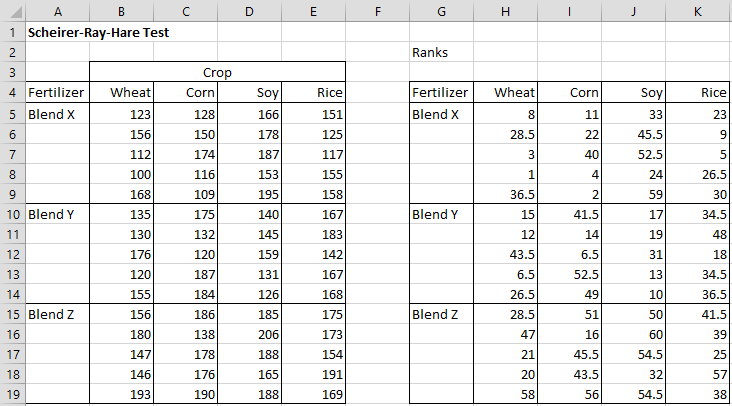
The first thing the Scheirer Ray Hare data analysis tool does is to calculate the ranks for all the input data elements, as shown on the right side of Figure 2. E.g. cell G5 contains the Excel formula =RANK.AVG(B5,$B$5:$E$19,1), or for Excel 2007 users the equivalent Real Statistics formula =RANK_AVG(B5,$B$5:$E$19,1).
Figure 2 – Ranking of the input data elements
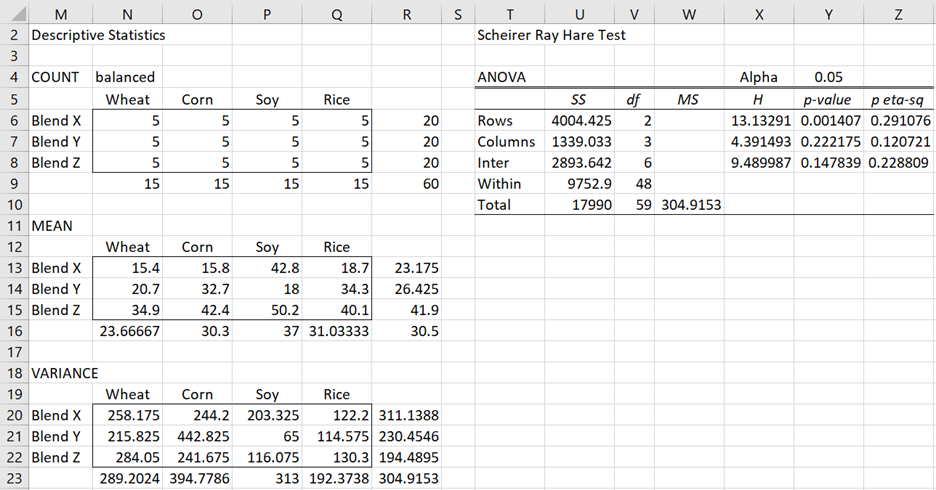
A two factor ANOVA is then performed using the ranks (i.e. range G4:K19) as input, which is then modified as shown in Figure 3.
Figure 3 – Scheirer Ray Hare Test
Results
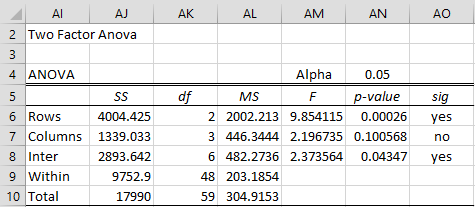
To explain how the output shown on the right side of Figure 3 is obtained, we first show in Figure 4 the usual output for the data in G4:K19 from the Real Statistics two factor ANOVA.
Figure 4 – Two Factor ANOVA on the ranked data
As you can see, the values of SSRow, SSCol, SSInt, dfRow, dfCol, dfInt and dfTot are the same.
The H values in range X6:X8 are calculated by dividing the corresponding SS value by MSTot – e.g. HRow (in cell X6) is calculated by the formula =U6/W10. The Scheirer Ray Hayes test calculates the significance of the Rows, Column and Interaction factors using the fact that the corresponding H statistic has approximately a chi-square distribution with the corresponding df value.
We see, for example, that the null hypothesis for the Rows factor, namely that the three fertilizers are equally effective, is rejected since p-value = CHISQ.DIST(X6,V6) = .001407 < .05 = α. In fact, we see from column Z that only the null hypothesis for the Row factor is rejected.
The main difference from the test using ANOVA is that the Interaction factor (Crops × Blend) is not significant (p-value = .14839), while it is significant using ANOVA (p-value = .04347).
References
Toothaker, L. E. and Chang, H. (1980) On “The analysis of ranked data derived from completely randomized factorial designs”
https://www.jstor.org/stable/1164679
Scheirer, C. J., Ray, W. S., Hare, N. (1976) The analysis of ranked data derived from completely randomized factorial designs
https://www.jstor.org/stable/2529511
Hello. Thanks a lot for the details and it does help.
My data is kinda tricky. I have 2 different factors (A: 4 levels and B: 3 levels) but each sample has only duplicated (n=2). In total, there are only 24 data points (2*12). I want to test the influences of A+B, but due to the small data, I am so helpless about how to continue.
My plan 1 was to operate 2-way-ANOVA (normaliy and variance-homogeneity are passed), and My plan 2 was the Scheirer-Ray-Hare Test. I thought non-parametric might be less strick to data.
Thank you so much! appreciate it
If the assumptions are met, you should use the parametric test.
With small samples, you can only expect so much from the tests.
Charles
Dear Charles,
could you also give an example how to write up the result of a Scheirer-Ray-Hare Test?
Thanks a lot
Andrea
Andrea,
How to write up the results of the test depends on the journal (or other authority) that you are writing for, Usually, the APA is used as a standard, but I doubt that the APA has a template for this test. I suggest that you use the approach for Two Factor ANOVA and modify it accordingly.
Charles
Dear Charles,
I have one between-subject variable (treatment: drug, placebo) and one within-subject variable (emotion: Positive, negative and neutral) in my study. I’m not sure whether i can use the Scheirer-Ray-Hare Test, cause i just find it is suitable for the independent measures. Could you recommend a suitable non-parametric mixed ANOVA method for me?
Best wishes,
Dandan
Tina,
This can be modeled via Repeated Measures ANOVA as described at
https://www.real-statistics.com/one-between-subjects-factor-and-one-within-subjects-factor/
or via MANOVA with repeated measures.
These are parametric tests. I don’t know of a non-parametric version, although I believe that ART ANOVA can be used.
Charles
Dear Charles,
I have a question.
as we see from this post, for each group, they have an equal level size.
if the level size is unbalanced can we use still Scheirer-Ray-Hare Test?
Thanks in advance.
Dandan
As stated on this webpage, “the interaction groups must be equal-sized and contain at least 5 sample members.” The two factors can have a different number of levels (as can be seen in the example).
Charles
Dear Charles,
Thank you!
Here is a question.
I have two groups, one group has two levels, another one group has three levels. The size of each level is different. I have checked the normality and homogeneity of variances. I knew a non-parametric two-way ANOVA should be selected, but I don’t know which one is available in my situation
Could you recommend a suitable non-parametric two-way ANOVA method for me?
Best wishes,
Dandan
Dandan Zhang,
I assume that the normality and homogeneity of variances assumptions were not met. In this case, probably ART ANOVA is your best choice. Scheirer-Ray-Hare might be a reasonable choice.
Charles
How did you arrive with 304.91 as the MStotal? Thanks!
Ah, got it. Nevermind 🙂
Dear Charles,
I performed a Scheirer-Ray-Hare Test as the nonparametric version of a 2-Factor ANOVA in a 6:2 design. You recomend a Mann-Whitney test as post hoc. I didn’t get it managed to run this test on a 2 factorial design. Do you have any suggestions?
Many Thanks
Werner
Hello Werner,
I don-t recall recommending Mann/Whitney as a post hoc test after Scheirer-Ray-Hare test. In any case, which post hoc test to use depends on which factor (Row, Column or Interaction) you plan to study. You can probably use any of the post hoc tests for Two Factor ANOVA provided the assumptions are met.
Charles
Good morning,
Do exist some non-parametric test like Scheirer-Ray-Hare Test but unbalanced (unequal-sized groups)?
In advance, thanks.
José Manuel
Perhaps, but I am not aware of them.
Charles
Dear Dr. Zaiontz,
Thank you so much for such explanation. It helped me a lot since I don’t have access to excel, nor am I able to write an R program. So I have to do the Scheirer-Ray-Hare Test on my own.
My question is: is it really inappropriate to use this test for groups which are not equal-sized? Then would it be okay to use Jonckheere-Terpstra test in default of interaction effect?
Cordially,
Boutheïna
Boutheïna,
Yes, the interaction groups must be equal in size to use the Scheirer-Ray-Hare Test.
The Jonckheere-Terpstra test is a version of the Kruskal-Wallis test where the groups can be ordered. There is no interaction term.
Charles
Thank you for your answer. I’m aware there is no interaction term in the Jonckheere-Terpstra test. I was just wondering if the groups have to be equal-sized too. I guess it must be the case, as a version of the Kruskal-Wallis test.
Dear Charles,
I used Scheirer-Ray-Hare Test to analyze my data and find that there exists interaction effect between two factors (each factor has 2 levels) on the dependent variable. What should I do to further detect the interaction effect?
Thank you very much for your kind help!
May,
See https://www.researchgate.net/post/Can_we_make_a_post_hoc_analysis_after_a_Scheirer-Ray-Hare_test
I would think that you could use pairwise Mann-Whitney tests with a correction (e.g. Bonferroni) for multiple tests.
Charles
Thank you so much for your kind help, Charles. I am going to try the Mann-Whitney U tests.
Kind sir, what could be the procedure for a Scheirer-Ray-Hare Test but with one within subjects factor and one between subjects factor
Gibran,
I don’t know of such a test. You may be able to use regression, although this depends on what assumptions are being violated.
Charles
Dear Charles,
I was just wondering what the appropriate post-hoc test would be to use with the Scheirer-Ray-Hare Test. I know that many including Tukey require that your data is normally distributed and all your groups have a homogeneity of variance, which if your using a non-parametric test it won’t be.
Many Thanks,
Rachel
Rachel,
If you aren’t interested in the interaction factor then you should be able to use any of the Kruskal-Wallis post-hoc tests. But in this case, there probably wasn’t a reason to use Scheirer-Ray-Hare Test in the first place. Regarding post-hoc tests on the interaction factor, the only approach I can think of are multiple Mann-Whitney tests using a Bonferroni correction to reduce experiment-wise error.
Charles
Hello,
How do I put a Bonferroni correction on the Mann Whitney test in real statistics?
wbart
Hello Werner,
If you are performing only one test, then you don’t need to use the Bonferroni correction, but if you are performing say 3 tests, then you need to simply divide the usual alpha value by 3: thus if you usually set alpha = .05 then you will use .05/3 = .016667.
Charles