ANOVA with more than Two Factors

Introduction

Excel doesn’t provide tools for ANOVA with more than two factors. On this web page, we show how to construct such tools by extending the analysis provided in the previous sections. See Real Statistics Support for Three Factor ANOVA for how to perform the same sort of analysis using the Real Statistics Three Factor ANOVA data analysis tool.

Alternatively, see ANOVA using Regression for how to perform ANOVA with any number of factors using regression (either using the standard Excel Regression data analysis tool or the Real Statistics Linear Regression data analysis tool).

We begin by extending the definitions from Two Factor ANOVA with Replication to three factors.

Basic Concepts

Definition 1: Using the terminology of Definition 1 of Two Factor ANOVA with Replication (where we use a and b instead of r and c), define

ANOVA three factors

As before, we can also define the between-group terms. This time there are four types:

SSBetAB = SSA + SSB + SSAB        dfBetAB = dfA + dfB + dfAB        MSBetAB = SSBetAB/dfBetAB

and similarly for SSBetAC, dfBetAC, SSBetBC, dfBetBC,. There is also the following version:

SSBetABC = SSA + SSB + SSC + SSAB + SSAC + SSBC + SSABC

dfBetABC = dfA + dfB + dfC + dfAB + dfAC + dfBC + dfABC

As usual, we can define the error terms:

SSE = SSW          dfE = dfW          MSE = SSE/dfE

Properties

Property 1:

SST = SSA + SSB + SSC + SSAB + SSAC + SSBC + SSABC + SSW

dfT = dfA + dfB + dfC + dfAB + dfAC + dfBC + dfABC + dfW

Proof: The proof is similar to the proof of Property 1 of Two Factor ANOVA with Replication.

Property 2:

image1464 image1465

Similar properties hold for the between AC and BC terms. We also have the following properties about the between ABC term:

image1466

image1467

Property 3: If a sample is made as described in Definition 1 with the xijkl independently and normally distributed and with all \sigma^2_{i.} (or \sigma^2_{.j}) equal, then

image1469

image1470

image1471
Property 4: Suppose a sample is made as described in Definition 1, with the xijk independently and normally distributed.

If all μi are equal and all \sigma^2_{i} are equal then

image1403

If all μj are equal and all \sigma^2_{j} are equal then

image1072

Also, under certain circumstances,

image1472

image1473

Proof: The result follows from Property 1 and Theorem 1 of F Distribution.

Property 5:

image1474

image1475

image1476

image1477

Here terms like (βγ)jk2 are not a product of a beta and gamma term squared. Instead, such a term refers to a single parameter named (βγ)jkwhich is squared.

Test Summary

We use the following tests:

ANOVA three factors testsRecall that the assumptions for using these tests are:

  • All samples are drawn from normally distributed populations
  • All populations have a common variance
  • All samples are drawn independently from each other
  • Within each sample, the observations are sampled randomly and independently of each other

We now show how to conduct the above tests in Excel. Excel doesn’t have a three-factor ANOVA data analysis tool, and so we will need to carry out the analysis using Excel formulas.

Example

Example 1: An Italian research psychologist decides to conduct an experiment to understand the ability of subjects to perform simple tasks when instructed in Italian. She creates 8 sample groups, each with 12 subjects. The three factors are gender (male/female)  of the subject, nationality of the subject (Italian/foreign), and whether the subject performs the task seated or lying down (Seated/Prone). Each participant is given a test to measure their ability to perform the required tasks, with the scores recorded in the table shown in Figure 1. The psychologist wants to know if there are any significant differences between the groups.

Data three factor ANOVA

Figure 1 – Data for Example 1

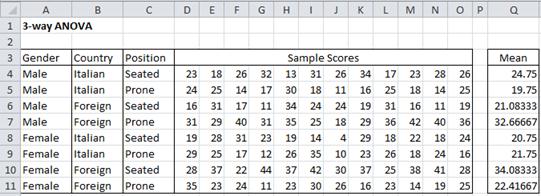
We begin by constructing the tables shown in Figure 2.

Three factor Anova means

Figure 2 – Counts and means for Example 1

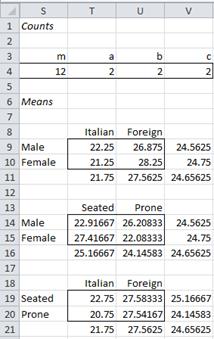
Now using the information in Figures 1 and 2, we can construct the ANOVA analysis as shown in Figure 3.

Three factor ANOVA Excel

Figure 3 – ANOVA for Example 1

We conclude there are significant differences between the nationalities, but no significant differences between the genders or positions. There are also significant interactions between gender and position as well as between all the factors.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Bao, J. (2021) Two-, three-, and four-way ANOVA 
https://sites.pitt.edu/~jub69/material/material/stat1301/Lec/SAS-ANOVA-2.pdf

Laerd (2024) Three-way ANOVA in SPSS statistics
https://statistics.laerd.com/spss-tutorials/three-way-anova-using-spss-statistics.php

Meier, L. (2023) Factorial treatment structure. ANOVA and mixed models: a short introduction using R.
https://people.math.ethz.ch/~meier/teaching/anova/index.html

120 thoughts on “ANOVA with more than Two Factors”

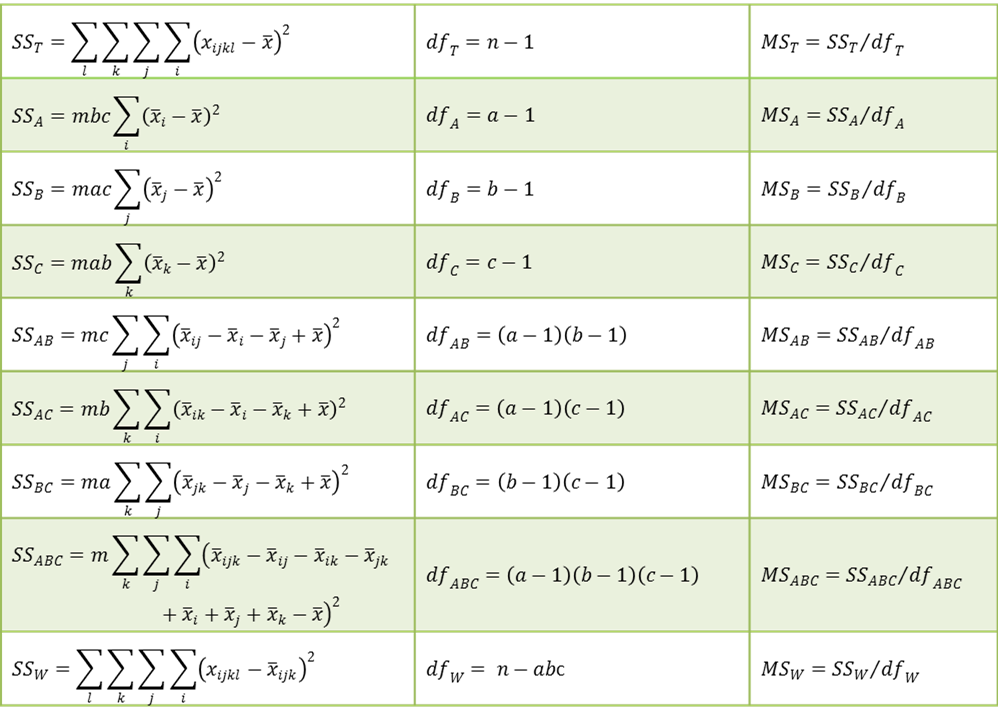
  1. I have three factors, factor 1 =two maize varieties, factor 2=heavy metal levels (0 and 50 mglkg of soil), factor 3= nanoparticle levels(0, 100, 200 and 300 mg/kg of soil). so please let me know what will be my Anova design?

    Reply

  2. Hi, thank you for your tool. I use it for 3 Factor ANOVA with no replication. There’s only one data point subjected to each unique factor combination. Is it possible to assume the data is normal?

    Reply

    • Hi Carolyn-Jean,
      Glad that that you find the tool useful.
      You don’t need to worry about the interaction where there is only one element. You do need to consider normality for the main factors, but keep in mind that ANOVA is relatively robust to violations of normality. Homogeneity of variances is much more important.
      Charles

      Reply

  3. Hi Charles

    I have a question. When I try to estimate a three-way ANOVA, the “SS” values of the interactive variables come out negative and therefore I get “#NUM!” when calculating the p-value. What do you recommend me to do?

    Thank you very much!

    Reply

  4. In the case if a 3-factor ANOVA, how do you estimate the variance related to a specific factor. For instance in a 2 way ANOVA the variance of each factor is estimated using (MSSFactor1 – MSSRes)/(# of factor 2 levels). Am I stating this correctly?

    Reply

  5. Thanks for all the help, comments….trying to self teach on this and its hard reading!.
    I ran the 3 way anova with regression, on data with 3 independent variables, all with 3 levels (High, Mid, Low) and the test result (% yield). When I run the “three fixed factor anova” using excel, the within (error) SS and df are zero, so I get the #DIV/0! error on the F and p-value…when I run with analysis type “anova” I do get the table, but no AxBxC interaction data. Is there something I am doing wrong, or just trying to apply the wrong statistic method to the data that I have?
    Cheers
    Richard

    Reply

  7. Dear Prof. Charles

    I did an exposure experiment with zebrafish and 74 chemicals. For each chemical, there are two concentration levels, and 3 biological replicates (n=20 zebrafish) were conducted for each concentration treatment. In my opinion, there are two factors in this study, the first factor was nominal concentration (control, low, high), the second factor was different chemicals (74). Hence, I used two-way ANOVA with Dunnett test in my study. This work has been submmited to Environmental Health Perspectives. However, the reviwer recommended to do one way ANOVA for 74 times. Could you please give me any professional advice?

    Reply

  8. Hi. Thanks for this wonderful page. It is very useful. I want to cite the first table (three factor example) from this section. Can you provide me source from which table was cited? Is that from your books or articles?

    Reply

    • The formulas for SSW and dfW are shown on the top part of the figure. MSW = SSW/dfW
      For factor A, the formulas for SSA and dfA are shown on the top part of the figure. MSA = SSA/dfA and F = MSA/MSW and p-value = F.DIST(F,dfA,dfW).
      The formulas are similar for the other tests B, C, AxB, AxC, BxC and AxBxC.
      Charles

      Reply

      • Hi Charles, thank you for your reply.
        I now have another issue, for my treatment of a is 2 and treatment of b is 4.
        How can I compute the ss for AB bet?
        Because your example is using the “DEVSQ(T9:U10)*Y9” and this applies to 2 x 2.
        Anthony

        Reply

  11. Hi
    i have collected plant sample ( single plant species) from 3 different sites (A,B &C) for 3 years (2017, 2018 and 2019) and recorded the heavy metal concentrations in plant. i would like to see if heavy metal concentration in plant differ significantly from one site to other and from one year to other.
    Can i use single factor ANOVA ( as i have 9 values) or please suggest which statistical method will be good.

    Reply

  12. Dear Prof. Charles,
    If you allow, I would like to know if there is a 4 way ANOVA?? because I set up an experimentation based on 4 factors (A, B, C and D).
    Is it possible to use as usual SPSS without any changes?

    Yours Sincerely.

    Reply

    • Hello Khokha,
      There is 4-way ANOVA, although it is hard to interpret the results (since these models are quite complicated). I don’t use SPSS and so I don’t know whether SPSS supports 4-way ANOVA.
      Charles

      Reply

    • Hi Khokha

      Did you find out how to make four-way ANOVA by using SPSS?
      Because I am looking for the same method.

      Regards
      Lamisos

      Reply

  13. Dear Charles
    I am trying to study from your web pages design of experimant and used your examples for 2^k Factorial Design Tool. I wrote Alpha o.05 it does not worked then 0 worked and the results were not the same. How can be change alpha on the output. report
    Regards

    Reply

  14. Hello Mr Charles

    I have to run a 3 way mixed factorial ANOVA, where 2 IVs are between subjects, and 1 is within subjects. Could you please guide me on how to set up that data in Excel, so I can perform the test of SPSS accurately.

    Reply

  15. Dear Prof. Charles,

    My study’s case:
    I’d like to know the correlation between the 3 factors (A, B, and C) to Z. The number of subject was 20 and 20 also conditions (combining of the 3 factors). Actually the data were non normal distribution so that I converted it to arcsin transformation and hope can apply the three factors ANOVA. But, I have a problem that the significance value didn’t appear by using SPSS. Then, I’d tried solved manually by following the ways in this site, but I din’t understand how to get the P-value.

    Please help me, really I’m not familiar with statistical data analysis.
    Thank you very much..

    Santi

    Reply

      • Hi Prof. Charles,

        Thank you for the reply,
        I referred to the figure 3 in this page. My questions:
        1. How to get the P-value?
        2. About the degree of freedom (df) value for ABC Bet, why is 7, not 5?

        Thank you,
        Santi

        Reply

        • Hello Santi,
          1. The formulas for the various values of SS are shown in Figure 3. MS = SS/df and F = MS/MSE for each of the sources of variation (A, B, C, AxB, AxC, BxC and AxBxC) where MSE = MS for the error term, i.e. 48.232. Then for each source of variation p-value = F.DIST.RT(F, df, dfE) where dfE = df for the error term, i.e. 88.
          2. As stated earlier on this webpage (just before Property 1), df-BetABC = dfA+dfB+dfC+dfAB+dfAC+dfBC+dfABC = 1+1+1+1+1+1+1 = 7
          Charles

          Reply

  16. Hi Charles,
    I have one situation where am having four independent factors with 3 or 2 levels each and one dependent factor. This experiment is repeated thrice. so now the question is, Can i use 4 factor Anova with similar methodology as 3 factor Anova. The details of factors given below

    Dependent factor-
    (1) Drag value

    Independent factors-
    (1) Material thickness ( 2 levels i.e 2 mm and 3 mm)
    (2) Temperature ( 3 levels i.e 10, 20 ,30 degrees)
    (3) No. of Plates ( 3 levels i.e 1 ,2 or 3)
    (4) Assembly (2 levels i.e Asy. A or Asy. B)

    One more thing it will be helpful if i get some reference for when and how to do nested anova in excel.

    Reply

    • Hi Tiru,
      The methodology for 4 factor ANOVA is similar to that for 3 factor ANOVA. The results are a lot more complicated since you have all kinds of interactions. Suffice it to say that it will likely be quite difficult to interpret the results. With only 3 replications, you shouldn’t expect much added value from all this complexity.
      There are references to nested ANOVA in the Real Statistics Bibliography. If you google nested anova excel you will se various references that may be useful to you.
      Charles

      Reply

  17. Hie sir Charles,
    Your explanation is for independent groups. Can we use the similar approach for 3 way Anova mixed design wherein 2 factors are repeated measures and 1 factor is independent.

    Reply

  18. Dear Charles,
    I’m currently working on my thesis on pasteurization of 2 different types of milk(goat and cow) using 8 different bacteria. The purpose is to see how well the bacteria can grow in these different temperatures.
    I’m wondering if you could help me determine which statistical analysis I should use. Please forgive me if my explanation isn’t clear – I’m new to this and haven’t had much experience using statistics!
    As data, i have, temperature and pH with 2000 data points.
    I have done experiments on 4 different temperatures(0,30,75,80) and done repeats of these.
    I have calculated the time and value of max slope it takes for the pH to start drop below 6,2 (when the milk starts to coagulate).
    My question is, how can I best describe the differences and I’m also required to show this graphical, is it possible?, if so which type and what should be on the different axis?

    Hope you can help..
    Best Regards
    Saad Khan

    Reply

  19. Hi Sir!
    I am currently working on my research regarding the effect of the three parameters on the degradation percentage using photocatalytic process.

    This is how it goes.
    I have a three variables: Concentration(8 ppm and 12 ppm), Catalyst Loadings(500mg and 1000mg) and Time(1hr and 2hr). The sample was obtained in triplicate.
    I am to determine the significance of the three parameters on the degradation and to know the interaction of the variables

    Sir, I am new at doing this statistics analysis and I don’t know how I am going to be presenting my data. Moreover, can you tell me if I can use SPPS, Minitab or Excel on analyzing my data? I am so confused at the moment. Sir, I am so in need of your help. I hope you can teach me about this. Any response from you will be greatly appreciated. Thank you Sir!

    Ronald

    Reply

  20. Hello Charles,

    I was wondering if you could help me determine what is the best statistical analysis for my work.

    I am studying the effect of treatment A (at 3 different concentration), treatment B (at 2 different concentration) and the combination of treatment A and treatment B on gene expression. So I am looking at the individual effect of both treatment and comparing if the combination of A + B at lower concentration induces the desired therapeutic effect of A at the highest concentration. For exemple I have group 1 (A at 50 µM), group 2 (A at 250 µM), group 3 (A at 500 µM), group 4 (B at 25 µM), group 5 (B at 50 µM), group 6 (A at 50 µM and B 25 µM), group 7 (A at 250 µM and B at 25 µM), group 8 (A at 500 µM and B at 25 µM), and so on with a control group. Lets say the desired therapeutic effect we want is with A-500 µM and we want to lower the dose with the addition of molecule B. We want to see if treatment A-500 µM is equivalent to treatment A 250µM + B-25µM or B-50µM. Would it be a two way anova ? Is it with repeated measure in each treatment group I have 4 replicates?

    Thank you for your input.

    Reply

    • Ariane,
      If I understand correctly, you have 8 treatment groups (perhaps more) plus a control group. I presume that no subject is more than one group (in which case you don’t have a repeated measures model – repeated measures is not the same as a model with replications).
      One way to view this is as two factor Anova with factors A and B. The levels for A are 0, 50, 250, 500 (note that I added a zero level) and the levels for B are 0, 25, 50 (once again adding a zero level). This should work provided all the possible interactions between A and B levels are modelled (I am not sure whether this is true).
      Checking whether treatment A-500 µM is equivalent to treatment A 250µM + B-25µM or B-50µM can be done via contrasts in the follow-up analysis. Of course, if this is all you want to test, then you could simply create three groups with just these treatments and use one-way ANOVA.
      Charles

      Reply

      • Hello Charles, thank you for the reply.

        Would an anova with repeated mesure be if I did the same experiment 3 times and wanted to combine them for the analysis ?

        Reply

        • Ariane,
          This depends on the details. Since you are combining the 3 measurements, probably you wouldn’t need to use the repeated measures version of ANOVA.
          Charles

          Reply

  21. Hi Charles,

    I’m wondering if you could help me determine what statistical analysis I should use for the following example. Please forgive me if my explanation isn’t clear – I’m new to this!

    I’m studying seizure spread from one brain site (seizure focus) to several others (propagation sites), for the purposes of understanding why some seizures impair consciousness and others do not. For this experiment, I have three seizure foci. This is the independent factor. Subjects are grouped based on their seizure foci. For each subject, I’m recording from five sites different sites. These recording/propagation sites are the within-subjects factor. I record from the same five sites for each of the seizure foci. Recording takes place over the course of 7 days. I record from the propagation sites each day, for 7 days. The dependent variable is seizure duration.

    In summary, there are three factors: seizure focus (independent), propagation/recording site (within-subject factor), and recording day.

    Based on the data (which I can provide to you), I’d like to determine whether there is a main effect for 1) seizure focus, 2) propagation/recording site, and 3) recording day. I’d also like to study interactions between the three factors. What statistical test would be appropriate for this?

    Thanks in advance,
    Jabir

    Reply

  22. Good day Sir,

    Thank you so much for your add-in, this has made my computations easier.
    I just have a question regarding negative sum of squares for two-way interactions. The value of SS for AB interaction in my results turn out to be negative, so that the p-value cannot be computed. May I know if this is possible?

    Thanks in advance sir and have a nice day.

    Reply

    • Janine,
      The sum of squares should never be negative. If you send me an Excel file with your data and calculations, I will try to figure out what the problem is. You can find my email address at Contact us.
      Charles

      Reply

  23. sir, i am trying to develop a model which can group the levels of factors from severe to moderate to low. 3 factors(rpm, load, ambient humidity) are there each with 3 levels.output(response) is failure rate of bearings. the combination of factors with different levels is said to be severe then other combination of levels for factors if failure rate for earlier one is greater than second combination.
    sir, i want to know which statistical method should i use to model it and test the hypothesis.
    My problems falls in category(multi factor ANOVA) or not whether i should use multi regression model or not.sir, i am relatively new in statistics field your response will be highly important and beneficial to solve and approach this problem statistically correct.

    Reply

      • sir ,
        i want to test that whether the degradation rate for mechanical bearing is greater for level combination A (LA,LA,LA) than level combination B (LB, LB,LB) for three factors or is it less.

        Reply

  24. DEAR Charles
    I have a situation where not sure how to deal, and maybe you can suggest something.
    I have three factors 1: climate with three levels, 2. Cultivars with two levels and 3. Irrigation with two levels. I have physiological measurements from plants on two different occasions (lets say day 1 and day 3). I want to know if the measurements done on day 1 were statistically different from day 3. Can I include time (measurement time with two levels viz. day 1 and day 3) as a fourth factor to perform a 4-way ANOVA? I can not do ANOVA with repeated measures because measurements on day 1 and day 3 were not exactly done on same plants/leaves but of course from the same group of plants.

    Thanks

    Reply

    • Adil,
      With more than three factors it is very difficult to interpret the results. I suggest that you create separate models with a maximum of three factors, especially if you don’t need to compare all the factors with each other.
      I am not sure how to deal with the following issue: “I can not do ANOVA with repeated measures because measurements on day 1 and day 3 were not exactly done on same plants/leaves but of course from the same group of plants.” Perhaps nested ANOVA or some other ANOVA approach would work, but this would probably depends on some of the details of your situation. If the same group of plants share essential characteristics, then perhaps even repeated measures ANOVA would be appropriate. How this is handled may also depend on how others in your field have handled such situations in the past.
      Charles

      Reply

  25. Hi Charles,
    thanks for all the brilliant explanations and the excel add-on which are really saving me hours of work.
    I’ve run a 3 way anova recently (operators, days, batches) and I get the same table from your figure 3 on this page but how do I then go on to calculate the reproducibility and repeatability in the same way that it is done on the 2 way anova?
    Thanks
    John

    Reply

  26. sir, your site is extremely useful for researchers like me who had poor knowledge in statistics. but I have some more guidance in feeding the data. Kindly help me. I have collected the no. of egg ribbons of a molluscan organism in two different sites, from three tidal levels ( sub sites ) in each site for 24 months in 25 cm2 area. Prof Hodgson from South Africa had done the same work earlier and performed 3-factor nested ANOVA keeping time and site as fixed factors and sub-sites as random factor. My problem is following Your figure1 in example 1, which data I should enter as A,B,C columns of excel sheet, ofcourse I will enter the no. egg ribbons from col. D onwards. please help me to enter the data following Hodgson’s fixed and random factors.

    Reply

    • If I understand correctly site as a fixed factor and sub-sites nested in site. Since you say this is a random factor, I understand that there are more than 3 possible tidal sub-sites, with 3 chosen at random. Is this correct?
      Regarding time, it sounds like you take multiple readings at different points in time. Is this correct? If so, then Time is a repeated measures factor.
      If I have captured the situation correctly, then the Real Statistics software doesn’t quite support this case.
      Charles

      Reply

  28. the programe shows the follwoing error: Alpha must be a number between 0 and .5
    I selected 0.05 but even it shows the same error

    Reply

    • Garapati,
      Which data analysis tool were you using?
      In the meantime, I suggest that you enter the value 0 for Alpha and then change its value on the output report.
      Charles

      Reply

  29. Hi Sir Charles!

    I have my thesis that works like this:

    FACTORS
    A = Concentration: 3 levels
    B = Time: 6 levels (7days, 6days, 5days for 25 deg C) (5, 10 and 15 minutes for 100 degC)
    C =Temperature: 25degC and 100 degC (2 levels)

    The problem is when I manually calculate the three way anova of this, there will be no intersection of B and C at certain points; that is, when the temp. is 25 the intersection to time is only 7, 6 and 5 days and when the temp. is 100, the intersection to time is only 5, 10 and 15 minutes. It makes the value of B x C negative and ruins the whole ANOVA table (no values for p-value can be obtained)

    I also tried using the Real Statistics Data Analysis Tool on my Excel and yielded the same results. My question is: is the three way anova applicable to my case? Is there any more statistical treatment that I can use to find out which of the factors influences the variable on my thesis. I badly need you help sir! Thank you very much

    Reply

  30. Hello Dr. Charles!

    Can you please give me a copy of the excel file =(
    I really wanted to study it on excel, especially the last picture (construction of ANOVA table)

    Thanks!

    Reply

    • Mat,
      The approach to 4 factor Anova is similar to 3 factor Anova, excepty that it is more complicated and difficult to interpret since now you have the factors A, B, C, D, AxB, AxC, AxD, BxC, BxD, CxD, AxBxC, AxBxD, AxCxD, BxCxD and AxBxCxD.
      A 2^k factorial design has k factors, where each factor has two levels.
      Charles

      Reply

  33. Hi Charles,
    Thanks for the detailed explanations and for the extremely helpful website. I only took an introductory stats class quite some time ago and I was only taught the one-way ANOVA, so please excuse my ignorance on this matter. I’m wondering if we can eliminate some factors based on ANOVA analysis on limited preliminary data for a system involving many possible factors. As an example, I’ll use a case with 2 factors. Please bear with me and my lengthy questions.

    Say we are investigating the effect of 2 factors, A and B, on a dependent variable. However, there is no control over the values of these 2 factors. For example, factors are the waiting time for a student before giving a presentation and the length of the presentation time and the dependent variable is the grade they received.

    Two questions:
    1/ We have too much variations for the values of these factors. Say, none of them are the same (10, 15, 17, 12, etc). Do we lump the values together and make them into categorical – e.g., low, mid, high (or even numerical based on their average)? Would this introduce large errors in the calculation?
    2/ If the data that we obtained do not actually “fill” the table completely, could we still calculate the sum of squares between these factors as if they are 2-way ANOVA? For example, we only have data for:
    a) Students who have waited for a “short” time and presented either a ” mid-length” or a “long” presentation
    b) Students who have waiting for a “mid-length” time and presented either a “short” or a “mid-length” presentation
    c) Students who have waiting for a “long” time and presented either a “short” or a “long” presentation

    Or is there an alternative statistical test in order to investigate whether these factors affect the scores at all?

    Would greatly appreciate your advice. Thank you!

    Reply

    • Chelsea,
      I only partially understand the situation you are describing, but, in any case, here are a couple of observations:
      1. To use ANOVA, the independent variables need to be categorical. If they aren’t then by necessity you need to lump some of them together.
      2. If the data doesn’t completely fill the table (or if you have an unequal number of sample elements in the cells of the table), then you have an unbalanced model. You can still analyze such models using ANOVA (although under the covers the analysis is regression). You can learn more about this at the webpage: Unbalanced ANOVA.
      Charles

      Reply

      • Thank you for your answer, Charles. Very much appreciated.

        I am thinking along the line of how to identify which factors in experiments affect the result and which don’t (whether or not there is a correlation between each of these factors and the result). Problem is these factors aren’t controllable, thus the effect of each factor cannot be isolated from the others. Sorry for not expressing myself clearly. I really gotta do more reading on various stats method.

        Thanks again! Your website has been a great help!

        Reply

  34. Dear Dr Charles
    This is an excellent tutorial.
    I want calculate ANOVA for the following data.
    The data provided is the gray rational grade values for input parameters 4 for 3 levels
    PARAMETER LEVEL-1 LEVEL-2 LEVEL-3
    VOLTAGE V 0.450339471 0.634585192 0.71200671
    PULSE OFF 0.617898144 0.557872095 0.621161134
    PULSE ON 0.607522282 0.487965309 0.701443781
    CURRENT 0.501263495 0.665427997 0.630239881
    The total DF value is equal to 8.
    Thank You

    Reply

    • Dear Srikant,
      The website explains how to address these sorts of problems. The Real Statistics software makes it easy for you to do so. I am afraid it is up to you to do the rest.
      Charles

      Reply

  35. In figure 3, I understand everything except the computation necessary to find the P-Value. What did you do to find that number?

    Reply

      • Hi Charles,

        thank you the calculations. they are really helpful.

        I am unable to find how to calculate the F value and P value as the figure 3 does not show the formulas.

        Can you help?

        Reply

        • As always F for any factor is equal to MS for that factor divided by MS for the error term. E.g. for factor A, F is MSA/MSW. The p-value is FDIST(F,df1,df2), where df1 is the degrees of freedom for that factor and df2 is the degrees of freedom for the error term.
          Charles

          Reply

  36. pls can you help out with this question
    an experiment consists of two factors,A and B ,each at 3 levels
    a.write the appropriate ststistical model
    b.specify the appropriate hypothesis to be tested
    c.give a skeletal Anova for presenting results of the analysis of data fro m the experiment

    Reply

  37. Hi!

    I have a Three-Way Within-Subjects ANOVA. Independent Variable 1 has 2 levels, Independent Variable 2 has 2 levels, and Independent Variable 3 has 3 levels. I have 4 subjects, who went through all the 12 conditions.

    My question is that I have drawn up the ANOVA table in excel as followed from your website, and I found that the 3 main effects, 3 two-way interaction effects, 1 three-way interaction effect all share the same error value, which is the Error(Within). But isn’t a Repeated Measures table supposed to have individual Errors for each effect, just like the Two-way Within Subjects ANOVA table drawn on your website?

    Please enlighten me on this, thank you!

    Reply

    • Rebecca,
      The Three Factor ANOVA shown on the website does not deal with repeated measures. In order to handle a three factor repeated measures ANOVA you need a four factor model which extends the two factor repeated measures ANOVA described on the website. Since this model is complicated to calculate and even more complicated to interpret, I thought that at least for now it was better not to include on the website. As you said, this model would need a separate error term for each effect.
      Charles

      Reply

  38. Respected sir,
    Kindly advice me to solve three factor analysis arranged in split plot design i.e.,
    Main plot : First factor- three levels of irrigation (3)
    Subplot: Factorial combinations of fertilizer and time application (3×2)
    Second factor – three levels of fertilizer (3)
    Third factor – two levels of time of application (2)
    WAITING FOR U RESPONSE

    Reply

    • Kiran,
      It is not so hard to modify the three factor ANOVA design described on the referenced webpage for split plot design, but I haven’t done this yet. I hope to get to this in one of the next few releases. Stay tuned.
      Charles

      Reply

  39. hello,
    i tried using 3 factor anova and because i have 12 conditions my ‘within’ & ‘df’ cell is zero.so all of my f crit, f and p values are not defined. how do i fix this?

    also i am not sure how to interpret the results of 3 factor anova, for example which factor has the significant effect? and so on. is there a hand out i can read more on the interpretation of the 3 way anova results because i can;t seem to be able to find anything online.

    thanks
    icell

    Reply

    • icell,
      If all the values are zero, it probably means that your sample is too small.
      The interpretation of the results of three factor anova is quite similar to that of two factor anova, except that it is more complicated since you not only have an extra factor, but you have three more interactions. For Example 1 on the referenced webpage, there is an explanation as to which factors have a significant effect (as always you just need to see if the p-value for that factor is less than alpha).
      Charles

      Reply

  41. Dear charles,
    I still confuse to get anova three way table by using excel. I have no idea to calculate p-value and Fcrit. Could you give some explanation Charles?
    Thank you

    Reply

    • The explanation can be found in Figure 3. Perhaps, you can tell me which formulas in that figure are not clear.
      Charles

      Reply

  42. Why is the denominator when calculating F always between(within)? Would the calculations change at all if two of the factors were random? If so, how? Thanks for the explanations.

    Reply

    • Linda,

      The count for A is calculated via the formula =S4*U4*V4
      B via =S4*T4*V4
      C via =S4*T4*U4
      AB Bet via =S4*V4
      AC Bet via =S4*U4
      BC Bet via =S4*T4
      ABC Bet via =S4

      Charles

      Reply

    • Stanly,
      As you can see in the Formulas for SS column in Figure 3 each DEVSQ formula is multiplied by a count value (e.g. for SSA this is Y6 which is equal to 48). For SST you don’t need to multiple the DEVSQ formula by anything (or equivalently you multiply it by 1).
      Charles

      Reply

  45. can you guide me on how to obtain the count data? especially count for AB bet, BC bet and so on.
    I am trying to do a three way anova and my a, b, and c factors each has 2, 3 and 4 variables respectively and 300 sample size per row. I can’t seem to get through on how to get the count data. your help is very much appreciated. thanks alot.

    Reply

    • Max,

      If I understand your question correctly, a = 2, b = 3, c = 4 and m = 300. This would mean that the total sample has size n = abcm = 7200. If this number is too high, then probably the m value is lower.

      Assuming the above is correct, dfBetAB = dfA + dfB + dfAB = (a-1) + (b-1) + (a-1)(b-1) = 1+2+2 = 5.

      Charles

      Reply

  47. This is an excellent tutorial.

    However, I am confused about how the counts are derived and what they mean for. (Y4:Y17) and (S3:V4).

    I would greatly appreciate an explanation.

    Thanks

    Reply

    • Sorry about the comment. It appears that the counts are derived from m, a, b, c, the number of levels, and the number of participants in each group. I’m rusty on anova calculations, but this tutorial helps a lot 🙂

      Reply

      • No problem. You are correct that the counts are derived from m, a, b, etc. Feel free to comment, even about simple things. It is better to ask questions to clarify things if necessary.
        Charles

        Reply

Leave a Comment