Three-Factor ART ANOVA

Basic Concepts

On this webpage, we describe how to conduct aligned rank transform (ART) ANOVA with three factors.

Since we have three factors, we assume that the data can be represented as x_ijkh where i, j and k represent the three factors and h represents replications.

For the i factor, we adjust each data element as follows:

The adjustments are similar for the j and k factors, For the interaction of the i and j factors, we adjust each data element as follows:

The adjustments are similar for the jk and ik interactions, For the interaction of the i, j and k factors, we adjust each data element as follows:

Now we conduct seven separate ANOVA analyses, one for each effect. The data for these are the ranked values of the x′_ijkh. We show how this is done for the A factor, but first, we describe the following function.

Worksheet Functions

Real Statistics Function: The Real Statistics Resource Pack supports the following array function:

Std3Art(R1, head): takes the data in R1 in standard three-factor ANOVA format (i.e. a four-column array whose first three columns consist of A, B and C factor labels and whose last column consists of the corresponding values of the dependent variable) and returns an array with ten columns, the first three columns are identical to the first three columns of R1 and the other columns are the ART ranks for the A, B, C, AB, AC, BC and ABC factors; if head = TRUE (default FALSE) then both R1 and the output contain column headings.

Example

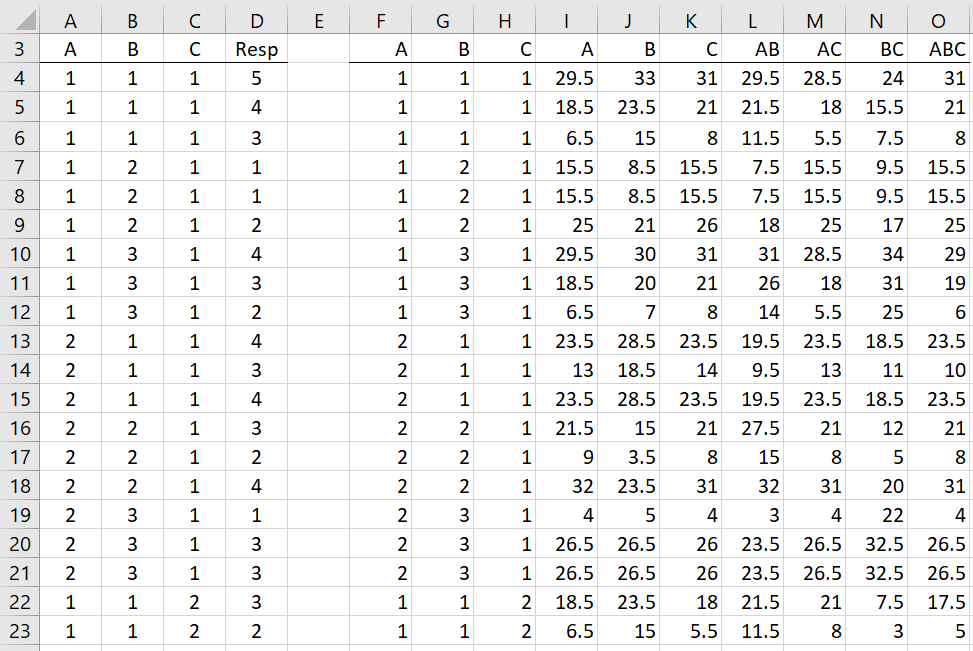
Example 1: Show how to calculate the p-value for the A factor of three-factor ART ANOVA for the data shown in columns A, B, C and D of Figure 1 (only the first 20 of 36 rows is displayed).

Figure 1 – Aligned Ranks

In this example, factors A and C have two levels and factor B has 3 levels. Range F3:O39 contains the aligned ranks as calculated by the array formula =Std3Art(A3:D39,TRUE). We now use Real Statistics’ Three-Factor ANOVA data analysis tool based on the input range F3:I39 in standard format, as shown in Figure 2.

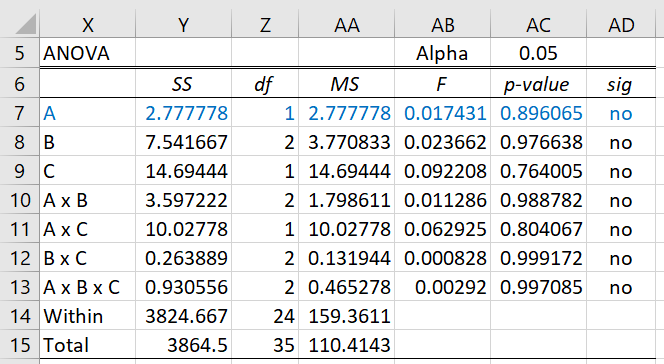
Figure 2 – Three-Factor ANOVA on ART data for factor A

We see from the figure that factor A is not significant. We can ignore all the output except that associated with factor A. Finally, we can next perform similar analyses for the other factors.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Wobbrock, J. O., Findlater, L., Gergle, D., Higgins, J. J. (2011) The Aligned Rank Transform for Nonparametric Factorial Analyses Using Only ANOVA Procedures. Conference: Proceedings of the International Conference on Human Factors in Computing Systems, CHI 2011, Vancouver, BC, Canada
https://faculty.washington.edu/wobbrock/pubs/chi-11.06.pdf

Leys, C. and Schumann, S. (2010) A nonparametric method to analyze interactions: The adjusted rank transform test
http://cescup.ulb.be/wp-content/uploads/2015/04/Leys_and_Schumann_nonparametric_interactions.pdf