Granger Causality

Granger Causality

As we have learned on many occasions, correlation doesn’t necessarily imply causality, and while we can measure the degree of association between two variables, i.e. correlation, it is harder to determine whether one variable causes another variable.

Although generally, we don’t believe that a present or future event can cause a past event, we do believe that it is possible that a past event can cause a present or future event. This is the impetus for the Granger’s Causality test on time-series data that gives evidence that variable x causes y. Whether this test really demonstrates causality is open to debate, and so we will use the phrase “x Granger-causes y” instead of “x causes y”.

As we will see, x Granger-causes y when the prediction of y is improved by the inclusion of past values of x.

Granger Causality Test

The test is based on the following OLS regression model:

Here, the α_j and β_j are the regression coefficients and ε_i is the error term. The test is based on the null hypothesis:

 H₀: β₁ = β₂ = … = β_m = 0

We say that x Granger-causes y when the null hypothesis is rejected.

We use the usual F test described in Adding Extra Variables to a Regression Model to determine whether there is a significant difference between the regression model shown above (the full model) or the reduced model, based on the null hypothesis, without the β_j terms (i.e. where all the β_j = 0).

There we demonstrate two equivalent forms of the test:

Here, all the terms are based on the full model with the exception of SS′_E and R_r², which are based on the reduced model.

If the p-value for this test is less than the designed value of α, then we reject the null hypothesis and conclude that x causes y (at least in the Granger causality sense).

Assumptions

The Granger Causality test assumes that both the x and y time series are stationary. If this is not the case, then differencing, de-trending, or other techniques must first be employed before using the Granger Causality test.

Note that the number of lags, i.e. the value of m, is critical, in that different values of m may lead to different test results. One approach to selecting an appropriate value for m is to choose the value that results in the full model with the smallest AIC or BSC value.

It is possible that causation is only in one direction, or in both directions (x Granger-causes y and y Granger causes x) or in neither direction.

Examples

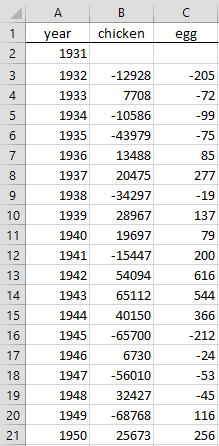
Example 1: Figure 1 shows the egg production and chicken population (including only those birds related to egg production) for the years 1931 to 1970. Determine whether the amount of egg production Granger-causes the size of the chicken population or the chicken population Granger-causes the amount of egg production, or both or neither. This example is a tongue-in-cheek exploration of the common question, “Which came first: the chicken or the egg”?

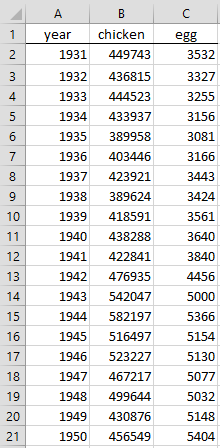
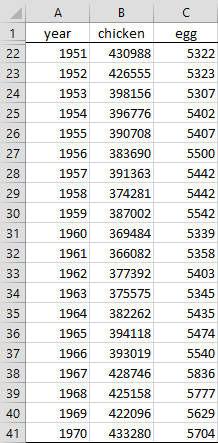
Figure 1 – Chicken and Egg production

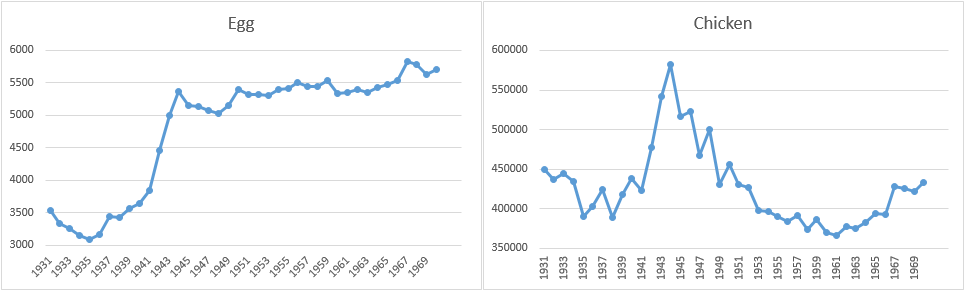
 A plot of both time series (see Figure 2) shows that neither series is stationary.

Figure 2 – Time series plots 

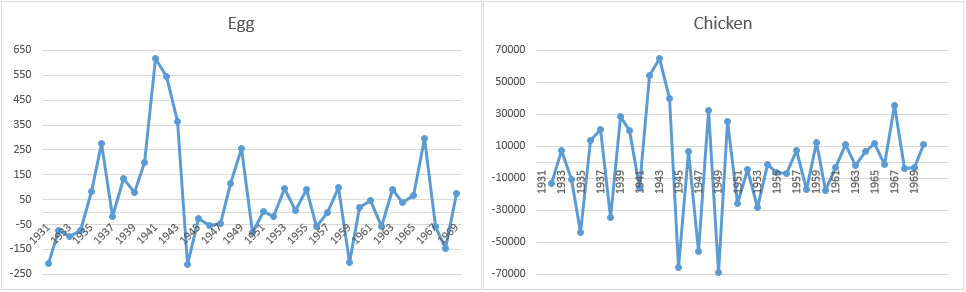
As a result, we will instead study the first differences of each time series. The data and time series plots for these are shown in Figures 3 and 4.

Figure 3 – Differenced time series

Figure 4 – Plots for differenced time series 

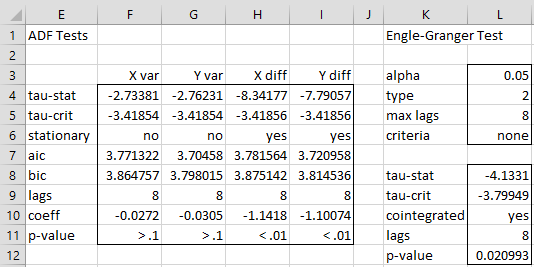
The plots suggest that the time series may be stationary. This result is confirmed by using the ADFtest (see Augmented Dickey-Fuller Test) as shown in Figure 5.

Figure 5 – ADF tests

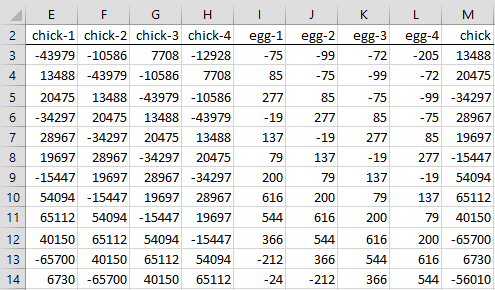
We now show how to determine whether Chickens Granger-cause Eggs for lags = 4. To do this we perform regression on the X data in range E2:L37 of Figure 6 and Y data in range M2:M37 (only the first 12 of 35 rows are shown).

Figure 6 – Setup for regression 

We now calculate the p-value of the Granger Causality Test for this data, as shown in Figure 7.

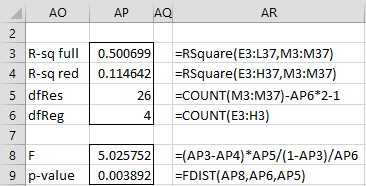
Figure 7 – Test for Granger Causality

Here we use the Real Statistics function RSquare on the full model (cell AP3) as well as the reduced model (AP4), although we could have gotten all the values in the figure by actually conducting the regression.

Since p-value = 0.003892 is small, we conclude that Eggs Granger-cause Chickens for lags = 4. Alternatively, we could have calculated the p-value by placing the Real Statistics formula =RSquareTest(E3:L37,E3:H37,M3:M37) in cell AP9.

Worksheet Functions

Real Statistics Functions: The Real Statistics Resource Pack supports the following two functions that make it easy to determine whether the time series in the column array Rx Granger-causes the time series in the column array Ry at the specified number of lags.

GRANGER(Rx, Ry, lags) = the F statistic of the test

GRANGER_TEST(Rx, Ry, lags) = p-value of the test

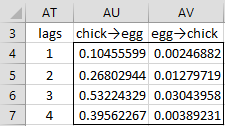
We can use the GRANGER_TEST function to determine whether Eggs Granger-causes Chickens and vice versa at various numbers of lags, as shown in Figure 8.

Figure 8 – Granger Causality Tests 

For example, cell AV7 contains the formula

=GRANGER_TEST(C3:C41,B3:B41,AT7)

with references to the data in Figure 3, and produces the same results as in Figure 7.

We see from Figure 8 that Eggs Granger-cause Chickens, but the reverse is not true.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

Reference

Thurman, W. N. and Fisher, M. E. (1988) Chickens, eggs, and causality, or which came first? American Journal of Agricultural Economics. Vol. 70. No. 2.
http://web.pdx.edu/~crkl/ec571/eggs.pdf