Basic Concepts
A random walk time series y1, y2, …, yn takes the form
yi = δ + yi-1 + εi
where
εi ∼ N(0, σ2)
cov(εi, εj) = 0 for i ≠ j
If δ = 0, then the random walk is said to be without drift, while if δ ≠ 0, then the random walk is with drift (i.e. with drift equal to δ).
It is easy to see that for i > 0
It then follows that E[yi] = y0 + δi, var(yi) = σ2i and cov(yi, yj) = 0 for i ≠ j. The variance values are not constants but vary with time i, and so this type of time series is not stationary. Also, the mean values are constant only for a random walk without drift.
Note too that since cov(εi,εj) = 0 for i ≠ j, it follows that
Note that the first difference zi = yi – yi-1 of a random walk is stationary since it takes the form
which is a purely random time series.
Plot
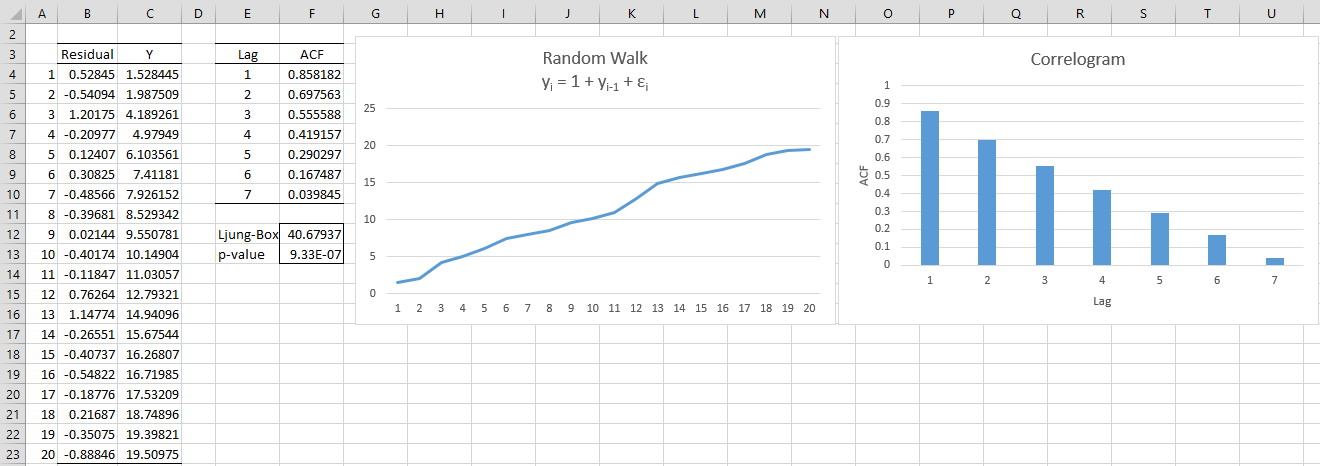
Example 1: Graph the random walk with drift yi = yi-1 + εi where the εi ∼ N(0,.25). (The standard deviation is .5.)
The graph is shown in Figure 1. All the cells in column B contain the formula =NORM.INV(RAND(),0,.5), cell C4 contains the formula =1+B4 and cell C5 contains the formula =1+B5+C4.
As we can see, the graph shows a clear upward trend and the ACF shows a slow descent.
Figure 1 – Random Walk
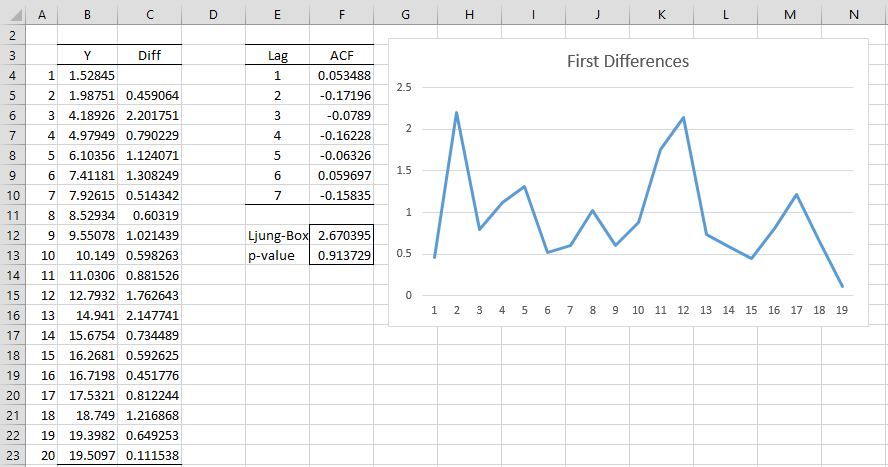
First differences are taken between the y values as shown in Figure 2. E.g. cell C5 contains the formula = B5-B4 (where column B replicates the values in column C from Figure 1). We see from the chart that the trend has been eliminated. We also see from the Ljung-Box test (cell F13) that the ACF values for the first 7 lags are statistically equal to zero, consistent with a purely random process.
Figure 2 – First differences of a random walk
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Greene, W. H. (2002) Econometric analysis. 5th Ed. Prentice-Hall
https://www.ctanujit.org/uploads/2/5/3/9/25393293/_econometric_analysis_by_greence.pdf
Gujarati, D. & Porter, D. (2009) Basic econometrics. 5th Ed. McGraw Hill
http://www.uop.edu.pk/ocontents/gujarati_book.pdf
Hamilton, J. D. (1994) Time series analysis. Princeton University Press
https://press.princeton.edu/books/hardcover/9780691042893/time-series-analysis
Wooldridge, J. M. (2009) Introductory econometrics, a modern approach. 5th Ed. South-Western, Cegage Learning
https://cbpbu.ac.in/userfiles/file/2020/STUDY_MAT/ECO/2.pdf
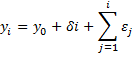
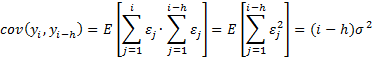
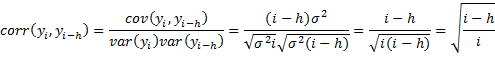
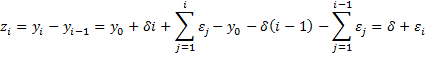
Hello Charles,
Your website is extraordinary. Excellent. I am understanding Time Series in a better way.
Hi Samir,
Glad I could help.
Charles