A purely random time series y1, y2, …, yn (aka white noise) takes the form
yi = μ + εi
where
εi ∼ N(0, σ2)
cov(εi, εj) = 0 for i ≠ j
Clearly, E[yi] = μ, var(yi) = σ2i and cov(yi, yj) = 0 for i ≠ j. Since these values are constants, this type of time series is stationary. Also, note that ρh = 0 for all h > 0.
Example
Example 1: Simulate 300 white noise data elements with mean zero.
Using the formula =NORM.S.INV(RAND()) we can generate a sample of 300 white noise elements, as displayed in Figure 1.
Figure 1 – White Noise Simulation
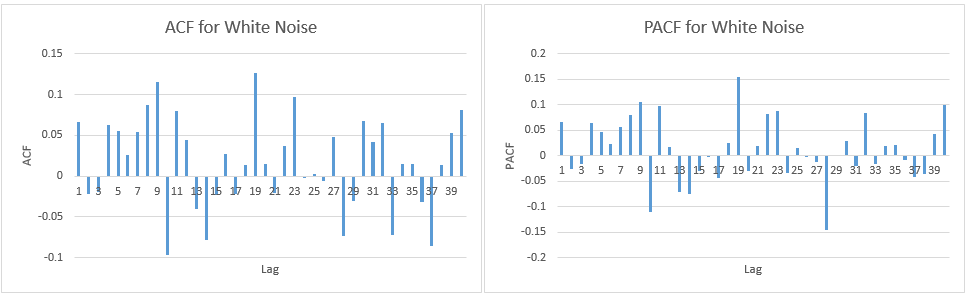
We see that there is a random pattern. Using the techniques described in Autocorrelation Function and Partial Autocorrelation Function we can also calculate ACF and PACF values, as shown in Figure 2.
Figure 2 – ACF and PACF for White Noise simulation
Testing
Although the theoretical ACF values are ρk = 0 for all k > 0, the sample values rk won’t necessarily be exactly 0, as we can see from the left side of Figure 2. Based on Property 3 of Autocorrelation Function
rk ∼ N(0, 1/n)
Since n = 300, a 95% confidence interval for rk is
0 ± NORM.S.INV(.025)/SQRT(300) = ±0.11316
Figure 2 shows 40 values for rk. We would expect that about 40(.95) = 2 of these values would be outside the 95% confidence interval. In fact, two ACF values are outside this range, namely r9 = .11842 and r19 = .13366.
Using the Ljung-Box test, we see that none of the 40 ACF values is significantly different from zero:
p-value = CHISQ.DIST.RT(46.2803,40) = .229 > .05 = α
We can perform similar tests for the PACF values.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Greene, W. H. (2002) Econometric analysis. 5th Ed. Prentice-Hall
https://www.ctanujit.org/uploads/2/5/3/9/25393293/_econometric_analysis_by_greence.pdf
Gujarati, D. & Porter, D. (2009) Basic econometrics. 5th Ed. McGraw Hill
http://www.uop.edu.pk/ocontents/gujarati_book.pdf
Hamilton, J. D. (1994) Time series analysis. Princeton University Press
https://press.princeton.edu/books/hardcover/9780691042893/time-series-analysis
Wooldridge, J. M. (2009) Introductory econometrics, a modern approach. 5th Ed. South-Western, Cegage Learning
https://cbpbu.ac.in/userfiles/file/2020/STUDY_MAT/ECO/2.pdf

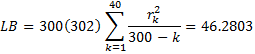
In Page https://www.real-statistics.com/time-series-analysis/stochastic-processes/autocorrelation-function/ there are 3 tests for ACF. Which one is equivalent to the one suggested here?
(and how to choose among them if you just test a single lag , namely a seasonality lag)
If I understand your question, this webpage uses the test in Property 5 (Ljung-Box).
I don’t have an opinion as to which is the best test to use. Regarding seasonality, see
https://stats.stackexchange.com/questions/504861/influence-of-seasonality-on-unit-root-tests
Charles
hi, charles – i reckon the link is over my capacity…so plz tell me can you use single ACF instead of a full blown correlogram to judge if the (given) seasonality is worthy of adding it in a forecast?
Why is ACF better than a simple Correl function before significance calculation\validation?
u&your site r great, thank you
(signifance validation=pval calculation)
See
https://stats.stackexchange.com/questions/263366/interpreting-seasonality-in-acf-and-pacf-plots
https://stats.stackexchange.com/questions/45191/interpreting-seasonality-with-acf-and-pacf
https://coolstatsblog.com/2013/08/11/how-to-use-autocorreation-function-acf-to-determine-seasonality/
Charles