Dickey-Fuller Test

We consider the stochastic process of form

image268z

where |φ| ≤ 1 and εi is white noise. If |φ| = 1, we have what is called a unit root. In particular, if φ = 1, we have a random walk (without drift), which is not stationary. In fact, if |φ| = 1, the process is not stationary, while if |φ| < 1, the process is stationary. We won’t consider the case where |φ| > 1 further since in this case the process is called explosive and increases over time.

This process is a first-order autoregressive process, AR(1), which we study in more detail in Autoregressive Processes. We will also see why such processes without a unit root are stationary and why the term “root” is used.

Basic Concepts

The Dickey-Fuller test is a way to determine whether the above process has a unit root. The approach used is quite straightforward. First calculate the first difference, i.e.

image269z

i.e.image270z

If we use the delta operator, defined by Δyi = yi – yi-1 and set β = φ – 1, then the equation becomes the linear regression equation

image271z

where β ≤ 0 and so the test for φ is transformed into a test that the slope parameter β = 0. Thus, we have a one-tailed test (since β can’t be positive) where

H0: β = 0 (equivalent to φ = 1)

H1: β < 0 (equivalent to φ < 1)

Under the alternative hypothesis, if b is the ordinary least squares (OLS) estimate of β, and so φ-bar = 1 + b is the OLS estimate of φ, then for large enough n

image272z

whereimage273z

We can use the usual linear regression approach, except that when the null hypothesis holds the t coefficient doesn’t follow a normal distribution and so we can’t use the usual t-test. Instead, this coefficient follows a tau distribution, and so our test consists of determining whether the tau statistic τ (which is equivalent to the usual t statistic) is less than τcrit based on a table of critical tau statistics values shown in Dickey-Fuller Table.

If the calculated tau value is less than the critical value in the table of critical values, then we have a significant result; otherwise, we accept the null hypothesis that there is a unit root and the time series is not stationary.

There are the following three versions of the Dickey-Fuller test:

Type 0 No constant, no trend Δyi = β1 yi-1 + εi
Type 1 Constant, no trend Δyi = β0 + β1 yi-1 + εi
Type 2 Constant and trend Δyi = β0 + β1 yi-1 + β2 i+ εi

Each version of the test uses a different set of critical values, as shown in the Dickey-Fuller Table. It is important to select the correct version of the test for the time series being analyzed. Note that the type 2 test assumes there is a constant term (which may be significantly equal to zero).

Example

Example 1: The net daily earnings of a small-time gambler are listed in column B of Figure 1. Use the Dickey-Fuller test to determine whether the times series is stationary.

We start by assuming that the correct model is type 1, namely constant but no trend.

Regression time series

Figure 1 – Regression on time-series data

Since we are using the regression model

image274z

(constant, no trend) we use the Real Statistics Linear Regression data analysis tool using range B4:B27 and the X data range and D5:D28 as the Y data range. Note that the values in column D are calculated by placing the formula =B5-B4 in cell D5, highlighting the range D5:D28 and pressing Ctrl-D.

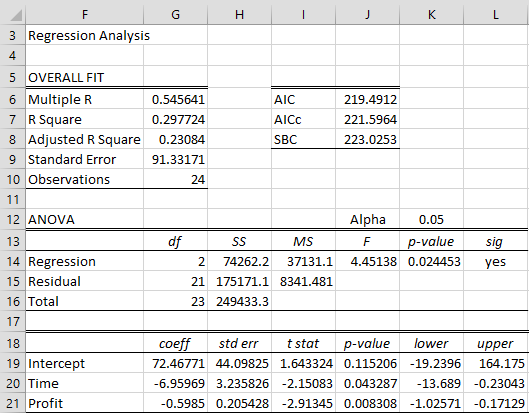
The output from the regression analysis is shown on the right side of Figure 1. In particular, we see that the t statistic (cell I20) for the β1 coefficient is -1.91613. This is the tau statistic. We now look up in the Dickey-Fuller Table, and find that the tau critical value for a type 1 test is -2.986 when n = 25 and α = .05. Since τcrit = -2.986 < – 1.91613 = τ, we cannot reject the null hypothesis that the time series is not stationary.

Note that the β1 coefficient (cell G20) is negative as expected. If instead, the coefficient were positive, then we would know that this type of Dickey-Fuller test was inappropriate since β1 = φ – 1 ≤ 0.

We now display in Figure 2 a plot of the time series values from Figure 1.

chart-dickey-fuller

Figure 2 – Chart of Winnings by Day

We see that there is an apparent downward trend towards the end of the 25 day period and so it is not surprising that the time series is not stationary. In fact, this leads us to choose the type 2 Dickey-Fuller test (with constant and trend). The result of this test is shown in Figure 3.

Dickey-Fuller with trend

Figure 3 – Dickey-Fuller with trend

Since we are using the regression model

Δyi = β0 + β1i + β2yi-1 + εi

this time, we use A4:B27 from Figure 1 as the X data range and D5:D28 as the Y data range. We see from Figure 3 that the t statistic (cell I21) for the β2 coefficient is -2.91345. We now look up in the Dickey-Fuller Table, and find that the tau critical value is -3.60269 for a type 2 test when n = 25 and α = .05. Since τcrit = -3.60269 < -2.91345 = τ, we cannot reject the null hypothesis that the time series is not stationary.

Worksheet Functions

Real Statistics Function: The Real Statistics Resource Pack provides the following array function where R1 contains a column of time series data.

ADFTEST(R1, lab, , , type, alpha): returns a 3 × 1 range which contains the following values: tau-statistic, tau-critical, yes/no (stationary or not)

If lab = TRUE (default is FALSE), the output consists of a 3 × 2 range whose first column contains labels. type = the test type (0, 1, 2, default is 1). The default value for alpha is .05.

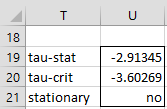
Note that for the type 2 test for Example 1, the output from the array formula

=ADFTEST(R6:R30,TRUE,,,2,U9)

agrees with the results we obtained above, as displayed in Figure 4.

adf-output

Figure 4 – Output from ADFTEST function

Note that the ADFTEST function can also be used to conduct the Augmented Dickey-Fuller test (ADF). See Augmented Dickey-Fuller Test. In fact, the ADFTEST function can take additional arguments and output other values, as explained on that webpage.

More functions

Real Statistics Functions: The Real Statistics Resource Pack provides the following functions

ADFCRIT(n, alpha, type) = critical value, tau-crit, for the stated type of ADF test at the stated alpha value, when the time series has n elements

ADFPROB(x, n, type) = estimated p-value (based on linear interpolation) for the ADF test at x

Thus for Example 1, we see that ADFCRIT(25,.05,2) = -3.60269.

Thus for Example 1, ADFCRIT(25,.05,2) = -3.60269. Also, ADFPROB(-2.91345,25,2) = “>.1”. ADFPROB takes values between .01 and .10; values greater than .1 are output as “>.1” and values less than .01 are output as “<.01”. Note that in the constant without trend case, if the tau-stat were -2.91345, then p-value = ADFPROB(-2.91345,25,1) = .060127.

Note that the ADFCRIT function will return critical values for alpha = .01, .025, .05 and .10 and for values of n found in the Dickey-Fuller Table as well as for values of alpha and n not included in the table.

Reference

Dickey, D. A., Fuller, W A. (1979) Distribution of the estimators for autoregressive time series with unit root. Journal of the American Statistical Association. Vol 74.
http://www.erudito.fea.usp.br/PortalFEA/Repositorio/537/Documentos/DIckey-Fuller%20(1981).pdf

34 thoughts on “Dickey-Fuller Test”

  1. Hello,
    That’s a fascinating text and very detailed, it helps a lot.
    I also would like to understand how to apply this method to check if two time series are co-integrated, two stocks for example. As I could understand from other lectures, the Dickey-Fuller test is a half of the work, we have to get the difference of the prices, but sometimes it is the regression, and sometimes it is the residual, I didn’t find a clear reference. If you could clarify, I would appreciate it very much. Maybe this could be a suggestion for another article.
    Thank you!

    Reply

  2. In this AR(1) example, to find the slope of the regression line, we can just use the calculation described in your “least-squares-method” article at https://www.real-statistics.com/regression/least-squares-method/. That means, the slope of the regression line (by using least-squares-method) is ONE number. And it’s either zero or none-zero. Why do we need to do hypothesis testing for it? For ex, in https://www.real-statistics.com/regression/least-squares-method/, the slope is -0.62. So -0.62 not zero. Then we can simply reject the hypothesis. Isn’t it? Or, we need to to do hypothesis testing because the least-squares-method is just an estimate?

    Reply

    • Hi PJ,
      The slope calculated by the least-square method is based on the sample. If the slope id -.62, then clearly, the slope based on the sample is not zero. But this is not what hypothesis testing is about. Hypothesis testing concerns the real (i.e. population) slope, which is only being estimated via the sample. The real slope might still be zero, and the testing is related to the likelihood that this value is zero even though the slope calculated based on the sample is -.62.
      Charles

      Reply

  4. Hi,

    you wrote that under the null hypothesis the t-coefficient follows a tau distribution but in several papers I read that the distribution of the test statistic is defined in terms of integrals of Brownian motions. This point is not clear to me.

    thanks!

    Reply

  5. “the t statistic (cell I19) for the β1 coefficient is -1.91613”

    This references either wrong the cell or the wrong value. The cell I20 = -1.91613, whereas I19 = -0.66906.

    Please can you clarify and/or correct the text.

    Reply

    • FJD,
      Thanks for bringing this error to my attention. The reference should be to cell I20. O have now changed the text.
      I appreciate your help in improving the accuracy of the website.
      Charles

      Reply

  6. if the sample i have is less than 25 observations, can I still be using this ? what about the table? the values in it only starts with n=25
    thank you

    Reply

  7. Very nice explanation sir. But I have a doubt sir. In the type 1 assumption, we cannot reject H0 as Critical value has(-2.985 < – 1.91613) and we also have a p=0.068. Quite ok. But in the type 2 assumption , τcrit = -3.60269 < -2.15083 = τ but p=0.008. This is where I am a little bit concerned sir. Don't we see this p as a significant one generally.
    Kindly clarify sir.

    Reply

  8. Hi, in your excel example DF0, DF1, DF2 page, why tau is depend on t stat? and when I use real statistic to do ADF Test, I always print DF0 result, I want print DF1 and DF2 result, what I should do? Thanks!

    Reply

    • Hello Chen,
      1. As described on this webpage, the test is equivalent to determining whether the slope coefficient in the Δy_i = β * y_i-1 + ε_i regression is zero. This is a t test.
      2. DF0 is the case where there is no constant or trend, DF1 is the case where there is a constant but no trend and DF2 is the case where there is a constant and a trend. The Real Statistics ADF test gives you these three options.
      Charles

      Reply

  9. Hi,
    In the example of the type 2 test, what is the difference in interpretation between the tau statistic for profit and for time? Why did you analyze the time t stat instead of the profit t stat?
    Thank you so much!

    Reply

      • I believe Sarah was asking which T-stat we should be looking in the the type 2 test? Profit or Time?

        “We see from Figure 3 that the t statistic (cell I21) for the coefficient is -2.15083.”

        The confusion may come from the text referring to cell I21 (profit T-stat), but the t statistic -2.15083 is from cell I20 (time T-stat).

        Reply

  10. To reject the H0, should you look at the p-value or should you compare the two t-values for the Dickey Fuller test?

    Reply

  11. There are three different types of the DF test described where the difference between the Type 0 (No constant, no trend) and the Type 1 (Constant, no trend) is that the latter includes an intercept β0. This is why I don’t understand why in Example 1 the question whether the time series is stationary is judged by looking at the β1 coefficient from figure 1. Same is true for the text about figure 3. So do we always judge by the β1 coefficient if a time series is stationary?

    Reply

  13. Hi is there any chance to get the full spreadsheet? the bit you explain how to use function ADFTEST refers to column U and I am not sure what parameters to use here.

    Thanks!

    Reply

Leave a Comment