Real Statistics Data Analysis Tool: The Real Statistics Resource Pack provides the Correlogram data analysis tool which outputs an ACF or PACF correlogram that includes the confidence intervals.
ACF Correlogram
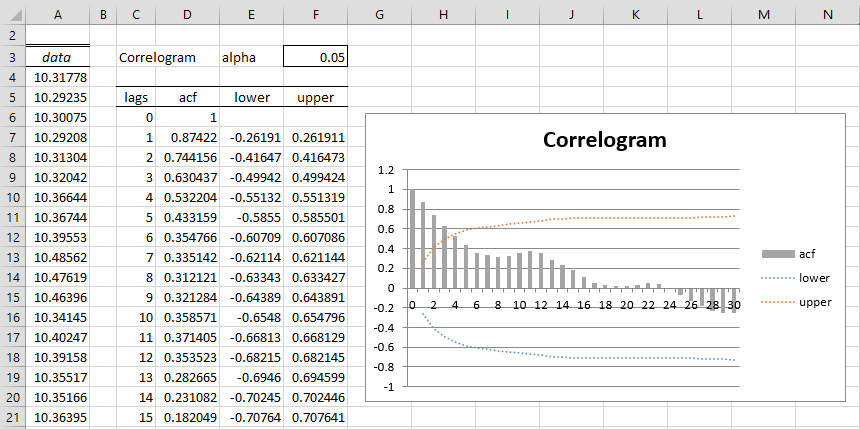
Example 1: Construct an ACF Correlogram for the data in column A of Figure 1 (only the first 18 of 56 data elements are visible).
Figure 1 – ACF Correlogram
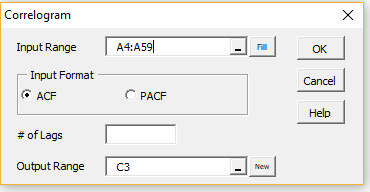
Press Ctr-m and choose the Time Series option (or the Time S tab if using the Multipage interface). Select the Correlogram option and click on the OK button. Now, fill in the dialog box that appears as shown in Figure 2. Since the # of Lags field was left blank, the default of 30 was used.
Figure 2 – Correlogram dialog box
After clicking on the OK button, the output shown on the right side of Figure 1 appears. Note that the alpha value in cell F3 is automatically set to .05. You can change this to any value you like between 0 and 0.5 and all the cells as well as the chart will change to reflect your choice for alpha.
Note that cell D7 contains the formula =ACF($A$4:$A$59,C7), cell E7 contains the formula =-F7 and cell F7 contains the formula
=NORM.S.INV(1-$F$3/2)/SQRT(COUNT($A$4:$A$59))
The remaining values in columns D and E (until row 36, corresponding to lag 30) are calculated using similar formulas. Cell F8 contains the formula
=NORM.S.INV(1-$F$3/2)*SQRT((1+2*SUMSQ(D$7:D7))/COUNT($A$4:$A$59))
and similarly, for the other cells in column F. This reflects the fact that the standard error and confidence interval of ACF(k) are
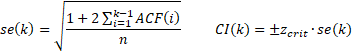
PACF Correlogram
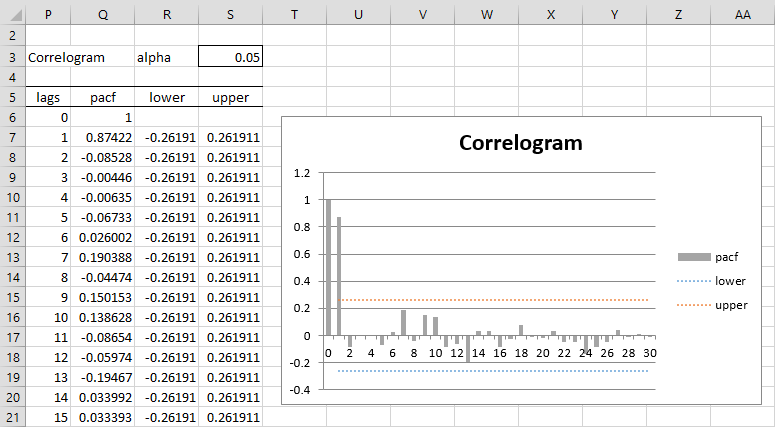
Example 2: Construct a PACF Correlogram for the data in column A of Figure 1.
This time the PACF option from the dialog box in Figure 2 is selected. The output is shown in Figure 3 (only the firsts 15 of 30 lags is shown).
Figure 3 – PACF Correlogram
Cell Q7 contains the formula =PACF($A$4:$A$59,P7), cell R7 contains =-S7 and cell S7 contains =NORM.S.INV(1-$S$3/2)/SQRT(COUNT(A4:A59)). This reflects the fact that the standard error and confidence interval of PACF(k) are
