ARIMA models
As described in ARMA Models, an ARMA(p,q) model can be expressed as
If φ0 = 0 (i.e. the mean of the stochastic process is zero) then this can be expressed using the lag operator as
Note too that an ARIMA(p, d, q) process zi can be expressed as above but first zi must be replaced by zi = yi – yi-d. Alternatively, we can express an ARIMA(p, d, q) process yi without constant as
We can add the constant term back in as
![]()
Seasonal ARIMA
A seasonal ARIMA model takes the same form, but now there are additional terms that reflect the seasonality part of the model. Specifically, a SARIMA(p,d,q) × (P,D,Q)m model without constant can be expressed as
where
![]()
Here, we have P seasonal autoregressive terms (with coefficients Φ1, …, ΦP), Q seasonal moving average terms (with coefficients Θ1, …, ΘQ) and D seasonal differencing based on m seasonal periods.
Let’s assume that the two types of differencing (corresponding to d and D) have already been done. Then a SARIMA(1,0,1) × (1,0,1)12 model takes the following form:
![]()
![]()
![]()
The residuals can therefore be expressed as:
The forecast can be expressed (where the coefficients should have a hat on them):
![]()
Similarly, a SARMA(p,q) × (P,Q)m model without constant can be expressed as
And so
![]()
which is equivalent to
![]()
In the case where there is a constant term φ0 this expression takes the form
![]()
This serves as the equation to estimate the forecast at time i (when the final εi is set to zero). You can also solve for εi to obtain an expression that can be used to estimate the residuals.
References
Greene, W. H. (2002) Econometric analysis. 5th Ed. Prentice-Hall
https://www.ctanujit.org/uploads/2/5/3/9/25393293/_econometric_analysis_by_greence.pdf
Gujarati, D. & Porter, D. (2009) Basic econometrics. 5th Ed. McGraw Hill
http://www.uop.edu.pk/ocontents/gujarati_book.pdf
Hamilton, J. D. (1994) Time series analysis. Princeton University Press
https://press.princeton.edu/books/hardcover/9780691042893/time-series-analysis
Wooldridge, J. M. (2009) Introductory econometrics, a modern approach. 5th Ed. South-Western, Cegage Learning
https://cbpbu.ac.in/userfiles/file/2020/STUDY_MAT/ECO/2.pdf
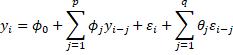
Hi, I would like to use your mathematical expression of SARIMA in my PhD thesis and I was wondering if you could provide me with the source you would like me to use. I want to make sure I reference it correctly.
Hello John,
See https://real-statistics.com/appendix/citation-real-statistics-software-website/
Charles