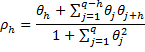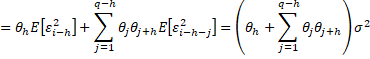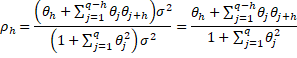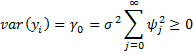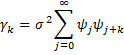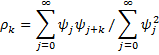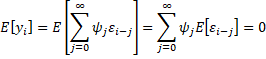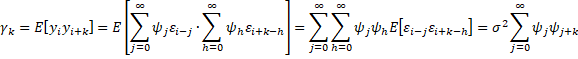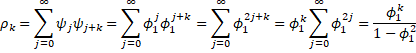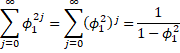Moving Average Basic Concepts
The following are proofs of properties found in Moving Averages Basic Concepts
Property 1: The mean of an MA(q) process is μ.
Proof:
Property 2: The variance of an MA(q) process is
Proof:
Property 3: The autocorrelation function of an MA(1) process is
Proof:
When h = 1
since E[εi-1] = 0. When h > 1
Thus for h = 1, by Property 2
and for h > 1
Property 4: The autocorrelation function of an MA(2) process is
Proof:
Thus, when h = 1
and when h = 2
and when h > 2
It now follows that for h = 1, by Property 2
and for h = 2
and for h > 2
Property 5: The autocorrelation function of an MA(q) process is
for h ≤ q and ρh = 0 for h > q.
Proof: As in the proof of Property 3 of Autoregressive Processes, it is sufficient to prove the property in the case where the mean = 0 (and so the constant term is zero). Since E[εiεi] = σ2 and E[εiεi-j] = 0 when j > 1, it follows that
for h ≤ q and cov(yi, yi-h) = 0 if h > q.
By Property 2 it now follows that
for h ≤ q and ρh = 0 for h > q.
Infinite Moving Average Processes
The following is a proof of Property 4 in Infinite Moving Average Processes.
Property 4: The following are true for any MA(∞) process
Proof: The assumption that the infinite sum of the absolute values of the ψi terms is finite is needed to show that all the infinite series listed below converge. As usual, it is sufficient to demonstrate the above properties in the case where the mean is 0.
since E[εi-jεi+k-h] = σ2 if h = j+k and zero otherwise.
The other two properties follow from this last one.
Observation: Property 4 can be used to provide an alternative proof of various properties of AR(p) processes. For example, for an AR(1) process we have seen that ψj = φ1j, and so
This last equality results from the fact that |φ1| < 1, and so φ12 < 1, in which case we have a geometric series that converges as follows:
See Geometric Series for a proof that the geometric series converges.