MA(q) Process Basic Concepts

Introduction

A q-order moving average process, denoted MA(q), takes the form

MA(q) process

Thinking of the subscripts i as representing time, we see that the value of y at time i is a linear function of past errors. We assume that the error terms are independently distributed with a normal distribution with mean zero and a constant variance σ2. Thus

εi ∼ N(0, σ2)          cov(εi, εj) = 0 if i ≠ j

An MA(q) process can also be expressed as

image138z

where zi = yi – μ. Thus, we can often simplify our analyses by restricting ourselves to the case where the mean is zero.

Using the lag operator, we can express a zero mean MA(q) process as

image139z

whereimage140z

Mean and variance

Property 1: The mean of an MA(q) process is μ.

Property 2: The variance of an MA(q) process is

image141z

Autocorrelation

Property 3: The autocorrelation function of an MA(1) process is

image142z

Property 4: The autocorrelation function of an MA(2) process is

MA(2) ACF

We now generalize these properties to all MA(q).

Property 5: The autocorrelation function of an MA(q) process is

image144z

for h ≤ q and ρh = 0 for h > q

Observation: The proofs of Property 1 – 5 are given in Moving Average Proofs.

Property 6: The PACF of an MA(1) process is

image145z

where 1 ≤ j < n.

If the process is invertible (see Invertible MA(q) Processes) then

image146z

MA(1) Example

Example 1: Simulate a sample of size 199 from the MA(1) process yi = 4 + εi + .5εi-1 where εi ∼ N(0,2).

Thus μ = 4, θ1 = .5 and σ = 2. We simulate the independent εi by using the Excel formula =NORM.INV(RAND(),0,2) in column B of Figure 1 (only the first 20 of 199 values is shown). The yi values are calculated by placing the formula =4+B5+0.5*B4 in cell C5, highlighting the range C5:C203 and pressing Ctrl-D. The graph of the y values is shown on the right side of Figure 1. As you can see, no particular pattern is visible.

Simulated MA(1) process

Figure 1 – Simulated MA(1) data

By Properties 1 and 2, the theoretical values for the mean and variance are μ = 4 and var(yi) = σ2(1+\theta_1^2) = 22(1+.52) = 5. These compare to the actual time series values of y̅ = AVERAGE(C6:C204) = 4.358 and s2 = VAR.P(C6:C204) = 4.401.

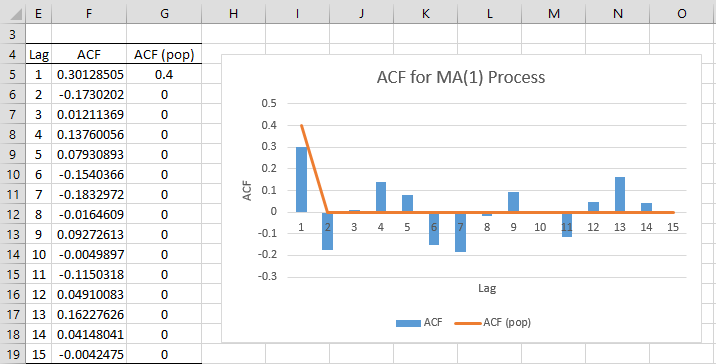
The ACF values are shown for lags 1 through 15 in Figure 2. These are calculated from the y values as in Example 1 of AR(p) Process Basic Concepts. Note that the ACF value at lag 1 is .301285. Based on Property 3, the population ACF value at lag 1 is

image147z

MA(1) ACF

The ACF values for lags h > 1 vary from about -.18 to .16, compared to the theoretical value of ρh = 0 (per Property 3). As you can see from Figure 2, the sample values can be quite different from the theoretical values.

MA(1) ACF

Figure 2 – ACF for MA(1) process

Observation: By Property 3

image142z

But note that

image148z

and so the reciprocal of θ1 yields the same ACF. Thus, if we are seeking a coefficient θ1 that yields a particular ρ1 value, we can always choose a coefficient whose absolute value is at most 1. In fact, it turns out that there is always a unique such θ1 whose absolute value is less than 1.

This is also true for any MA(q) process, and so we will restrict our MA(q) processes to those where |θj| < 1 for all j. This also ensures that the MA(q) process is invertible (see Invertible MA(q) Processes).

MA(1) PACF

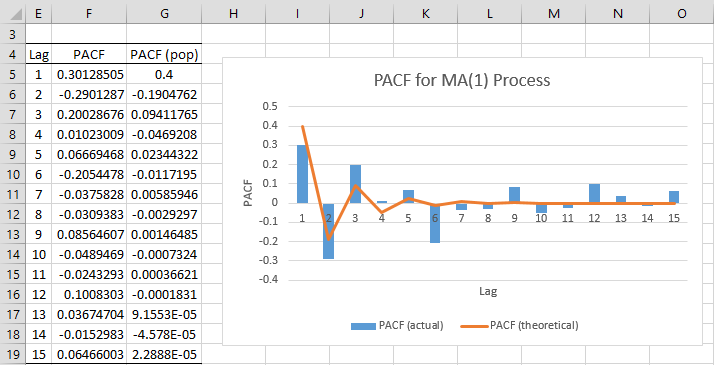
Example 2: Chart PACF for the data in Example 1.

The approach is as described in Example 1 of Partial Autocorrelation Function. The chart is shown in Figure 3.

PACF for MA(1)

Figure 3 – Graph of PACF for MA(1) Process

The theoretical PACF values are calculated using Property 6. In particular, we insert the following formula in cell G5, highlight the range G5:G19 and press Ctrl-D.

=-((-0.5)^E5*(1-0.5^2)/(1-0.5^(2*E5+2)))

Note that we couldn’t use the following formula

=-(-0.5)^E5*(1-0.5^2)/(1-0.5^(2*E5+2))

This is because Excel incorrectly evaluates any expressions of the form -a^n as if they were (-a)^n. Thus –1^2 and –(–1)^2 are evaluated as 1 instead of -1.

Observation: We can see from Figure 3 that the absolute value of the PACF values tends towards zero as the lag increases. This is generally true for an MA(q) model.

References

Greene, W. H. (2002) Econometric analysis. 5th Ed. Prentice-Hall
https://www.scirp.org/(S(351jmbntvnsjt1aadkposzje))/reference/referencespapers.aspx?referenceid=1243286

Gujarati, D. & Porter, D. (2009) Basic econometrics. 5th Ed. McGraw Hill
http://www.uop.edu.pk/ocontents/gujarati_book.pdf

Hamilton, J. D. (1994) Time series analysis. Princeton University Press
https://press.princeton.edu/books/hardcover/9780691042893/time-series-analysis

Wooldridge, J. M. (2009) Introductory econometrics, a modern approach. 5th Ed. South-Western, Cegage Learning
https://cbpbu.ac.in/userfiles/file/2020/STUDY_MAT/ECO/2.pdf

Wei, W. (2006) Time series analysis: univariate and multivariate methods, 2nd edition. Pearson Addison Wesley https://www.researchgate.net/publication/236651810_Time_Series_Analysis_Univariate_and_Multivariate_Methods_2nd_edition_2006

12 thoughts on “MA(q) Process Basic Concepts”

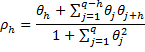
  1. Again we thank you for the valuable informations ….Our question are:
    You are using :
    1- yi = 4 + εi + .5εi-1 how it is obtained is it an initial assumption
    2- μ = 4 while MA by definition use error with mean=0
    3- εi is obtained using the Excel formula =NORM.INV(RAND(),0,2) why not: e = y – y(cap)
    4- If we have time and measured (y) data (or R-datad) in 2-columons may you give example to forecast the future (y) and Give is metrics

    Reply

  3. Dear Charles

    I have a question.
    For the practical forecasting, what is exactly “residual” in the future?
    I mean, when I’m using MA(1) model to forecast t+2, then I should have “residual” of t+1.
    But “residual” is the difference between my forecast and actual data, isn’t it?

    Reply

    • Yes, the “residual” is the difference between your forecast and the actual data.
      I don’t see where there is a reference to a residual for a future time on this webpage.
      Charles

      Reply

      • Dear Charles

        Thank you for your answer. I thought my question is about the basic concept so that’s why I’m asking here.

        So let me return to my question.
        When I make a MA(1) model for monthly stat, how can I make forecast of t+2 future? I mean, I don’t have actual value of t+1, so I can’t calculate residual of t+1. So I’m wondering how can I expand this model to longer future.

        Reply

        • The forecast at t+2 is based on the data at times 1,…,t and not t+1. You can’t calculate residuals since you don’t know the observed value at t+2, but you can calculate the standard error of the forecast (and therefore the confidence interval of the forecast).
          AS you can imagine, the standard error for t+2 is larger than that at t+1 and the standard error at t+3 is larger than at t+2, etc.
          Charles

          Reply

  4. All of this material is so good! I was wondering, why did you start with:

    yi = 4 + εi + .5εi-1

    I cannot seem to determine who that was calculated. Was it from another data set?
    Thank you

    Reply

    • Hello Dean,
      This was just a way to generate an MA(q) time series with known properties. The time series is in column C (based on the residuals in column B). We can now look at the resulting MA(q) model and see how close the coefficients are to those in yi = 4 + εi + .5εi-1.
      Charles

      Reply

Leave a Comment