Introduction
If we know (or assume) that a time series can be fit by an MA(q) process, then we need to figure out the value of the parameters μ, σ2, q, θ1, …, θq.
The initial approach to determining the value for q is to look at the ACF values for the time series under consideration. Since we know that for an MA(q) process, ρk = 0 for all k > q, we seek the first value for q where ACF(q) is approximately zero. We will refine this approach in Comparing ARIMA Models.
We next turn our attention to finding the other parameters that provide the best fit for the data.
MA(1) Properties
We start by looking at an MA(1) process yi = μ + εi + θ1εi-1 .
We estimnate the mean and variance as follows.
Property 1: The mean is μ.
Property 2: The variance is
![]()
We estimate the autocorrelation function as follows.
Property 3: The autocorrelation function is
![]()
We start by using the mean of the time series as μ. We then subtract this value from all the time series values to get a zero mean time series. Next, we calculate the variance s2 and r = ACF(1) of the time series. Finally, we can solve for θ1 using the equation
which is equivalent to the quadratic equation
Actually θ1 above is really the estimated value of θ1 which typically has a hat over it. These solutions are real provided |r| < .5. It turns out that for large values of n
Example
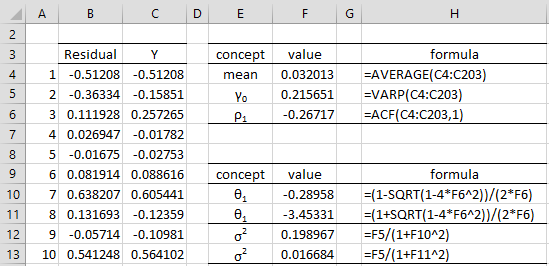
Example 1: Assuming that the time series in range C4:C203 of Figure 1 fits an MA(1) process (only the first 10 of 200 values are shown), find the values of μ, σ2, θ1 for the MA(1) process.
We actually created the time series using the MA(1) process yi = εi – .4εi-1 with σ2 = .25. Thus, we entered the formula =NORM.INV(RAND(),0,.5) in all the cells in range B4:B203 and placed the formula =B4 in cell C4 and the formula =B5-.4*B4 in cell C5. We then highlighted range C5:C203 and pressed Ctrl-D.
Figure 1 – Calculating MA(1) parameters
We now calculate the mean (cell F4), variance (cell F5) and autocorrelation from the time series as shown in the upper right-hand side of Figure 1. From these values, we calculate two possible values for θ1, namely -0.28958 and -3.45331. Note that these values are reciprocals of one another. Only the value θ1 = -0.28958 yields an invertible MA(1) process since |θ1| < 1. In this case, we see that σ2 = 0.198967.
The result is an estimate of the MA(1) process, namely
with an estimate of 0.198967 for the variance of the εi. Using a one-sample t-test, we can see that the mean is not significantly different from zero (t = .97, p-value = .33, 2 tailed test).
Confidence Interval
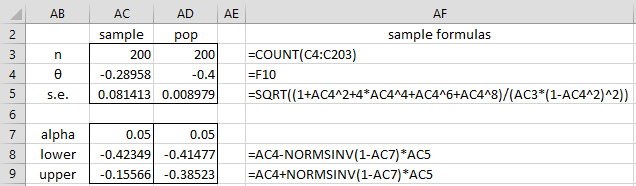
We can compute a somewhat crude 95% confidence range for θ1 based on the normal approximation, as shown in Figure 2.
Figure 2 – Confidence interval
If we knew the real value of θ1 the confidence interval would be as shown in column AD of Figure 2. Since we don’t know the actual value of θ1 we have to make do with the values estimated in Figure 1 when calculating the standard error (as shown in column AC of Figure 2). Thus, we see that the real value lies in the interval (-.42349, -.15566) with 95% confidence.
Observation: In the above example we used a sample with 200 elements. When we repeated the same analysis with a sample of 1,000 elements we got the following estimates, which are closer to the original MA(1) process parameters:
with σ2 = 0.23683. The 95% confidence interval for θ1 also narrowed to (-.446, -.311).
We can obtain better estimates using other techniques, as shown in Calculating MA(q) Coefficients using Solver.
Estimate of σ2
When using the method of moments approach to estimating the MA(q) coefficients, we can estimate the variance of the error terms via the following formula:
where s2 is the variance for the time series
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Greene, W. H. (2002) Econometric analysis. 5th Ed. Prentice-Hall
https://www.ctanujit.org/uploads/2/5/3/9/25393293/_econometric_analysis_by_greence.pdf
Gujarati, D. & Porter, D. (2009) Basic econometrics. 5th Ed. McGraw Hill
http://www.uop.edu.pk/ocontents/gujarati_book.pdf
Hamilton, J. D. (1994) Time series analysis. Princeton University Press
https://press.princeton.edu/books/hardcover/9780691042893/time-series-analysis
Wooldridge, J. M. (2009) Introductory econometrics, a modern approach. 5th Ed. South-Western, Cegage Learning
https://cbpbu.ac.in/userfiles/file/2020/STUDY_MAT/ECO/2.pdf
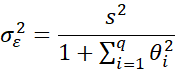
you calculate two different values for θ1, namely -0.28958 and -3.45331 with the same equation ,and how these values are reciprocals of one another.
you started example 1 by the equation yi = εi – .4εi-1 with σ2 = .25. without how you obtained them or are they assumed…Is this obtained by regression of measured data (y)
You used the residual with formula =NORM.INV(RAND(),0,.5) and it will be more clear why you did not use :e= y -y (cap)
Hassan,
See my previous response.
Charles
Hi Charles,
how to determine the MA Coefficient if ACF > 0.5?
Hi Charles,
Thanks for putting together this content. I recently started learning Time Series Analysis. I am thinking to build an MA model from scratch in Python. But I am stuck at calculating the error term. In your examples, you are randomly generating the residuals. But in real-world applications how to calculate the error term/residual given the time series data?
Thanks
Hi ,
I am randomly generating residuals in order to generate the appropriate type of time series. This is only for educational purposes. The procedure described works with any time series and calculates the estimated residuals.
Charles
If i would like to forecast power load using MA(1) process
yi = μ + εi + θ1εi-1
and I generate the error terms using =NORM.INV(RAND(),0,.σ) and μ is the mean of my real data. Each time I opened the computer, or I compute it using a different computer, the random error will be different and hence the forecasted results will be different. So in this case the forecasted results using MA, ARMA and ARIMA will not be standard answers???
I only used RAND() to create the data set, not to calculate the coefficients or forecast results.
Charles
Dear Charles, I do have a question and hope you can help to answer.
In forming the quadratic equation for theta1 you mentioned real solutions are possible only if |r| 0.5 then?
Kind regards,
Chee Wee