Basic Concepts
Just as we can define an infinite-order moving average process, we can also define an infinite-order autoregressive process, AR(∞). It turns out that any stationary MA(q) process can be expressed as an AR(∞) process. E.g. suppose we have an MA(1) process with μ = 0.
Thus
Continuing in this way, after n steps we have
As a result, we have
Or equivalently
It turns out that if |θ1| < 1 then this infinite series converges to a finite value. Such MA(q) processes are called invertible.
Properties
Property 1: If |θ1| < 1 then the MA(1) process is invertible
Property 2: The MA(q) process yi = μ + εi + θ1εi-1 + ⋅⋅⋅ + θqεi-q is invertible provided the absolute value of all the roots of the characteristic polynomial 1 + θ1L + θ1L2 + ⋅⋅⋅ + θqLq = 0 is greater than 1.
Worksheet Function
Real Statistics Function: The Real Statistics Resource Pack supplies the following array function where R1 is a q×1 range containing the theta coefficients of the polynomial where θq is in the first position and θ1 is in the last position.
MARoots(R1): returns a q × 3 range where each row contains one root, and where the first column consists of the real part of the roots, the second column consists of the imaginary part of the roots and the third column contains the absolute value of the roots
This function uses the ROOTS function described in Roots of a Polynomial. Note that just like in the ROOTS functions, the MARoots function can take the following optional arguments:
MARoots(R1, prec, iter, r, s)
prec = the precision of the result, i.e. how close to zero is acceptable. This value defaults to 0.00000001.
iter = the maximum number of iterations performed when performing Bairstow’s Method. The default is 50.
r, s = the initial seed values when using Bairstow’s Method. These default to zero.
Example
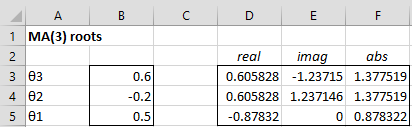
Example 1: Determine whether the following MA(3) process is invertible
yi = 4 + εi + .5εi-1 – .2εi-2 + .6εi–3
We insert the array formula =MARoots(B3:B5) in range D3:F5 to obtain the results shown in Figure 1.
Figure 1 – Roots of an MA(3) process
We see that the three roots of the characteristic equation are -.605828–1.23715i, -.605828+1.23715i, and -0.87832. Since the absolute value of the real root is less than 1, we conclude that the process is not invertible.
Example 2: Determine whether the following MA(2) process is invertible
yi = εi – .1εi-1 + .21εi-2
Using the same approach as for Example 1, we see that the roots of the characteristic polynomial are 10/3 and 10/7, both of which are greater than one. Thus, we conclude that this is an invertible process.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Peiris, M. S. (2013) Invertibility of MA processes. Time series concepts & methods
https://talus.maths.usyd.edu.au/u/UG/SM/STAT3011/r/TS/NOTES10.pdf
Brockwell, P. J. and Davis, R. A. (2002) Introduction to time series and forecasting, 2nd Ed. Springer.
http://home.iitj.ac.in/~parmod/document/introduction%20time%20series.pdf
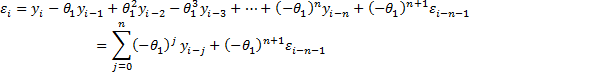
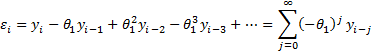
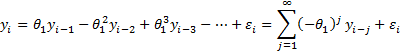
very helpful material sir. I was just confused about the examples of invertible and non-invertible processes. i mean if u can guide me with examples of both.
thanks
Hello Usman,
Sorry for the delayed response. An MA(q) process is invertible when the absolute values of all the roots of the characteristic equation, as defined on this webpage, are larger than 1. Thus the process in Example is not invertible (since .878322 <= 1). But y_i = e_i - 1*e_i-1 + .21*e_i-2 is invertible since both roots (10/3 and 10/7) are greater than 1. Charles
please guide me to check the invertibility of following ma processes
process 1: yt = zt+0.2zt-1
process 2:yt=0.6zt +0.7 zt-1+0.1zt-2
The approach for checking invertibility is described on the wbepage. You just need to carry out the steps listed.
Do you have a specific question?
Charles
How can the invertibility of process 2 from saadwaseem be checked? Since zt does have a 0.6 (not 1) coefficient, the process does not follow the form yt = zt + theta1z_{t-1} + theta2z_{t-2}.
Otto,
To be an MA process the coefficient for z_t must be 1 (where z is epsilon). This can be done by dividing both sides of the equation by .6 to obtain
y_t/.6 = z_t + 7/6*z_t – 1/6*z_t-2. You now need to define w_t = y_t/.6, and so the MA(2) process is u_t = z_t + 7/6*z_t – 1/6*z_t-2.
The root for theta1 is 7.772 and the root for theta2 is .772. I hope that I haven’t made an error in these calculations.
Charles
A recent comment by Otto makes me aware that my reply to you was not complete. I replicate my reply to Otto as follows.
To be an MA process the coefficient for z_t must be 1 (where z is epsilon). This can be done by dividing both sides of the equation by .6 to obtain y_t/.6 = z_t + 7/6*z_t – 1/6*z_t-2. You now need to define w_t = y_t/.6, and so the MA(2) process is u_t = z_t + 7/6*z_t – 1/6*z_t-2.
The root for theta1 is 7.772 and the root for theta2 is .772. I hope that I haven’t made an error in these calculations.
Charles
Hello Charles,
If there are 2 candidate MA(q) models (with the same value) of q and with the same ACF plot, it is said the invertible model should be chosen over the non-invertible model. Is there any intuition why the invertible model will produce better forecasts?
See https://stats.stackexchange.com/questions/333802/why-do-we-care-if-an-ma-process-is-invertible
Charles
Thanks for pointing in the right direction 🙂
Hello Charles,
I am trying to see that in ar(infinity) process the covariance between yt and yt-2 is equal to zero. I know that it is in MA(1) process but I am not able to do the math in ar(infinity).
Can you advise on this?
Hello Yelda,
I have not tried to do the calculation in an AR(infinity) model, but I do know that since it is equivalent to an MA model, it is easier to derive the result there.
Charles
Yelda,
I have just added some proofs of AR(1) properties using MA(infinity). This might help you in deriving a MA(1) proof using AR(infinity). See the following webpage (esp. the Observation at the end) Moving Average Proofs.
Charles