Basic Concepts
An infinite-order moving average process, denoted MA(∞), takes the form
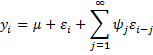
where the following infinite sum is finite (i.e. converges to a real value)
and
εi ∼ N(0, σ2) cov(εi, εj) = 0 if i ≠ j
We can also express an MA(∞) process as 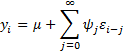
where it is assumed that ψ0 = 1.
Observation: That |ψj|converges ensures that the yi take finite values and that
converges.
AR(1) Process
Example 1
Show that the AR(1) process from Example 1 of Autoregressive Processes Basic Concepts can be represented by an MA(∞) process.
By Property 1 of Autoregressive Processes Basic Concepts
Then the original AR(1) process can be transformed into the process
which results in
Continuing in this way, we get
which is the desired MA(∞) process.
Property 1
Any stationary AR(1) process can be expressed as an MA(∞) process. In fact
Proof: Using the same approach as in Example 1, we find that the AR(1) process
Since the original process is a stationary AR(1), |φ1| < 1 and the εi have the desired properties.
Observation
Another way to see this is to use the lag operator, namely that an AR(1) process (with zero mean) can be expressed as
Substituting the first equation inside the second, we get
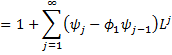 Here we recall that φ0 = 1. Equating the coefficients, we see that for all j > 0
Here we recall that φ0 = 1. Equating the coefficients, we see that for all j > 0
Thus
![]()
and so ψ(L) is the inverse of φ(L)![]()
AR(p) and MA(∞) equivalence
Property 2: Any stationary AR(p) process can be expressed as an MA(∞) process.
Proof: The proof is similar to that of Property 1.
AR(2) Example
Example 2: Show that the following AR(2) process can be represented by an MA(∞) process.
By Property 1 of Autoregressive Processes Basic Concepts, the mean is
Then the original AR(2) process can be transformed into the process
etc. Thus the first few terms of the MA(∞) process are
![]()
Key Properties
Property 3 (Wold’s Decomposition Theorem): Any stationary process can be represented as an MA(∞) process
Property 4: The following are true for any MA(∞) process
Proof: See Moving Average Proofs
Worksheet Function
Real Statistics Function: The Real Statistics Resource Pack provides the following array function where R1 is a column range consisting of phi coefficients and R2 is a column range consisting of theta coefficients.
PSICoeff(R1, R2, k, rev): returns a k × 1 range containing the first k psi coefficients (starting with ψ0 = 1) for the ARMA model with the coefficients in R1 and R2.
If k is omitted (default) then k is set equal to the number of rows in the highlighted range. If rev = TRUE (default), then the phi and theta coefficients are listed in reverse order φp, φp-1, …, φ1 and order θq, θq-1, …, θ1.
Since both phi and theta coefficients can be present, this function can also handle ARMA processes as described in ARMA Processes.
We can use the PSICoeff function to find the psi coefficients for Example 2 as shown in range I10:I14 of Figure 1.
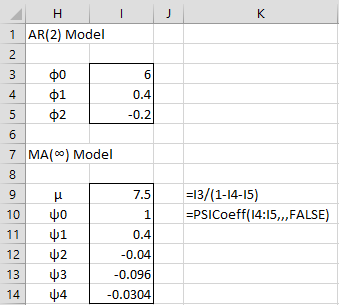
Figure 1 – Convert AR(2) model into an MA(∞) model
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Greene, W. H. (2002) Econometric analysis. 5th Ed. Prentice-Hall
https://www.ctanujit.org/uploads/2/5/3/9/25393293/_econometric_analysis_by_greence.pdf
Gujarati, D. & Porter, D. (2009) Basic econometrics. 5th Ed. McGraw Hill
http://www.uop.edu.pk/ocontents/gujarati_book.pdf
Hamilton, J. D. (1994) Time series analysis. Princeton University Press
https://press.princeton.edu/books/hardcover/9780691042893/time-series-analysis
Wooldridge, J. M. (2009) Introductory econometrics, a modern approach. 5th Ed. South-Western, Cegage Learning
https://cbpbu.ac.in/userfiles/file/2020/STUDY_MAT/ECO/2.pdf
Wei, W. (2006) Time series analysis: univariate and multivariate methods, 2nd edition. Pearson Addison Wesley https://www.researchgate.net/publication/236651810_Time_Series_Analysis_Univariate_and_Multivariate_Methods_2nd_edition_2006
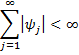
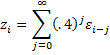
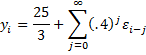
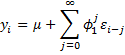
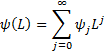
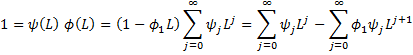
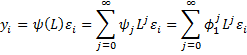
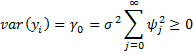
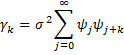
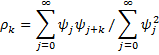
How can I calculate the covariance and autocorrelation of infinite moving average process
Ligawa,
Sorry, but I don’t know the answer to your question.
Charles
if y(t)=e(t)+5 e(t-1)+10e(t-2), e(t)~N(0,16), what’s the inverse of that MA model?
Hello Assma,
See the following webpage about the inverse of an MA(q) model.
https://www.real-statistics.com/time-series-analysis/moving-average-processes/invertibility-ma-processes/
Charles
Very resourceful and useful to me. Thank you