We use the following terminology: if y1, …, yn represents a time series, then ŷi represents the ith forecasted value, where i ≤ n. For i ≤ n, the ith error ei (aka residual) is then
Our goal is to find a forecast that minimizes the errors.
Key measures
A number of measures are commonly used to determine the accuracy of a forecast. These include the mean absolute error (MAE), mean squared error (MSE) and root mean squared error (RMSE).
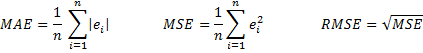
Note that MAE is also commonly called mean absolute deviation (MAD). This version of MAD should not be confused with the median absolute deviation (MAD) described in Measures of Variability.
Other measures
Some other measurements are mean absolute percentage error (MAPE), mean absolute scaled error (MASE) and symmetric mean absolute percentage error (SMAPE).
For data with seasonality (see Holt-Winter Forecasting) where the periodicity is c, the formula for MASE becomes
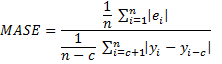
Theil statistics
Finally, there is Theil’s U statistic, which is computed by the formula
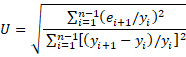
If U < 1, the forecasting technique is better than guessing. If U = 1 then the forecasting technique is as good as guessing. If U > 1 then the forecasting technique is worse than guessing.
Actually, U is also called Theil’s U2 statistic. There is also a less-often used U1 statistic
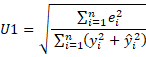 U1 takes values between 0 and 1, with values nearer to 0 representing greater forecast accuracy.
U1 takes values between 0 and 1, with values nearer to 0 representing greater forecast accuracy.
Real Statistic Support
Click here for information about Real Statistics support for the forecast error measures described on this webpage.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage
References
Hyndman, R. J. and Athanasopoulos, G. (2018) Evaluating forecast accuracy. Forecasting: Principles and Practice. 2nd ed.
https://otexts.com/fpp2/accuracy.html
Oracle (2018) Time-series forecasting error measures
https://docs.oracle.com/en/cloud/saas/planning-budgeting-cloud/pfusu/time-series_forecasting_error_measures.html
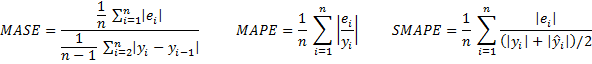
Hello Dr Zaiontz,
When evaluating forecast accuracy for seasonal data, how do we determine whether MASE or SMAPE provides a more reliable error measurement? Are there specific scenarios where one is preferred over the other?
Thanks
Hello Altama,
I don’t have an opinion about this, but the following article could be helpful:
https://robjhyndman.com/papers/foresight.pdf
Charles
Dear Dr. Zaiontz,
1. Is the coefficient of variability (Std. Deviation/Average sale) a good measure of forecast accuracy?
2. Will it be possible to demonstrate how to determine the smoothing factor (alpha) using 12-month history of original forecast versus actual sale?
Thanks.
Aftab
Hello Aftab,
1. It depends on what data set you are calculating the coefficient of variability on. Taking the coefficient of variability on the original time series is not a useful measure of forecast accuracy.
2. Which forecasting method do you have in mind? If Exponential Smoothing, this is explained on this website.
Charles
Hello Dr Zaiontz,
I’m building a proof-of-concept forecasting tool in Excel that helps our business to select the best possible model. The performance metric I would like to use is the average relative MAEs using weighted geometric mean (AvgRelMAE) (Davydenko, A., & Fildes, R. (2016))
Is this included somehow in RealStats?
Thank you,
Steven
Hello Steven,
Real Statistics will use the MSE and MAE metrics, but not the AvgRelMAE metric. You can, however, build the models as shown on the website using Solver but instead of using the MSE or MAE metric, you can use the AvgRelMAE metric.
Charles
The implementation of AvgRelMAE is straightforward:
1) create a table with the following columns:
MAE(method1) MAE(method2) …. MAE(methodN)
2) select your benchmark method (say, method1)
3) calculate RelMAEs:
RelMAE(method2)=MAE(method2)/MAE(method1)
RelMAE(method3)=MAE(method3)/MAE(method1)
…
4) calculate logs of RelMAEs, logRelMAE
5) calculate arithmetic means of logRelMAE, mean(logRelMAE)
6) calculate exp(mean(logRelMAE)) for each method
Hi DR.
Need help on RMSE values.
How can I say it’s small or not?
Compared to mean error or to what?
Is their rules to interpret RMSE?
Thanks
See
https://stats.stackexchange.com/questions/56302/what-are-good-rmse-values
http://www.theanalysisfactor.com/assessing-the-fit-of-regression-models/
Charles
For those who are interested in the topic:
This paper provides a summary of recent advances in the area of point forecast evaluation (including accuracy evaluationand forecast bias indication):
Davydenko, A., & Goodwin, P. (2021). Assessing point forecast bias across multiple time series: Measures and visual tools. International Journal of Statistics and Probability, 10(5), 46-69. https://doi.org/10.5539/ijsp.v10n5p46
The paper proposes several straightforward yet effective metrics and visualization tools that facilitate accuracy and bias assessment in datasets with multiple time series and rolling-origin forecasts. It also emphasizes the importance of using both mean and median bias measures, which help to differentiate systematic over- or under-predictions across series. The authors introduce a range of tools for cases where different loss functions are used to optimize forecasts.
The paper illustrates the approach using simple simulated datasets.
You can read it here:
https://zenodo.org/records/5525672
Andrew,
Thanks for sharing this information.
Charles