Holt-Winters Multiplicative Method

Basic Concepts

In the Holt-Winters Method (aka Triple Exponential Smoothing), we add a seasonal component to Holt’s Linear Trend Model. We explore two such models: the multiplicative seasonality model and the additive seasonality model. We consider the first of these models on this webpage. See Holt-Winters Additive Model for the second model.

Let c be the length of a seasonal cycle. Thus c = 12 for months in a year, c = 7 for days in a week, and c = 4 for quarters in a year. The model takes the following recursive form for all i > c

Holt-Winter u equation

image004z

Holt-Winter s equation

where 0 ≤ α ≤ 1, 0 ≤ β ≤ 1 and 0 ≤ γ ≤ 1.

The ui values represent the baseline, the vi values represent the trend (i.e. slope) and the si values represent the seasonality component. In the multiplicative model, for any consecutive c periods of time, the sum of the si values is approximately equal to c (at least for reasonable values of α, β, γ).

The predictions for the data elements yi can be expressed by

Predicted y values

For forecasts at future times, we use the form

Forecasted future y valueswhere h′ =INT((h–1)/c)+1.

Alternative Forms

We can also use the following alternative version of the seasonality term:

Alternative seasonality term

Based on this version of the seasonality term, we have the following alternative form of the recursive equations:

Alternative u_i term

Alternative v_i term

Alternative s_i term

Alternative y_i

The initial values for the model, i.e. where 1 ≤ i  ≤ c, are

Initial values Holt-Winters

Alternatively, we can set the initial trend value by using the average slope for the first two years, namely:

Initial trend

Note that if γ = 0, then the Holt-Winters model is equivalent to Holt’s Linear Trend Model, and if β = 0 and γ = 0, then the Holt-Winters model is equivalent to the Simple Exponential Smoothing Model.

Examples

Example 1: Calculate the forecasted values of the time series shown in range C4:C19 of Figure 1 using the Holt-Winter method with α = .5, β = .5 and γ = .5.

The result is shown in Figure 1. First, we calculate s1, s2, s3, s4, where c = 4, as shown in range F4:F7. We do this by inserting the formula =C4/AVERAGE(C$4:C$7) in cell F4, highlighting the range F4:F7, and pressing Ctrl-D.

Next, we calculate uc and vc by placing the formula =C7/F7 in cell D7 and the value 0 in cell E7.

We now insert the formula =C$22*C8/F4+(1-C$22)*(D7+E7) in cell D8, the formula =D$22*(D8-D7)+(1-D$22)*E7 in cell E8, =E$22*(C8/D8)+(1-E$22)*F4 in cell F8 and the formula =(D7+E7)*F4 in cell G8, and then highlight the range D8:F19 and press Ctrl-D.

Holt-Winters method Excel

Figure 1 – Holt-Winters Multiplicative Method

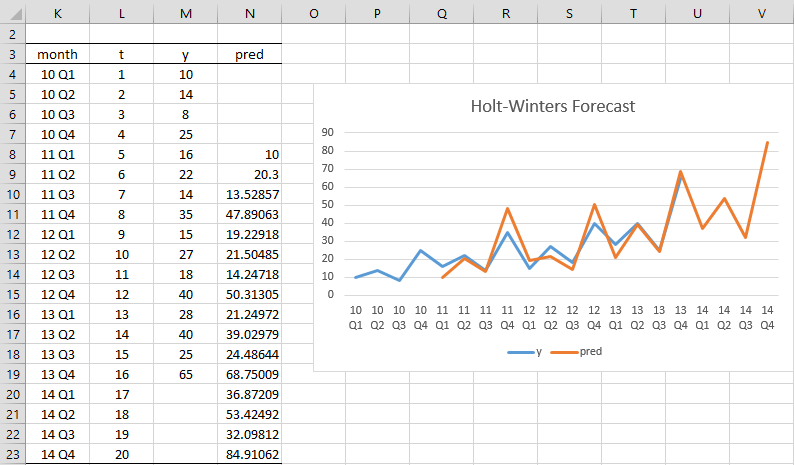
Example 2: Forecast the y values for 2014 from Example 1 (i.e. the next 4 quarters).

The result is shown in Figure 2. The values through 2013 are copied from Figure 1. The forecasted value for Q1 of 2014 is 36.87209 (cell N20), as calculated by the following formula with reference to cells in Figure 1.

=(D$19+(L20-L$19)*E$19)*F16

The other three forecasted values are calculated by highlighting the range N20:N23 and pressing Ctrl-D.

Holt-Winters forecast

Figure 2 – Holt-Winters’ Multiplicative Forecast

Optimization

As we have done in Example 2 of Holt’s Linear Trend, we can use Solver to determine which values of alpha, beta, and gamma yield the best Holt-Winters fit for the data in Example 1.

The optimization approach using Excel’s Solver, however, is susceptible to finding a local minimum instead of a global minimum. For this reason, the optimized values for alpha, beta, and gamma are sensitive to the initial values used. You can have Solver try out different initial values to find parameter values that reduce the value of MAE.

To do this, select Data > Analysis|Solver and press the Options button on the Solver dialog box. The Solver dialog box automatically contains the values collected by the Basic Forecasting data analysis tool. Now, choose the Multistart option from the GRG Nonlinear tab of the Options dialog box. Solver will now run multiple times using different starting values, picking the values that produce the best outcome. The cost of this option is slower run times.

In Real Statistics Forecasting Tools, we use a slightly different approach to improve on the optimization approach. This follows along the lines described in Holt’s Trend Confidence Interval.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

Reference

Hyndman, R. J., and Athanasopoulos, G. (2021) Holt-Winters’ seasonal method. Forecasting: principals and practice, 3rd Ed.
https://otexts.com/fpp3/holt-winters.html

119 thoughts on “Holt-Winters Multiplicative Method”

  1. Hi Charles,
    1. I have a data series of 240 EOM stock prices. I have converted this into annualised returns using the LN function which gives me in essence 240 years of return data now. Would it make sense to run a forecasting model HWA or HWM or even Arima over annualised return data instead of raw price data ? I presume the data would be stationary and no additional detrending would be necessary. Would there be any advantages in doing so ? Your opinion is much appreciated.
    2. Other than this, a great stats website you have put together. It’s been a help in many ways already. Any other means that Paypal for a donation ?
    Cheers and keep up the good work,
    Dirk
    Belgium

    Reply

    • Hello Dirk,
      1. There are many approaches for forecasting, including HWA, HWM, and Arima. I assume that your data has a trend and seasonality (otherwise you probably wouldn’t have included HWA and HWM).
      Why do you presume that your data is stationary? If it is, then probably detrending wouldn’t be necessary.
      2. Thank you very much for your kind remarks and support.
      The only approach that I have set up for donations is Paypal.
      Charles

      Reply

      • Charles,
        Thanks for your reply.
        The data indeed has a trend but no seasonality is present.
        Stationarity of the data would still have to be verified. I presume annualising this raw data over 12 periods with the LN function would make it stationary (or close to it). I’ll have a look using the ADF test just to make sure. If I want to use Arima it would have to be stationary, HWA and HWM does not really require stationarity (I presume).

        Reply

          • Charles,
            Yes indeed, HLT would be better as you say. Meanwhile I found out that annualising the price data with the LN function does not result in stationarity of the series. Differencing once does the trick. Then Arima and HWA produce adequate results, however I think forecasting would work better with the raw price data, going by the metrics.

  2. Prof. Zaiontz, this article (and the Additive Model’s article) constrains “where 0 < α ≤ 1". Did you mean to specify 0 ≤ α ≤ 1 (greater than OR equal to 0)? As required by your Resource Pack, should I add 'gamma ≥ 1 – alpha' as a constraint in Solver (when not using your Resource Pack)? Thanks.

    Reply

  3. Dear Charles,

    Thanks for this wonderful work!

    I have observed people asking about forecasting further out than c. I am using my company computer and it does not allow me to download Real Statistics Resource Pack. And therefore I have no idea how you approached forecasting further out than c in your program. Can you please elaborate further?

    I don’t know if it makes sense, but my approach was the following:
    * For the first point after c periods, we will be needing the seasonality term of the first forecasted period.
    * The seasonality term requires a Level estimation. The Level estimation requires realized values, however, given that we are now in the forecasted future, I have used the forecasted value instead of the realized value in the equation, making it become: Alpha x (Forecast / Seasonality Term of c periods ago) + (1 – Alpha) x (Level of 1 period ago + Trend of 1 period ago)
    * Coming back to the seasonality term; it is normally calculated using the realized values, however, given that we are now in the forecasted future, I have used the forecasted value instead of the realized value in the equation, making it become: Gamma x (Forecast / Level) + (1- Gamma) x (Seasonality Term of c periods ago)
    * Now I can use the seasonality term of the first forecasted value, for the calculation of the forecast value for the period, c+1 periods after the final realized data.

    Reply

  4. Hi Charles,
    I was wondering how you would forecast past the seasonal level? i.e. forecasting monthly sales, I understand how to forecast 12 months into the future by using the seasonal calculations, but how would you forecast 18 months as you ‘run out’ of seasonal data to use as it only covers 12 months into the future
    Thanks, Kade

    Reply

  6. Hello Charles Sir,
    I am doing a research project and want to use the Holt Winters Method. and I am looking for an excel sheet as an example with the Formulae (like the one whose image you have pasted in the article).
    Is it possible to send me the xcel sheet which will help me understand this better.
    I shall be highly grateful to you
    Best Regards

    Reply

    • Hell Marco,
      Yes, you are correct. I have corrected this on the website (and made a similar change for the additive version of Holt-Winters).
      Thank you very much for your help and I apologize for my delayed response to your comment.
      Charles

      Reply

  8. I cannot thank you enough for creating this explanation and downloadable examples.

    I had been relying on the wikipage (“Exponential Smoothing”), which leaves much to the imagination — and some of which seems incorrect.

    As I work through your details (WIP), I hope it is okay if I make note of some apparent inconsistencies (subject to your review) from time to time. For example….

    —–
    1. You write:

    (a) “In the multiplicative model, for any consecutive c periods of time, the sum of the si values is approximately equal to 1“.

    and

    (b) For the additive method: “The sum of the seasonality components for c consecutive periods of time is approximately c (not 1 as in the multiplicative model).“

    Errata: It appears to be c for multiplicative, as well as for additive.

    In your “Holt-Winter” worksheet (multiplicative), the average sum of “c” consecutive s[i] values is 4 (c), not 1, for the example model where c=4 and alpha=beta=gamma=0.5.

    In fact, the average sum rounds to 4 (c) in 89% of 1000 trials with random alpha, beta and gamma (gamma <= 1-alpha).

    And I have not seen 1. The min average sum rounds to 4.

    —–
    2. OTOH, the max average sum of s[i] values rounds to 6.70 when alpha=0.003092692913089, beta=0.718335362652918 and gamma=0.934268804623004 in the "Holt-Winter" worksheet (multiplicative).

    And the relative sd is large, with min sum of s[i]=4.39 and max sum of s[i]=10.2.

    So, I wonder if it would be helpful to add limits on the expected average sum of s[i] values as additional criteria for finding a "good" set of alpha, beta and gamma. For example, C22:E22=3.5 for c=4.

    And I wonder if it would be helpful to add similar limits on the min and max sum of s[i] values, as well. For example, both must be between 3.5 and 4.5 for c=4.

    Reply

    • Hi Joe,
      Sorry for the late response.
      Yes, you are correct. I have modified the webpage to reflect this.
      Thank you very much for identifying this error and for improving the accuracy and useability of the website.
      Charles

      Reply

  9. Dear Charles,
    this site is really helpful.
    Great explanation in this webpage and the Add-Ins for Excel.

    Is it possible to find another Add-Ins for Excel that includes Holt Winters with application of Nelder Mead method for coefficients optimization?

    Reply

    • Dear Riccardo,
      That is indeed a good idea since Solver doesn’t always find the optimum coefficients.
      I will consider using Nelder Mead, although I have been thinking about using a different approach.
      Charles

      Reply

  10. Dear Charles,

    thank you very much for this webpage and the Add-Ins for Excel. I am trying them out at the moment and I have a few questions:

    – Why is it necessary that Alpha + Gamma is smaller than or equal to 1? And why is it – using Solver – mostly exactly equal to 1? I have read the Wikipedia Page about Exponential Smoothing and there is no such condition.

    – How is the best way to choose the parameters yourself? Is it always best to minimize some kind of error or are there other methods? Do you know with which method they are chosen in the excel forecast function forecast.ets? Or is there some possibility to choose it yourself?

    Thank you very much in advance!
    Janne

    Reply

  11. Dear Charles,

    First of all, thank you very much for your article, its truly great and easy to understand.
    I have tried to use the learned on own dataset but faced some issues when forecasting, namely forecast quickly tends to negative values instead of following the normal trend. It is a dataset with 24h periodicity with Gaussian like distribution / day with peaks between 10h-14h (traffic statistics).
    I have 1390 historical rows (~58 days, 2 rows are missing actually) where last known ‘u’ and ‘v’ values calculated from historical data are:
    u_1390 = 1.07546
    v_1390 = -0.16529
    As ‘s’ is always positive, pred = (u_1390 + (t – 1390) * v_1390) * s_1368 equation quickly leads to a decreasing trend after t = 1391, 1392, etc. where increasing periods do not “come back” at all.
    Used formulas are correct, I have checked with your data and everything fits your results. Prediction on historical data is also OK with my dataset but forecast fails.
    Unfortunately I cannot upload file or screenshot but I would be happy to send you by e-mail.

    Could you please check what could be a problem? Is it possible that HW method is not applicable for such dataset?

    Thank you very much in advance,
    All the best,
    Tamas

    Reply

  12. Hi Charles,
    What is the logic behind forcing α and β to be less than 1 ?

    In most forecasting models I have seen, this is not really necessary.

    Thanks
    Murad

    Reply

    • Murad,
      These are weights. Think of alpha as dividing 1 into alpha and 1-alpha. Similarly for beta.
      You said that in most forecasting models these restrictions are not necessary. Can you give me a reference to one such model or give me an example where the values of alpha and beta are not between 0 and 1?
      Charles

      Reply

  14. Dear Charles, thank you very much for your article.

    I would like to ask kindly a question: I have data which shows clearly a negative trend (T-Test confirms) . I deseasonalized the data to get the initial level and trend estimates via a trendline on the deseasonalized series. The initial values for the trend (-0.7) is negative. Now using Solver in Excel, yields for the trend smoothing parameter simply 0 because I set the constraint that only values between 0 and 1 are allowed. If data shows a negative trend is it correct if the solver is simply puts the trend smoothing parameter to 0 and the model continues to calculate with the initial trend value (-0.7) ?

    Best Regards,
    Nic

    Reply

      • Hi Charles,

        Thank you for your reply, it is very much appreciated. Initially I thought the data would yield a positive trend, not negative. Hence I did not adjust the constraints of smoothing parameters. If the data shows a negative trend, I can/should lower the solver constraint regarding the trend smoothing parameter to -1?

        Best Regards,
        Nicolas

        Reply

    • Murad,
      I know that Solver doesn’t always find the global optimum parameter value and can instead find a local optimum value.
      I don’t know whether it results in overfitting.
      Charles

      Reply

  16. Hello Mr Charles, thanks for this great explanation. However when I tried to forecast for the next quarters on my own, if observed that the (Si+h-ch’) should be 14 instead of 13 used on this page because I got the value of (h’) to be 1. I hope I am not mistaken.
    Thanks in advance!

    Reply

  17. Hello,
    Can someone please help me solve Holt’s model by hand using a multiplicative trend or even tell me a page in which I can find examples because I’m having it hard to find a page which explains these examples without excel, this are the information I have:

    Assume you are working with monthly data, with December being month
    12, January being month 13 etc. Suppose L12 = 80 and T12 = 1.2 and you
    observe Y13 = 90. Determine the forecast for Y15, assuming α = 0.3 and
    β = 0.7 using a multiplicative trend.

    Thank you in advance.

    Reply

  20. Dear Sir,
    Your explanations are so clear. I understand there are various methods to attain the starting values in HW. Pls share whose method you have used here. does the initial values are deseasonalised? Thank You

    Reply

  21. Hey Charles,

    thanks for putting this site together!
    Is there a way to set a “floor” with Holt Winters? For instance, if sales trends have been negative for a long time the forecast continues to be negative and predicting a monthly forecast beyond 4-6 months starts to produce unrealistic (less than zero) results. Is there a way to set a minimum threshold that prediction cannot go below?

    Thanks

    Reply

  22. Hi Charles,

    I have followed your method and the final alpha, beta and gamma values provided to me by the Solver are dependent on the initial values alpha, beta and gamma values I input.
    Is that supposed to happen?

    For example: If I have 0.5 as my initial alpha, beta and gamma values, Solver gives me alpha = 0.46, beta = 0.5 and gamma = 0.54.
    Whereas, If I have 0.6 as my initial alpha, beta and gamma values, Solver gives me alpha = 0.48, beta = 0.6 and gamma = 0.48.

    P.S. I have set my objective in the Solver to minimize MAE

    Reply

    • Hello Yash,
      In general, it is possible that the results will depend on the initial parameter values. Whether or not this is so for this situation, I can’t say. If you send me an Excel file with your data, I will give you a more precise answer.
      Charles

      Reply

  23. Note in this excellent excel implementation the seasonality includes the term y(i)/u(i), rather than y(i)/(u(i-1)+v(i-1)) as shown in https://otexts.com/fpp2/holt-winters.html (1)

    A hasty check suggests this isn’t critical. But when implementing Holt-Winters’ damped method (1) then I *think* the original equation is easier to work with.

    (1) Hyndman, R.J., & Athanasopoulos, G. (2018) Forecasting: principles and practice, 2nd edition, OTexts: Melbourne, Australia. OTexts.com/fpp2. Accessed on 23 Jun 2019

    Reply

      • Hi Charles,
        Hyndman appears to reference this point: “In many books, the seasonal equation…is slightly different from these, but I prefer the version above because it makes it easier to write the system in state space form. In practice, the modified form makes very little difference to the forecasts.”

        https://robjhyndman.com/hyndsight/hw-initialization/

        So I believe the equations you used are the original form which ‘m sure you already knew. I’m just happy knowing that my loose end was conveniently resolved.

        Reply

  24. Hello,
    Do you know if there is a specific scale of judgement of forecast accuracy for the Error measures you used? In this case MAE and MSE. How can you tell if your obtained error is adequate, too small or too big. (for both error measures)
    Thank you in advance for answering.

    Reply

    • Hello Clark,
      There is no simple answer to this question. The smaller MSE (or MAE) the better. Thus if you have two models, one with MSE of 10 and the other MSE of 9, then all other things being equal, you prefer the one that has MSE equal to 9.
      Ideally you should build your model with part of the data and then test to see how good your model does with the rest of the data (where you already know the correct forecast values (namely the actual values). This is called cross validation.
      Charles

      Reply

      • Thanks for your response. May I ask why you chose the additive over the multiplicative? I also read that there are various ways to initialize the Winter Holt’s method. Can you explain the pros and cons of each type?

        Reply

    • Hello Tamika,
      I looked into this further and see that the info I gave you previously was wrong. I seem to be using a multiplicative model, but it seems to be a little different from the standard model. As a result, I plan to investigate this further and if necessary change it to the standard model in the next release. I will also include both the additive and multiplicative models. I hope to have this available in the next few days.
      Thanks for raising this issue.
      Charles

      Reply

    • Tamika,
      I have now looked into this further, and found that the approach I used was the standard approach, although I plan to change the initial values in the next release. I will also correct the forecast values for the data, which will change the optimized values. Finally, I will also add the additive version.
      Charles

      Reply

      • Thank you Charles for this information. The wealth of knowledge that you are providing is appreciated. May I ask if your Real Statistics add-in can be used for Data Mining?

        Reply

  26. HEY,
    i have some questions for how to choose the period , here is my question
    1) if i have 1 year of daily data means it is 365 entries (it’s not a leap year) So period is 364
    now
    2) if it is leap year means 366 entries , now what is the period ?? because 365 gives a wrong forecast
    3)why exponential smoothing is not taking 364 while total num of data is 366?
    4) ExponentialSmoothing(dataframe ,seasonal_periods=period ,trend=trend,damped=True , seasonal=seasonal) this syntax i am using
    5) but if we have two year of data like (365+366) or (365+365) then period 364 gives a expected output
    help will be appreciated
    thanks

    Reply

    • Hello,
      1. The period is 365, but unless you are going to look at trends from a specific day (e.g. Jan 4) or days from year to year, there is no point in taking seasonality into account. In this case, you might as well use the Holt’s Linear Trend model.
      2. 366, but see response to #1.
      3. I don’t understand what you mean by “…is not taking 364”.
      4. I don’t know which software package you are referring to.
      Charles

      Reply

  27. Goedemiddag,

    Ik heb een vraag:
    Ik werk in een productie organisatie en wil de forecast optimaliseren.

    Mijn vraag/stelling is als volgt:
    Huidige week = 4. (maandag!) De afzet van week 4 is dan niet niet totaal bekend.
    Plannen voor = week 5
    Afzet = week 6.

    Hoe kan ik tijdig de forecast aanpassen voor week 5(productieweek) o.b.v. historische data (Moving Avarage).
    En hoe kan ik deze trend doortrekken naar week 6,7,8,9,10 enz. als ik nog niet op de hoogte ben van de werkelijke afzet in deze weken ?

    Reply

    • Hello Daniel,
      These types of forecasting issues are not so easy to solve. These sorts of issues are more art than science and are not easy to answer quickly.
      I suggest that you try different forecasting models holding out some of the data so that you can evaluate the accuracy of each model based on the real data that you held out.
      Charles

      Reply

  28. Hi Charles

    Great work!

    I just wonder why Excel 2016’s ETS (exponential triple smoothing) forecast function
    =FORECAST.ETS provides another result than yours Holt-Winters forecast.

    Thanks.

    Reply

    • Hi Alex,
      Can you send me an Excel file with your data and the results you obtained from the FORECAST.ETS function? I will try to figure out why you are getting different results. There a number of different implementations of ETS/Holt-Winters and so Real Statistics may be using a version different from the one chosen by Microsoft.
      Charles

      Reply

    • Excel ETS can result in a very spiky FC fit at times for no apparent reason. Holt-Winters (add) performs better in my opinion.

      Reply

  29. I stumbled upon this page whilst researching how SAP APO Statistical Forecast models were generating their Basic, Seasonal, Trend values. After reading so many articles that talk theory only this is a fantastic practical example which actually clearly demonstrates the calculations. Thanks so much for putting this together.

    Reply

  30. Hey Charles

    Thanks a million for this. Please can you specify how do you calculate the rest of seasonal indices after 10 Q4?

    Reply

    • Fahad,
      Suppose you want to forecast one more year (11 Q1, 11 Q2, 11 Q3, 11 Q4). One approach is to copy the range L23:N23 into the range L24:N24. L24 should contain the value 20 and N24 should contain the formula =(D$19+(L24-L$19)*E$19)*F20. Now replace F20 by F16 in this formula (the latest estimate for Q1). Next highlight the range L24:N27 and press Ctrl-D.
      Charles

      Reply

  32. Hi Charles,
    Could you please advise the logic behind γ factor should be less than 1–α (aka γ < 1–α) ?
    My understanding γ value can be in the range of 0 – 1.00.
    Thank you in advance!

    Reply

  33. This site is really helpful and the example is a godsend!
    One question. Shouldn’t, in equation 1, the variable w sub(i-c) in the equation for u sub i,
    be the variable s sub (i-c)?
    Also,
    shouldn’t in equation 3 be S sub i instead of w sub i?

    Peter

    Reply

    • Peter,
      You are absolutely correct. Thank you very much for identifying this error. At one time I used the symbol w instead of s, but forgot to change it in all places. I have now corrected the error.
      I appreciate your help in improving the website and making it easier for people to understand what is going on.
      Charles

      Reply

  34. Hi Charles,
    Great explanation. .. as I followed your example, I noticed the moving sum of the new calculated s over C periods is no longer equal to C or averaging to 1. How important is it to normalize C as we use Holt Winter model?

    I reworked the example using normalized s figures, and the MSE improved to 34.53; however, MAPE deteriorated from 17.91% to 18.22%.

    I appreciate your view on this.

    Thanks.

    Reply

    • Ayman,
      This true for the first year since that is how the values are initiated. After the first year it is not necessary for any consecutive 4 quarter period to average to 1.0. In fact it would be impossible unless all the quarter 1 values are the same, and similarly for Q2, Q3 and Q4.
      Charles

      Reply

  35. Awesome, thank you!

    However I do have a question, and I cannot find the answer in any of the tutorials.
    It’s a simple question probably everyone will encounter:
    How do I forecast for more than one season?
    Assume that I’m using the Additive model, my daily data shows a strong weekly recurrence, usually when we predict for the next season(week) we fix the level and trend components of the last day of previous week and use the seasonal component of the same weekday of last week. But what shall I do if I want to forecast more than 1 week?

    Thank you!

    Reply

  36. Dear Charles,

    I replicated your model, then applied “=FORECAST.ETS” function (as well as “Forecast Sheet” in the Data Tab, which uses the same “ETS AAA” algorithm). ETS AAA Excel algorithm is stated to implement Holt-Winters method.

    The first issue is that ETS AAA choses alpha, beta and gamma, which are 0.251 / 0.001 / 0.001 respectively for your example data. These Excel algorythm values of α, β, γ are even worse than your initial 0.5/ 0.5 / 0.5 in terms of MSE (Excel figures worsened the error by around 8 points).

    The second issue is that even if we accept 0.251 / 0.001 / 0.001 for α, β, γ, the predictions are different:

    * in your model the predictions are as follows (decimals are shortened but not rounded):
    24,7 for period #17
    34,6 for period #18
    19,8 for period #19
    61,9 for period #20

    * Excel’s ETS AAA (claimed to be Holt-Winters) algorithm predicts:
    38,5 for period #17
    47,3 for period #18
    41,2 for period #19
    60,3 for period #20

    To sum up, my ultimate concerns are rather simple: “Can we securely use Excel’s “=FORECAST.ETS” function, believing it is backed by established Holt-Winters method? Otherwise, should we avoid using Excel’s ETS AAA, for we don’t understand the calculations behind this ‘black box’ algorythm?”

    Thank you

    Reply

  37. Great explanation but is it possible to use Winter’s model to forecast farther out than c observations (4 in this case)? What ways are their to forecast say for 2015 or 2016 in this example?

    Reply

  38. very nice, just need a clarification, for prediction the formula is =(D$18+(L20-L$19)*E$18)*F16, why D$18 and E$18 NOT D$19 E$19 as, it predicts the value of 20.

    Reply

    • Debadrita Panda,
      You are correct. Thank you very much for identifying this error. I have now corrected the error on the referenced webpage.
      I really appreciate your help in improving the Real Statistics website.
      Charles

      Reply

  39. Hi Charles,
    Thanks for the help.

    If the time series data has y=0 as some entry the calculation for S and u, v start giving DIV#0 error. If i replace 0 with a very small number like 0.001 the value for initial S goes very low and value of u,v gets multiplied by same factor and the forecast has huge errors.
    Sample Data : YEAR Month mm
    2012 Jan 16.7
    2012 Feb 0
    2012 Mar 0
    2012 Apr 8.2
    2012 May 0
    2012 Jun 2.1
    2012 Jul 438.4
    2012 Aug 367.6
    2012 Sep 71.5
    2012 Oct 0
    2012 Nov 0
    2012 Dec 0

    What do you suggest can be done?

    Reply

Leave a Comment